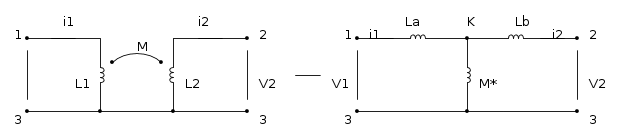Indice |
Presentazione
Salve a tutti, volevo utilizzare il mio primo articolo per condividere le mie conoscenze (seppur non molto estese) riguardo ad un argomento del quale non sono riuscito a trovare molto in rete: le trasformazioni a "T" e a "π" delle mutue induttanze, un argomento trattato un un post qualche settimana fa! Per fare questo, mi servirò di alcuni esercizi affrontati nel mio percorso universitario (ancora da completare)!
Introduzione
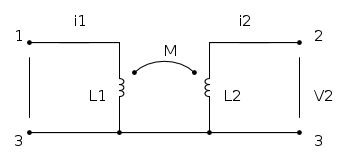
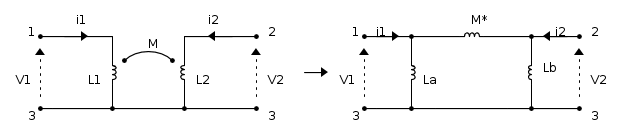
Si considerino due induttanze accoppiate mutuamente tra loro come nel seguente schema:
si può notare che il terminale 3 è in comune alle due induttanze e quindi si trova allo stesso potenziale. Le due trasformazioni possibili (a "T" e a "π") ci permettono di avere un circuito senza accoppiamenti magnetici tra le induttanze. Queste trasformazioni sono estremamente utili per l'applicazione del METODO DELLE TENSIONI NODALI, o per esempio per facilitare lo studio di circuiti magnetici.
Trasformazione a "T"
In questa trasformazione, come si può notare, si va ad aggiungere un nuovo nodo alla rete, il nodo K, mentre i nuovi valori delle induttanze si possono calcolare tramite la relazione costitutiva delle mute induttanze, e sono:



dove il segno dipende dalla posizione dei "contrassegni" delle induttanze nel circuito originale:
- Si sceglie il segno "sopra" se i contrassegni sono concordi al nodo equipotenziale (tutti e due rivolti dalla parte del nodo in comune, o tutti e due rivolti dalla parte opposta al nodo in comune)
- Si sceglie il segno "sotto" se i contrassegni sono discordi al nodo equipotenziale (uno "confinante" col nodo in comune e l'altro opposto allo stesso)
vediamo un esempio
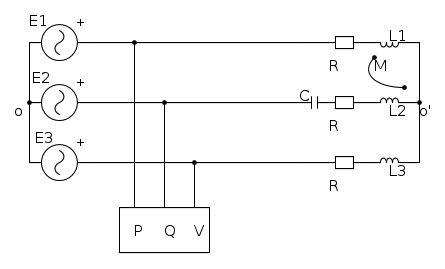
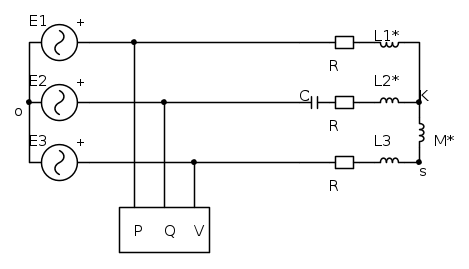
Il sistema trifase in figura è alimentato da una terna SIMMETRICA DIRETTA di valore concatenato (efficace) pari a  e frequenza
e frequenza  . Si chiede di determinare la potenza ATTIVA, REATTIVA ed APPARENTE erogata dal generatore e la tensione Vs (ovvero la differenza di potenziale tra i due centri stella) in valore efficace.
I dati del problema sono:
. Si chiede di determinare la potenza ATTIVA, REATTIVA ed APPARENTE erogata dal generatore e la tensione Vs (ovvero la differenza di potenziale tra i due centri stella) in valore efficace.
I dati del problema sono:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
Svolgimento
Come prima cosa ci andiamo a calcolare l'impedenza del carico, servendosi dei dati di targa, forniti nei dati del problema. Quindi procediamo calcolandoci come prima cosa la CORRENTE NOMINALE del carico e successivamente usandola per calcolarne l'impedenza:

dove

infine




Notiamo che la REATTANZA risulta negativa, perché essendo la potenza nominale REATTIVA del carico negativa, ci fa capire che si tratta di una carico Ohmico-Capacitivo
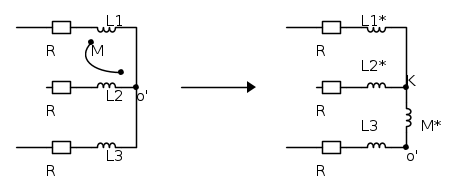
Adesso arriviamo al dunque, alla "famigerata" trasformazione a "T": possiamo trasformare il mutuo accoppiamento che "lega" la linea 1 e la linea 2 in questo modo
e i nuovi valori delle induttanze diventano:



dove si è scelto il segno "sotto" perché i contrassegni erano opposti al nodo equipotenziale.
N.B. Bisogna fare attenzione al ri-posizionamento del nodo s e del nuovo nodo K: il primo "slitta" tra M * e L3, mentre il nodo K diventa il nuovo CENTRO STELLA a fine linea!!
A questo punto ci possiamo calcolare le impedenze equivalenti delle 3 linee:




UDITE UDITE... il problema si riduce allo studio di un sistema trifase SIMMETRICO ed EQUILIBRATO, cosa impensabile (per lo meno ad un occhio inesperto come il mio) vedendo il circuito iniziale!!
Come se non bastasse, andando a fare il parallelo tra i due carichi, ci accorgiamo che il circuito diventa PURAMENTE RESISTIVO, perché il carico Ohmico-Capacitivo va a rifasare completamente il carico a fondo linea:
 quindi
quindi 
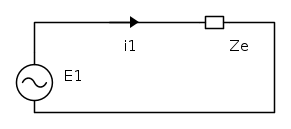
Adesso, si possono ricavare le correnti di linea studiando il circuito monofase equivalente:



Ricordandoci che  Per calcolarci le potenze (ATTIVA, REATTIVA ed APPARENTE) erogate dal generatore, possiamo calcolare la potenza complessa dello stesso:
Per calcolarci le potenze (ATTIVA, REATTIVA ed APPARENTE) erogate dal generatore, possiamo calcolare la potenza complessa dello stesso:

dalla quale si ricavano:



Per l'ultimo passaggio del problema ci ricaviamo la corrente nel carico a fondo linea con un partitore di corrente:




infine, utilizziamo la legge di Ohm per calcolare la tensione Vs:


La tensione VK è la differenza di potenziale tra i due centri stella del "nuovo" circuito ed è nulla, perchè si tratta di un sistema SIMMETRICO ed EQUILIBRATO, quindi la tensione tra i due centri stella è nulla perchè questi sono allo stesso potenziale!!
La risoluzione di questo problema è stata semplificata notevolmente dall'utilizzo della trasformazione a "T", che ci ha permesso di studiare una rete trifase, all'apparenza "difficile", rendendola SIMMETRICA ed EQUILIBRATA.
Trasformazione a "π"
Nel caso della trasformazione a "π", si va ad aggiungere una nuova maglia alla rete. I nuovi valori delle induttanze risultano essere:



con Δ = L1L2 − M2
Anche per questa trasformazione, si segni si "scelgono" con le considerazioni fatte per la trasformazione a "T"!!
- N.B.Affinché sussista l’equivalenza si deve imporre che l’impedenza operazionale vista da dueterminali corrispondenti, sia uguale per i due circuiti, quello originale e quello trasformato, ma vi ho risparmiato i calcoli (non sono difficili, ma sono abbastanza)!!
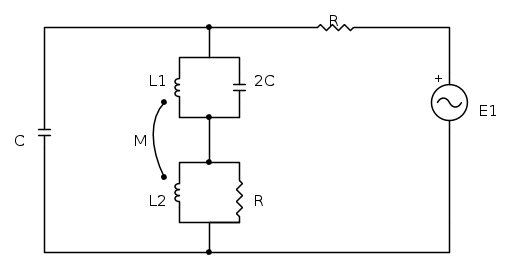
Vediamo un esempio:
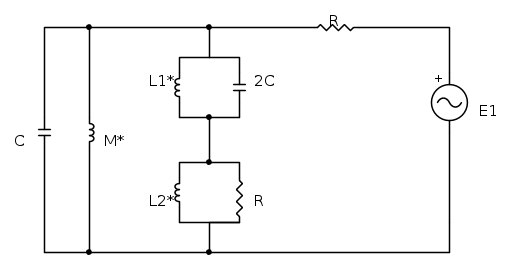
Questo circuito deriva dallo studio di un circuito magnetico, del quale ho preso solamente il generatore sinusoidale. I dati del problema sono:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
Il problema richiede di calcolare l'energia media immagazzinata nel nucleo magnetico, ovvero nelle induttanze mutuamente accoppiate. Per fare questo, ci serve calcolare la corrente che attraversa il mutuo accoppiamento. Notiamo subito che le due induttanze hanno un terminale in comune, quindi possiamo trasformarle, e in questo caso la trasformazione più conveniente è quella a "π":
con i nuovi valori delle induttanze (scegliendo il segno "sopra" perché hanno i contrassegni concordi):



Adesso notiamo che ci sono due rami paralleli "sospetti": il ramo  e quello M * − C, che potrebbero essere dei rami RISONANTI, quindi procediamo calcolandoci la pulsazione di risonanza di entrambi i rami:
e quello M * − C, che potrebbero essere dei rami RISONANTI, quindi procediamo calcolandoci la pulsazione di risonanza di entrambi i rami:


quindi entrambi i rami risultano essere dei rami RISONANTI PARALLELI, che si comportano come dei rami APERTI. Quindi si conclude il problema calcolando l'energia immagazzinata nei rami risonanti paralleli con l'apposita formula.
Anche in questo problema, la trasformazione del mutuo accoppiamento ci ha permesso di sbrogliare un problema, non molto complesso, ma sicuramente ricco di calcoli, che spesso portano ad errori (oltre che a perdita di tempo inutile durante un esame)!!
Conclusioni
Spero che questo articolo sia, prima di tutto corretto (hihihihi) e in secondo luogo utile a chiunque abbia bisogno di alcune delucidazioni riguardo all'argomento trattato!! Infine vorrei ringraziare Admin per avermi dato qualche consiglio per la stesura dell'articolo e tutti quelli che hanno partecipato al Topic sulle trasformazioni delle mutue induttanze RenzoDF e Pando!!
PS Mi scuso per la formattazione, ma ricordo che è il mio primo articolo, quindi spero non sia nemmeno troppo "scarsa".
PPS commentate pure, anche criticando (spero in modo costruttivo), perchè per me sarebbe molto utile!!

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)