Indice |
Abstract
Nei due precedenti articoli (1 e 2) si è visto che per schematizzare una linea di trasmissione è necessario conoscerne le costanti fondamentali.
Sono la resistenza r, la reattanza x, la suscettanza b e la conduttanza g per unità di lunghezza.
In questo si vedrà come calcolarle, sia per linee aeree che in cavo. I costruttori di cavi, ed anche di corde nude, ne forniscono in genere il valore; occorre però ricordare che esso è riferito alla configurazione geometrica, specificata dal costruttore.
resistenza chilometrica: 
linee aeree
La resistenza chilometrica è proporzionale al rapporto tra la resistività ρ del materiale (rame o alluminio) che dipende dalla temperatura, e la sua sezione S. Quindi, a 20 °C si può porre
![r_{20} = K \frac{\rho_{20} }{S} \quad [1]](/mediawiki/images/math/0/0/3/00381376b195c9ca76e0f767ab67f6e3.png)

 è un coefficiente di maggiorazione per tenere conto:
è un coefficiente di maggiorazione per tenere conto:
- della maggiore lunghezza del conduttore rispetto alla lunghezza topografica;
- di perdite aggiuntive nelle giunzioni;
- dell'effetto pelle;
- delle perdite per isteresi e correnti parassite nell'eventuale anima in acciaio.
Nel caso di conduttori a fascio (vedi paragrafo successivo) la sezione da considerare è la somma delle sezioni dei conduttori che costituiscono il fascio.
Si deve poi tenere in conto la dipendenza dalla temperatura
![\begin{array}{l}
{{\rm{r}}_\vartheta } = {r_{20}}\left[ {1 + \alpha \left( {\vartheta - 20} \right)} \right]\\
{\alpha _{Cu}} = 0{,}0039 \, ^\circ {{\rm{C}}^{ - 1}};{\alpha _{Al}} = 0{,}0040 \, ^\circ {{\rm{C}}^{ - 1}}
\end{array}](/mediawiki/images/math/b/3/e/b3e608ff09264bacb8f4b685562d2c28.png)
I costruttori ne forniscono il valore per diverse temperature, come si può vedere ad esempio nel foglio dati della corda 3M ACCR, riportato nel paragrafo finale sui Dati tecnici.
cavi
anche per i cavi vale una formula simile a quella per le linee aeree con un K che tiene conto della cordatura e dell'effetto pelle.
Sono però da contabilizzare anche le perdite addizionali negli schermi. Gli schermi sono sede di forza elettromotrice indotta dalla corrente nelle fasi. Se sono aperti ad un'estremità, non sono percorsi da corrente, quindi non influiscono sul valore delle costanti. Se però si chiudono in corto da entrambi i lati, la fem indotta fa circolare correnti che dipendono dalla resistenza degli schermi. Aumentano complessivamente le perdite per effetto Joule e tutto avviene come se la resistenza dei conduttori aumentasse del  .
.
La messa in cortocircuito degli schermi può essere fatta per diminuire la reattanza (vedi paragrafo successivo) dei conduttori del  .
.
reattanza chilometrica: 
E' calcolabile con la formula
![x = \omega \left( {\frac{{{l_i}}}{n} + 0{,}46\log \frac{{2D}}{{{d_{eq}}}}} \right)10^{-3} \quad [2]](/mediawiki/images/math/a/4/3/a43a87be91c50af5d77a1ef80c061e6a.png)
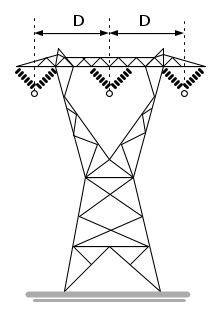
dove, indicando con Dij la distanza tra i conduttori i e j
![D = \sqrt[3]{{{D_{12}}{D_{13}}{D_{23}}}}](/mediawiki/images/math/f/9/9/f99adcb9fbb93dc3a98be7ce68cad4be.png)
è la media geometrica delle distanze e
![{d_{eq}} = 2R\sqrt[n]{{\frac{{nr}}{R}}}](/mediawiki/images/math/f/c/2/fc2a567e38fe3ec582c8d79acd2fbd53.png)
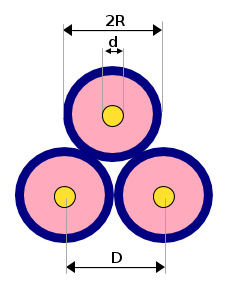
è il diametro equivalente quando una fase è suddivisa in un fascio di n conduttori ciascuno di raggio r disposti su una circonferenza di raggio R, come mostrato in figura e la terna di conduttori è simmetricamente disposta ed opportunamente trasposta (scambio regolare della posizione delle fasi)
- se il conduttore è unico ed

- Il fascio di conduttori è in genere usato per linee a 380 kV
li è l'induttanza corrispondente al flusso magnetico interno al conduttore. Se la densità di corrente è uniforme si assume
- li = 0,05 per conduttori in rame o alluminio o lega di alluminio
- li = 0,033 per conduttori alluminio acciaio.
Da osservare che esso vale zero se la resistività è nulla. In tal caso infatti la corrente è completamente superficiale, come se il conduttore fosse cavo ed all'interno non esiste campo magnetico.
Il flusso interno fa variare la reattanza dall'1% al 4%.
In base alla [2] si ha il seguente grafico
Si può anche scrivere in modo più compatto la [2] modificando l'argomento del logaritmo per tenere conto del flusso interno. Introducendo il concetto di diametro equivalente, indicato con 2δ, come il valore che deve soddisfare all'uguaglianza

si ottiene
 per cui si può porre
per cui si può porre
 (detto raggio geometrico medio) con
(detto raggio geometrico medio) con

- Se il conduttore è unico e la sezione è piena, in rame o alluminio si ha

- Se la sezione è cava k = 1
La [2] diventa dunque
![x = \omega \left( {0,46\log \frac{D}{\delta }} \right) \quad [2.a]](/mediawiki/images/math/7/0/9/7099959506c32d1a101a2e24d8a190a1.png)
cui corrisponde, alla frequenza di 50 Hz, il grafico (che in pratica è il precedente: cambia solo il modo di calcolare l'ascissa)
- Nota: per la reattanza a 60 Hz, basta moltiplicare i valori del grafico per 1,2
Il costruttore può fornire la reattanza riferita ad una data configurazione geometrica dei conduttori. Nel caso della corda ACCR della 3M, la distanza tra i conduttori disposti ai vertici di un triangolo equilatero è di  . Fornisce anche il raggio geometrico medio (geometric mean radius).
. Fornisce anche il raggio geometrico medio (geometric mean radius).
Se consideriamo ad esempio la corda Hawk 477TW il valore, a 60 Hz, è  .
.
Applicando la formula con  quindi
quindi  otteniamo infatti
otteniamo infatti
 .
.
A 50 Hz è  rilevabile anche dal grafico ovviamente.
rilevabile anche dal grafico ovviamente.
cavi unipolari
Schermi non cortocircuitati
Se gli schermi dei cavi non sono cortocircuitati, si possono utilizzare le stesse formule delle linee aeree.
I valori di reattanza sono inferiori a quelli delle linee aeree in quanto la distanza tra i conduttori è molto minore. Generalmente i costruttori forniscono il valore dell'induttanza di esercizio per una ideale disposizione a trifoglio, dove i conduttori sono al vertice di un triangolo equilatero di lato pari al diametro complessivo del cavo.
Se si dispongono in piano su userà la media geometrica delle distanze e la reattanza aumenta rispetto alla disposizione ideale, come per le linee aeree
Esempio
Consideriamo il cavo di sezione 
Il diametro del conduttore è  , mentre
, mentre  è il diametro complessivo del cavo. Si ha
è il diametro complessivo del cavo. Si ha


che è molto simile a quello fornito
schermi cortocircuitati
Se gli schermi dei cavi sono cortocircuitati, come già è stato detto a proposito della resistenza, le reattanze di esercizio diminuiscono, mentre la resistenza apparente aumenta.
![m = 0,46\log \frac{D}{R} \quad [2.a]](/mediawiki/images/math/d/2/b/d2bcbd8ebb9dbb7af921ca786098c46a.png)
dove R è il raggio dello schermo e D la distanza tra i conduttori, si ha una diminuzione della reattanza
![{x^{\prime}} = x - \frac{{{{\left( {\omega m} \right)}^3}}}{{r_s^2 + {{\left( {\omega m} \right)}^2}}} \quad [2.c]](/mediawiki/images/math/a/9/1/a919b1bef1da4937955faee66539a0d3.png)
ed un aumento della resistenza
![{r^{\prime}} = r + \frac{{{r_s}{{\left( {\omega m} \right)}^2}}}{{r_s^2 + {{\left( {\omega m} \right)}^2}}} \quad [2.d]](/mediawiki/images/math/5/6/7/567bebcf32821f42ca3ec1a1c24b5869.png)
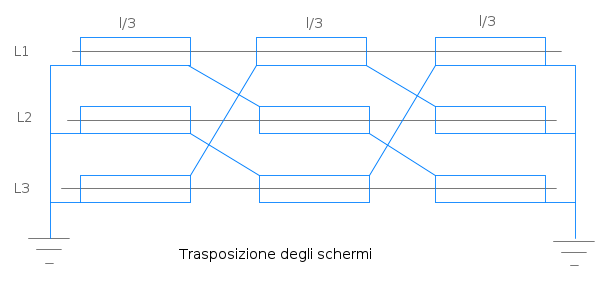
- Per ridurre le perdite, in linee lunghe si tagliano gli schermi e si incrociano i loro collegamenti in modo che in ognuno sia indotta una corrente dovuta alla somma delle correnti indotte delle tre fasi: se le correnti sono equilibrate, la corrente indotta nello schermo è nulla.
- NB: per cavi disposti a trifoglio
 è poco maggiore di 2.
è poco maggiore di 2.
cavi tripolari
In questo caso le condizioni dello schermo non influiscono in pratica sulla reattanza per cui si può usare la solita formula, in mancanza del dato fornito dal costruttore. La resistenza apparente del conduttore può aumentare del  .
.
suscettanza chilometrica: 
linee aeree
la suscettanza di esercizio è determinata dalla capacità tra i conduttori e tra i conduttori e terra, ma la capacità verso terra non influisce molto sul suo valore ed in prima approssimazione può essere trascurata. Per le linee aeree si può calcolare con
![b = \omega \frac{{24{,}14}}{{\log \frac{{2D}}{{{d_{eq}}}}}} \times {10^{ - 9}} \quad [3]](/mediawiki/images/math/f/a/7/fa7a324732a8f2b322c57943dedf8703.png)
con il solito significato dei simboli D e deq.
linee in cavo
Anche questo parametro è in genere fornito dal costruttore nel caso dei cavi.
Per cavi unipolari con schermo vale la formula vista per le linee aeree dove però compare la costante dielettrica relativa dell'isolante (per l'aria la costante dielettrica relativa è uguale ad 1) e la distanza D che si considera è in pratica il raggio interno dello schermo R. Quindi, indicando con r il raggio del conduttore si pone
D = R e deq / 2 = r
![b = \omega \frac{24{,}14 \epsilon_r }{\log \frac R r} \times {10^{ - 9}} \quad [3.a]](/mediawiki/images/math/1/d/b/1db60b44029dafd07e659f4e774c93a0.png)
La costante dielettrica relativa vale
 per carta impregnata
per carta impregnata
 per il polietilene
per il polietilene
- εr = 4 per la gomma butilica
Per i cavi tripolari con unico schermo è bene riferirsi al dato del costruttore. Una formula utilizzabile è comunque
![b = \omega \frac{{24{\epsilon _r}}}{{\log \left( {2{,}66\frac{s}{d} + 1} \right)}}{10^{ - 9}}\frac{{\rm{S}}}{{{\rm{km}}}} \quad [4]](/mediawiki/images/math/1/a/b/1abd4f0424720c17881044d83dd8c111.png)
dove d è il diametro del conduttore ed s lo spessore dell'isolante tra conduttore e schermo.
conduttanza chilometrica 
linee aeree
tiene conto dell'effetto corona e di altre perdite negli isolatori. Generalmente si valutano tali perdite globalmente, per fase e per chilometro, ed indicando con p tale perdita in kW e con E il valore efficace della tesione stellata in kV, si ha
![g=\frac{p}{E^2} \quad \text{mS/km} \quad [5]](/mediawiki/images/math/9/9/1/9917ea8de2ccf1d2087b38225e9b1056.png)
E' un parametro di incerta valutazione, che dipende dalle condizioni atmosferiche, ma generalmente ha valori che possono essere trascurati per quanto riguarda il calcolo delle tensioni e delle correnti a regime, anche se le perdite possono essere importanti ai fini di una valutazione economica.
Per avere un'idea dell'ordine di grandezzza:
perdite sugli isolatori
le perdite su ogni isolatore sono dell'ordine di qualche watt  con tempo asciutto e fino ad un paio di decine con tempo umido. Si può nel complesso arrivare alla perdita di
con tempo asciutto e fino ad un paio di decine con tempo umido. Si può nel complesso arrivare alla perdita di 
perdite oer effetto corona
L'effetto corona si manifesta quando il campo elettrico sulla superficie del conduttore supera la rigidità dell'aria  in aria secca (quindi
in aria secca (quindi  efficaci).
efficaci).
Si manifesta con piccole scariche superficiali luminose e piccoli colpi secchi. Vengono emesse radiazioni elettromagnetiche che provocano radiointerferenze, sia dalle piccole scariche che dalle armoniche che si instaurano nella corrente della linea.
Esiste una tensione critica che dipende dalle condizioni atmosferiche e dal raggio del conduttore. Quest'ultimo deve essere superiore ad un determinato valore a seconda della tensione, per cui in AAT (380 kV) si adottano conduttori ingrossati con riempitivi inerti. Con i conduttori a fascio il raggio da prendere in considerazione è quello equivalente, abbastanza maggiore di quello dei singoli conduttori per cui anche tale soluzione è adottata in AAT.
Ad ogni modo, pur causando perdite, la conduttanza ha di solito un valore nettamente inferiore alla suscettanza e può anche essere trascurata nei calcoli.
Nel progettare le linee si fa in modo che la tensione critica sia inferiore alla tensione di fase.
cavi
La corrente assorbita a vuoto da un cavo ha una componente capacitiva, in quadratura con la tensione e ad essa proporzionale tramite la suscettanza b, ed una componente in fase che è responsabile della potenza attiva persa ed è proporzionale alla tensione tramite la conduttanza g. Il rapporto tra la componente in fase e quella in quadratura, uguale al rapporto tra conduttanza e suscettanza, è la tangente dell'angolo di perdita del dielettrico. Viene indicato con tanδ e permette di calcolare la conduttanza nota che sia la suscettanza
g = btanδ
Aumenta con l'aumentare della temperatura e vale
 : carta impregnata in olio, XLPE polietilene reticolato, EPR gomma etilenpropilenica, che sono i dielettrici usati nel cavi AT
: carta impregnata in olio, XLPE polietilene reticolato, EPR gomma etilenpropilenica, che sono i dielettrici usati nel cavi AT
- tanδ = 0,05: gomma e materiale termoplastico comune
Impedenza caratteristica (linea ideale)
Ideale significa considerare nulle r e g. Dalle espressioni precedenti per reattanza e suscettanza si ricava, per le linee aeree

Esercizi
Linea aerea
Linea a 

conduttore unico per fase: corda alluminio-acciaio 

deq = φ

![D = \sqrt[3]{{8 \times 8 \times 16}} = 10{,}1{\rm{m}}](/mediawiki/images/math/e/e/1/ee131efc026c9cc046c24810a8037745.png)

per un k = 1,03 ed una temperatura di funzionamento di  abbiamo
abbiamo
Ammettendo perdite sugli isolatori pari a  si ha
si ha
Linea in cavo
Cavo in olio fluido (cavo Emanueli: vedi riferimenti), isolamento in carta impregnata. Linea trifase con cavi disposti a trifoglio; 
Lo schermo è ondulato in senso longitudinale ed il suo spessore è di  . Assimilandolo ad una corona circolare di raggio interno
. Assimilandolo ad una corona circolare di raggio interno  , se ne può valutare la una resistenza kilometrica con la [1]
, se ne può valutare la una resistenza kilometrica con la [1]

Sempre con la [1], considerando un K=1,02 a 20°C abbiamo una
valore da considerare con schermi aperti, corretto sempre in base alla temperatura di funzionamento. Per la suscettanza, considerando una costante dielettrica relativa εr = 4 si ottiene, applicando la [3.a]
Per la reattanza, sempre considerando gli schermi aperti, si applica la [2.a] con
 e
e 
Con gli schermi cortocircuitati sia la r che la x sono modificate secondo, rispettivamente, le [2.c] e [2.d]. Occorre calcolare m che è il coefficiente di mutua induzione tra conduttore e rispettivo schermo che si calcola con la [2.a]

Quindi avremo per la reattanza un decremento pari a

e per la resistenza un incremento di
 che è il 57% della resistenza propria del coduttore, il che sta a significare che della stessa percentuale aumenteranno le perdite che ad esempio con una corrente di 400 A sono circa 25 kW per ogni km con schermi aperti (3rI2)
che è il 57% della resistenza propria del coduttore, il che sta a significare che della stessa percentuale aumenteranno le perdite che ad esempio con una corrente di 400 A sono circa 25 kW per ogni km con schermi aperti (3rI2)
quindi i nuovi valori sono
Assumendo infine pari tanδ = 0,003 si avrà una conduttanza
Alcuni dati tecnici
Corde nude
Alluminio-Acciaio
Ecco ad esempio le caratteristiche di una di esse

 : massa unitaria
: massa unitaria

 : resistenza a 20 °C
: resistenza a 20 °C
 : corrente massima (sovratemperatura di 30°C in aria stagnate a 40 °C)
: corrente massima (sovratemperatura di 30°C in aria stagnate a 40 °C)
Alluminio Rinforzato: ACCR 3M
Ampacity
Il costruttore indica anche il valore di corrente massima che a corda può ammettere in determinate condizioni. Nel caso specifico: 40°C di temperatura ambiente con vento di 0,6 m/s. E' denominata internazionalmente ampacity, una fusione di ampere e capacity.
Cavi AT
Isolante XLPE
Qui notiamo che come dato è fornita l'impedenza unitaria quindi il modulo di  sia per la disposizione a trifoglio che per quella in piano.
sia per la disposizione a trifoglio che per quella in piano.
in olio fluido
Riferimenti e bibliografia
- Sulle costanti fondamentali delle linee
- HIGH VOLTAGE XLPE CABLE SYSTEMS Technical User Guide - Brugg Cables
- NKT-cables
ELECTRIC MACHINERY and POWER SISTEM FUNDAMENTALS, Stephen J. Chapman, Mc Graw Hill, 2002
COMPLEMENTI DI IMPIANTI ELETTRICI- Lorenzo Fellin, DIADE, Padova 2005
TRASMISSIONE E DISTRIBUZIONE DELL'ENERGIA ELETTRICA VOL II, N. Faletti - P. Chizzolini, Patron Editore , Bologna 2005
Lezioni di TRASMISSIONE DELL'ENERGIA ELETTRICA -Antonio Paolucci, CLEUP EDITORE, Padova 1998

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)