Indice |
Premessa
Ho letto, qualche mese fa, "Perché E = mc2 ?" di
Brian Cox e Jeff Forshaw edito da Hoepli.
Mi è sembrata un'interessante, e direi anche appassionata, divulgazione sulla relatività. Poi magari nel momento cruciale lascia qualche perplessità ed insieme però anche desiderio di approfondire.
Ho allora scritto alcuni appunti per chiarirmi meglio i principali concetti. Già che c'ero, ho pensato di pubblicarli nel mio blog, non tanto per affermare "così stanno le cose", quanto piuttosto per stimolare all'approfondimento qualche fisico di maggior valore che dovesse per caso leggerli, sia precisandoli o anche correggendoli, sia proponendo qualche suo lavoro di maggior peso.
La formula fisica più famosa
È facile da ricordare e le sue conseguenze scientifiche, tecniche e sociali, sono state enormi.
Sto naturalmente parlando della formula proposta da Einstein centoquindici anni fa
dove m è la massa di un corpo e c la velocità della luce pari a  ,
,
E l'energia posseduta dal corpo.
- Me n'ero dimenticato, ma mi accorgo che su tale formula già avevo scritto qualcosa, come conclusione dell'articolo "Le forme dell'energia". Ponevo una domanda, sperando che qualcuno con conoscenze più approfondite delle mie chiarisse l'origine della formula. Ora sono proprio io che cerco di farlo: pensate un po'! ;-). Ad ogni modo...
Il fatto che la velocità della luce sia una costante della fisica, assioma assunto da Einstein come punto di partenza della teoria della relatività, fa sì che la formula stabilisca l'equivalenza tra massa ed energia, grandezze nate, e considerate fino a quel momento, separate.
Una qualsiasi variazione di energia corrisponde perciò ad una variazione di massa, e viceversa.
Assiomi di Einstein
- La velocità della luce è una costante fisica indipendente dal moto della sorgente o dell'osservatore
- Non esiste esperimento che possa identificare il moto assoluto.
Orologi
Un orologio è qualsiasi fenomeno fisico che si ripete con regolarità. Ogni ripetizione corrisponde ad un battito. Il numero di battiti è la misura di ciò che indichiamo come intervallo di tempo. Consideriamo un pendolo che oscilla: un battito è definito da una oscillazione completa. Possiamo immaginare di costruire un pendolo campione e chiamare "secondo", unità di misura del tempo, la durata della sua oscillazione completa. Una precisione maggiore nella misura della durata si ha con oggetti che oscillano più rapidamente. Ad esempio la tensione di rete compie 50 oscillazioni complete, mentre il pendolo campione ne fa una, quindi fornisce una definizione maggiore dell'intervallo di tempo. Un oscillatore al cesio compie
9.192.631.770 oscillazioni in un secondo, e costituisce l'orologio campione che definisce il secondo campione.
Possiamo immaginare anche un "orologio di luce" formato da due specchi che riflettono un raggio di luce: ogni volta che il raggio torna nello specchio da cui è partito, si ha un battito.
Il tempo non è uguale per tutti...
Supponiamo che un orologio di luce si trovi su un mezzo, in cui c'è l'osservatore A, che viaggia ad un velocità costante v rispetto ad un osservatore B.
Con riferimento alla figura:
per l'osservatore A un battito di orologio dura due volte il valore

(è detto tempo proprio di A: misurato da A per A);
per l'osservatore B invece dura due volte il valore
 (tempo misurato da B per A)
(tempo misurato da B per A)
dove, ritenendo applicabile il teorema di Pitagora,

cioè, isolando 


Le durate dello stesso battito sono dunque diverse per i due osservatori.
Indicando con γ il loro rapporto, si ottiene

Poiché il denominatore è un numero minore di uno,  , cioè per l'osservatore B la durata di un battito dell'orologio è maggiore di quella dell'osservatore A. Pertanto per l'osservatore B il tempo di A si dilata, dunque "scorre" più lentamente del tempo proprio, che B misurerebbe con un identico orologio fermo; A perciò invecchia più lentamente. A naturalmente non si accorge di alcun allungamento del suo tempo: per lui il tempo scorre sempre nello stesso modo, qualunque sia la velocità con cui sta muovendosi.
, cioè per l'osservatore B la durata di un battito dell'orologio è maggiore di quella dell'osservatore A. Pertanto per l'osservatore B il tempo di A si dilata, dunque "scorre" più lentamente del tempo proprio, che B misurerebbe con un identico orologio fermo; A perciò invecchia più lentamente. A naturalmente non si accorge di alcun allungamento del suo tempo: per lui il tempo scorre sempre nello stesso modo, qualunque sia la velocità con cui sta muovendosi.
Si potrebbe osservare che il risultato può dipendere dal tipo di orologio. Ma, se così fosse, un pendolo ed un orologio di luce perfettamente sincronizzati, uscirebbero dal sincronismo sul mezzo in moto. Ciò permetterebbe all'osservatore
A di riconoscere il moto del suo mezzo, cosa che va contro il secondo postulato di Einstein: si può solo riconoscere un moto relativo, cioè una velocità rispetto a qualcos'altro, ma non un proprio moto assoluto.
Naturalmente la scienza esige che una deduzione teorica sia verificata con l'esperimento.
Alle velocità "terrestri", nettamente inferiori alla velocità della luce, la verifica non è facile in quanto la differenza è impercettibile.

Su un treno che viaggia a trecento chilometri all'ora, il rallentamento è dunque pari a poco più di  per ogni anno.
per ogni anno.
Il muone è una particella elementare identica all'elettrone, se non fosse per la sua massa circa duecento volte maggiore. La sua durata di vita, a riposo, che è il suo tempo proprio, vale  . Verso la fine degli anni novanta gli scienziati del Brookhaven National Laboratory di New York, portarono un fascio di muoni, nel sincrotrone a gradienti alternati, ad una velocità pari al 99,94% della velocità della luce. A tale velocità
. Verso la fine degli anni novanta gli scienziati del Brookhaven National Laboratory di New York, portarono un fascio di muoni, nel sincrotrone a gradienti alternati, ad una velocità pari al 99,94% della velocità della luce. A tale velocità

nel tempo ad essi a disposizione, cioè 2,2 microsecondi, avrebbero dovuto percorrere

cioè, essendo di  il diametro del sincrotrone, un numero di giri pari a circa 15
il diametro del sincrotrone, un numero di giri pari a circa 15

In realtà invece ne percorrevano oltre 400, il che significava che la loro durata a quella velocità era molto maggiore di quella a riposo, pari ad oltre 60 microsecondi. Teoricamente avrebbe infatti dovuto diventare

L'esperimento dunque conferma la teoria di Einstein.
...e nemmeno lo spazio
La conclusione del precedente paragrafo, mostra che la vita del muone si è allungata. Questo è quanto deducono gli sperimentatori, per i quali il muone si muove ad una velocità prossima a quella della luce. Ma per un osservatore solidale con il muone, il muone è fermo, quindi la sua durata deve essere di 2,2 microsecondi. Però, come gli sperimentatori esterni, deve contare oltre quattrocento giri (432 per la precisione). Per l'osservatore solidale con il muone, la distanza percorsa è pari ad s, quindi  , quindi ogni giro è lungo
, quindi ogni giro è lungo
 per cui il diametro del sincrotrone risulta
per cui il diametro del sincrotrone risulta  cioè si è ridotto nella stessa proporzione di cui si è allungato il tempo per l'osservatore esterno.
cioè si è ridotto nella stessa proporzione di cui si è allungato il tempo per l'osservatore esterno.
Naturalmente tutto è relativo
Se l'osservatore A fa lo stesso esperimento dell'osservatore B, troverà che l'orologio di B, identico al suo, rallenta.
L'osservatore B infatti, si muove alla stessa velocità v rispetto ad A. Entrambi possono sostenere di essere fermi e che è l'altro a muoversi
Quindi per A sarà  con
con  durata misurata da B sul suo orologio ( tempo proprio di B) e
durata misurata da B sul suo orologio ( tempo proprio di B) e  durata misurata da A.
durata misurata da A.
Sarà allora  come
come  .
.
Il paradosso dei gemelli
Ma se per entrambi l'orologio dell'altro rallenta rispetto al suo, dopo un viaggio di andata e ritorno di uno dei due, cosa segneranno i rispettivi orologi al ritorno, se per tutta la durata del viaggio ognuno dei due camminava più lentamente dell'altro?
La situazione è nota come paradosso dei gemelli.
Osserviamo a questo punto che le considerazioni precedenti riguardavano sistemi in moto relativo a velocità costante, cioè sistemi inerziali. Per effettuare un viaggio di andata e ritorno, occorre accelerare per raggiungere la velocità costante di crociera, quindi decelerare, per poter invertire la direzione del moto, quindi accelerare di nuovo per raggiungere la velocità di crociera e decelerare nuovamente per arrivare. Nelle fasi di accelerazione e decelerazione, i sistemi non sono più inerziali ed occorre tenere conto dell'accelerazione.
Lo farà la teoria della relatività generale, che non trattiamo, accennando solo al fatto che nei sistemi accelerati il tempo rallenta tanto più quanto maggiore è l'accelerazione.
Lo spaziotempo (cronotopo)
Esiste dunque solo il moto relativo e nessuno può dire chi è fermo e chi si muove. La costanza della velocità della luce, indipendente dal moto della sorgente, implica, come visto, che spazio e tempo siano diversi per gli osservatori in moto relativo. Distanze nello spazio ed intervalli di tempo, sono entrambi soggettivi.
Non esistono punti dello spazio ed istanti assoluti, validi per ogni osservatore dell'universo.
Eventi
Ogni fenomeno fisico è, per ogni osservatore, un evento.
Un evento è definito da quattro parametri: tre coordinate spaziali ed una temporale.
Per osservatori in moto relativo, le quattro coordinate dello stesso evento sono in generale diverse, come mostrato in precedenza: dilatazione dei tempi e contrazione degli spazi.
Solo l'evento, che coinvolge contemporaneamente tutte e quattro le coordinate, è unico per tutti gli osservatori.
Tutti gli osservatori devono allora concordare sugli eventi in sé, nonché sulla distanza che li separa nello spaziotempo e sull'ordine in cui si succedono. Quest'ultima è l'esigenza della causalità: l'effetto deve, per tutti, essere conseguente alla causa.
Se qualcuno al mattino si sveglia, esce dalla camera da letto, si lava in bagno, si veste ed in cucina fa colazione, per tutti deve essere così: non è ammesso che, per qualcun altro, faccia, ad esempio, colazione prima di svegliarsi.
Rappresentazione grafica dello spazio-tempo
Un intervallo temporale può essere trasformato in una distanza spaziale moltiplicando l'intervallo per una velocità. E' quello che, ad esempio, si fa per misurare le enormi distanze astronomiche. Si usano, come noto, gli anni-luce. Un anno-luce è la distanza percorsa dalla luce in un anno. Un anno-luce corrisponde ad una distanza di

un numero impronunciabile di metri senza ricorrere ai multipli con i quali si può dire oltre  .
.
Per semplicità consideriamo una sola variabile spaziale, x, ed il tempo, t, lo moltiplichiamo per la velocità della luce, c, costante positiva.
Consideriamo un piano cartesiano dove in ascissa riportiamo x ed in ordinata, ct.
Il piano rappresenta una sezione dello spaziotempo in cui le coordinate y e z sono costanti.
Lo spaziotempo è lo stesso per tutti gli osservatori: è il nuovo riferimento "assoluto".
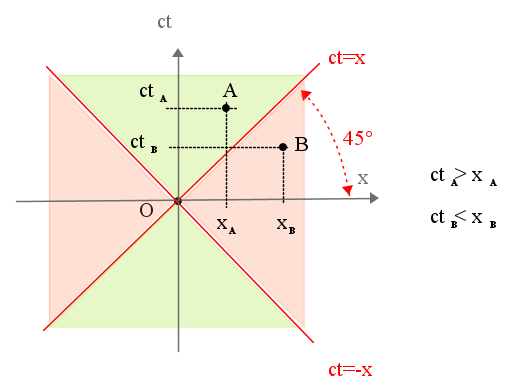
Ogni osservatore posizionerà l'evento iniziale, cioè, per l'esempio riportato, il "qualcuno che si sveglia", nell'origine del piano cartesiano, O, e, per l'evento finale, A, cioè il "qualcuno che fa colazione", misurerà una distanza spaziale xA ed una distanza temporale ctA, dall'evento iniziale; per ognuno degli osservatori in moto relativo, tali coordinate saranno diverse, quindi l'evento A corrisponderà ad un diverso punto del piano cartesiano.
La parte superiore del piano, dove t > 0 ( è c > 0), rappresenta, teoricamente, il futuro per l'evento O; quella inferiore, dove t < 0, il passato.
Però non tutti i punti dei semipiani possono rappresentare eventi legati da un rapporto causa-effetto con l'evento posto nell'origine, che è l'evento iniziale per i punti del semipiano superiore, finale per i punti di quello inferiore. Cioè non tutti i punti del semipiano superiore possono rappresentare il futuro di O né quelli del semipiano inferiore il suo passato.
Le bisettrici tracciate in rosso, di equazione ct = x e ct = − x rappresentano punti, cioè eventi, per i quali la distanza spaziale rispetto all'evento iniziale è raggiunta con una velocità pari a c.
Esse dividono il piano in quattro zone.
Per gli eventi posizionati all'interno delle zone verdi, come A ad esempio, la distanza spaziale è raggiunta con una velocità inferiore a c; infatti:
 .
.
Invece, per gli eventi situati all'interno delle due zone rosse, come ad esempio B, la distanza spaziale richiede una velocità maggiore di c:
 .
.
Poiché la velocità della luce non può essere superata, solo i punti appartenenti alle zone verdi possono rappresentare eventi che dipendono da O, cioè del futuro o del passato di O, che soddisfano al principio di causalità.
Le zone verdi sono chiamate "Cono di luce".
La distanza spazio-temporale tra gli eventi
Distanze spaziali e temporali sono dunque soggettive, considerate separatamente.
Non lo deve però essere la distanza nello spaziotempo: su quella tutti gli osservatori devono concordare; non solo, ma imponiamo anche che devono concordare sul succedersi degli eventi, cioè imponiamo il principio di causalità: la causa deve, per tutti, precedere l'effetto.
Per la distanza tra O ed A nello spazio-tempo, dobbiamo allora trovare un'espressione matematica che fornisca lo stesso risultato per tutti gli osservatori.
Una possibile, potrebbe essere la pitagorica

valida nello spazio cui siamo abituati, che definiamo euclideo.
Essa però rappresenta una circonferenza di raggio s e centro O. Quindi contiene eventi interni al cono di luce come A ma anche esterni come B.
La formula pitagorica, o distanza euclidea, non può essere perciò accettata.
Il luogo degli eventi A, che rappresentano il futuro di O, che trova concordi tutti gli osservatori sulla distanza spazio-temporale da O, deve trovarsi nel semipiano superiore, nella zona verde, affinché sia salvaguardato il principio di causalità
L'espressione che soddisfa questa proprietà è

Essa rappresenta un'iperbole i cui asintoti sono le bisettrici considerate in precedenza.
Nota:
- quanto detto vale anche per l'espressione in cui si usano le differenze tra le coordinate spaziali e temporali di due eventi. Quindi

Consideriamo due sistemi, A e B, in moto relativo con velocità v costante. Su ogni sistema fissiamo un sistema di riferimento con asse x orientato in modo concorde con la velocità.
Dal punto di vista di A, dopo un certo tempo, tA da lui misurato con il suo orologio, il suo spostamento secondo il suo asse x sarà nullo: xA = 0. Dal punto di vista di B invece, lo spostamento di A secondo il suo asse x, sarà xB dopo il tempo tB misurato dal suo orologio con xB = vtB.
La distanza spazio-temporale calcolata da A sarà  uguale a quella calcolata da B
uguale a quella calcolata da B  per cui
per cui
 da cui si ricava
da cui si ricava

Il tempo in A si dilata nello stesso modo che si era già visto.
La considerazione dello spaziotempo come un assoluto per tutti gli osservatori e del modo di calcolare la distanza tra gli eventi che trova concordi tutti gli osservatori, porta alle conseguenze già trovate per altra strada.
Velocità nello spaziotempo
Nessuno può scoprire di essere in moto rispetto a qualcosa cui attribuire la quiete assoluta, cioè uno spazio assoluto che è come un palcoscenico in cui si muovono le cose, ma si può solo constatare un moto relativo del proprio sistema di riferimento rispetto ad altri sistemi.
Tutti invece possono constatare il loro movimento nello spaziotempo, non solo, ma anche determinarne la velocità. Tutti troveranno lo stesso risultato, che è la velocità della luce c.
In ogni sistema di riferimento inerziale ogni orologio, fermo in esso, segna un tempo t che corrisponde alla distanza spaziotemporale pari ad s = ct, poiché, per quell'orologio, è nullo lo spostamento (x = 0). Su tale distanza, ogni altro osservatore concorda. Per ogni secondo che passa, l'orologio percorre, nello spaziotempo, una distanza pari a c, cioè si sposta nello spaziotempo alla velocità della luce.
Il moto nello spazio tridimensionale è allora l'ombra del moto universale nello spaziotempo. che avviene, per ogni cosa, alla velocità della luce.
La velocità universale di ogni cosa nello spaziotempo, si suddivide, per un corpo in moto a velocità costante in un sistema inerziale, parte nello spazio e parte nel tempo, che è un modo per dire che, per esso, la velocità con cui si sposta nel tempo è inferiore rispetto a quella di chi è a riposo nello stesso sistema: cioè ritroviamo che il tempo rallenta per chi è in moto in quel sistema di riferimento rispetto a chi è fermo. Non esiste, d'altra parte, nessun sistema di riferimento privilegiato e tutti, nel sistema di riferimento ad essi solidale, arrivano alle stesse conclusioni sul tempo degli altri rispetto al loro tempo, cioè il tempo proprio.
Viaggiatori nello spaziotempo
La matematica descrive algebricamente lo spazio quadridimensionale senza grossi problemi e potremmo accontentarci della sua potenza astratta. Però il nostro legame con lo spazio tridimensionale, quasi ci impone di cercare una rappresentazione geometrica dei concetti legati allo spazio-tempo.
Il viaggiatore nello spaziotempo procede a velocità costante pari a c, ed è libero di scegliere una qualsiasi direzione all'interno del cono di luce di cui lui stesso è il vertice.
Può "spendere" tutta la velocità c nel tempo, viaggiando parallelo e concorde all'asse temporale, il cui verso indica il futuro, il che succede quando è fermo nel suo sistema di riferimento spaziale. L'asse temporale rappresenta infatti la dimensione spaziale lungo la quale non può stare fermo: le coordinate spaziali possono rimanere immutate, ma non quella temporale.
Può deviare verso destra o verso sinistra entro un angolo massimo di 45° rispetto all'asse del tempo. In tale caso, una parte della velocità è spesa nello spazio, l'altra nel tempo. Quest'ultima, quindi, diminuisce rispetto a quando il viaggiatore procedeva verso il futuro parallelamente all'asse del tempo, il che equivale a dire che il suo tempo scorre più lentamente. Se procede nella direzione che forma 45° con l'asse del tempo, significa che sta viaggiando nello spazio alla velocità della luce e per lui, in tal caso, il tempo si ferma.
La traiettoria seguita da un viaggiatore nello spazio-tempo è la linea di universo.
Quantità di moto nello spaziotempo
Consideriamo una successione di eventi, all'interno del cono di luce. Indichiamo con A l'evento iniziale e con B l'evento finale. Immaginiamo che si tratti dello spostamento di un corpo di massa a riposo (cioè ferma nel sistema di riferimento ) m0 che, per un osservatore inerziale, avviene alla velocità v secondo la direzione dell'asse x
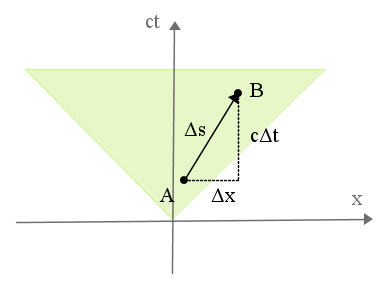
Il segmento che unisce i punti A e B nel diagramma spazio-tempo con una sola coordinata spaziale x, rappresenta la distanza spaziotemporale tra i due eventi, che sono, rispettivamente la partenza (evento iniziale) e l'arrivo (evento finale) del corpo in movimento.
Indichiamo il segmento con Δs ed orientiamolo verso l'evento finale. Il segmento orientato così ottenuto, rappresenta direzione e verso dello spostamento del corpo nello spaziotempo.
Le componente spazio di tale vettore è Δx, la componente tempo cΔt.
Per ogni corpo, la velocità di spostamento nello spaziotempo è la velocità della luce, come visto in precedenza.
Il rapporto  è una grandezza, omogenea con il tempo, su cui gli osservatori di qualsiasi sistema inerziale sono d'accordo.
è una grandezza, omogenea con il tempo, su cui gli osservatori di qualsiasi sistema inerziale sono d'accordo.
Ricordando che

si ha

dividiamo per tale rapporto tutte le componenti e moltiplichiamo per m0.



Possiamo assumere il segmento orientato che unisce A e B, come quantità di moto del corpo di massa m0 in moto nello spaziotempo, poiché è costante, uguale per tutti gli osservatori inerziali.
Tale vettore, noto come quadrimpulso (ricordiamo che le coordinate spaziali sono tre) spaziotemporale ha quattro componenti: tre nello spazio ed una nel tempo, tutte dipendenti dalla massa a riposo proporzionalmente a γ che, sviluppata in serie è:

Componente spaziale
Ponendom = γm0
grandezza che Einstein stesso chiamò massa relativistica, la componente spaziale può essere espressa con
p = mv
Sostituendo a γ il suo sviluppo in serie, possiamo immediatamente osservare che, per velocità molto inferiori a quella della luce  espressione che coincide con la quantità di moto della meccanica classica.
espressione che coincide con la quantità di moto della meccanica classica.
L'espressione non approssimata rappresenta allora l'espressione più completa della quantità di moto nello spazio.
Componente temporale
Moltiplicando per c la componente temporale, otteniamo una grandezza che ha le dimensioni dell'energia, per cui potremo scrivere
E = mc2
Possiamo interpretare tale espressione come energia totale del corpo nello spaziotempo.
Sostituendo a γ il suo sviluppo in serie abbiamo

Il secondo termine del secondo membro è proprio l'espressione nota dell'energia cinetica del corpo di massa m0 alla velocità v nella meccanica classica. Gli altri termini contengono tutti la velocità spaziale, quindi sono contributi che vanno affinano il calcolo dell'energia cinetica rispetto alla meccanica classica.
Il primo termine è invece una costante indipendente dalla velocità spaziale v.
La indicheremo con E0, e possiamo interpretarla come l'energia attribuibile al corpo di massa m0, quando esso è fermo nel sistema di riferimento.
È un'energia dipendente unicamente dalla massa del corpo e, poiché la velocità della luce è una costante, è identificabile praticamente con la massa stessa.
Si tratta di un risultato sorprendente:
un corpo a riposo nel sistema di riferimento,  , possiede una energia
, possiede una energia
E0 = m0c2
L'energia cinetica del corpo, cioè l'energia che esso acquista in virtù della sua velocità v, è data da

Tale espressione dell'energia cinetica coincide, come già detto, con quella della meccanica classica per velocità molto inferiori a quella della luce:

Ma soffermiamoci sull'espressione dell'energia del corpo a riposo.
Un corpo dotato di massa è energia allo stato potenziale. L'esistenza della massa è un modo di manifestarsi dell'energia; possiamo anzi dire che ne è la manifestazione fondamentale e che ogni variazione di energia interna del corpo si associa ad una variazione della sua massa a riposo.
Il modo in cui ci si è arrivati è teorico, conseguenza di elaborazioni matematiche che hanno condotto a nuove considerazioni sulla realtà fisica. La matematica è uno strumento di indagine della realtà fisica la cui potenza sorprende ed affascina sempre, Ma è poi sempre indispensabile verificare con l'esperimento i suoi risultati.
La possibilità di trasformare la massa in energia e viceversa, doveva dunque essere verificata dopo che Einstein l'aveva scritta nel 1905.
Le reazioni nucleari, come noto, hanno confermato tale trasformazione.
Nella fissione nucleare, ad esempio, un atomo di Uranio 235 colpito da un neutrone, si spezza in un atomo di Bario ed uno di Kripton liberando tre neutroni. La massa delle particelle generate dalla fissione è inferiore a quella dell'atomo di Uranio. La differenza si manifesta sotto forma di vari altri tipi di energia: elettromagnetica, termica, cinetica. La quantità di energia prodotta è enorme.
Nella fusione nucleare invece, l'unione di un atomo di deuterio con un atomo di trizio, produce un atomo di Elio ed un neutrone che, complessivamente, hanno una massa inferiore a quella degli atomi di partenza: la differenza di massa è l'energia che si ottiene.
Se indichiamo con ΔE la variazione dell'energia interna di un corpo, di qualunque natura essa sia, la massa del corpo varia della quantità

Il processo di conversione energia-massa è presente in ogni fenomeno fisico.
Anche se la differenza è impercettibile, una molla caricata ha una massa maggiore di una molla scaricata; una tazza di tè caldo ha una massa maggiore della stessa tazza di tè freddo; la massa di un legno prima di bruciare è maggiore della massa di tutti i prodotti della combustione: la differenza corrisponde all'energia irradiata, termica ed elettromagnetica. Se un fuoco di legna che brucia genera un kW per otto ore, l'energia totale irradiata è

il che corrisponde ad una diminuzione di massa della legna pari a

cioè un terzo di microgrammo!
Piccola conclusione
La formula più famosa del mondo ha dunque insegnato che la massa è l'energia e che basterebbe una piccola quantità di massa per ottenere l'energia che vogliamo.
Con quindici microgrammi al secondo, quindi poco più di un grammo al giorno, si produrrebbe una potenza di  in grado di soddisfare il fabbisogno di energia elettrica di una città come Milano.
in grado di soddisfare il fabbisogno di energia elettrica di una città come Milano.
Ma distruggere la massa oltre che complicato, è anche inefficiente.
Nelle centrali a fissione, ad esempio, solo una piccola quantità di combustibile è disintegrato, il resto è trasformato in elementi più leggeri che generano scorie radioattive pericolosissime.
Ne deve essere fatta ancora molta di strada per arrivare a sfruttare al meglio l'enorme energia potenziale racchiusa nella massa.
La fusione nucleare controllata, che non produce residui pericolosi, è l'obiettivo che si cerca di raggiungere.
Nel frattempo complicazione ed inefficienza non sono stati freni sufficienti ad impedire la proliferazione di armi atomiche.
Dovevamo pur avere pronta la possibilità di autodistruggerci, senza aspettare i tempi della natura!
È una constatazione amara ma la formula più famosa del mondo non è responsabile di tale situazione.
L'unica possibilità, come individui, è sperare o sognare che l'uomo usi la conoscenza delle leggi fisiche, per alimentare serenità e bellezza e vivere in armonia con la natura di cui è solo una piccola e non indispensabile parte.
Altri riferimenti
Einstein illustra la formula nel suo libro divulgativo Relatività
Cap 1 - Paragrafo 15
[..]
Secondo la teoria della relatività, l'energia cinetica di un punto materiale di massa m [NB: è la massa a riposo, che io ho indicato con m0], non viene più data dalla nota espressione  ma da quest'altra γmc2.
ma da quest'altra γmc2.
Tale espressione tende all'infinito quando la velocità si avvicina alla velocità c della luce.[..]
Il suo sviluppo in serie è dato da
 .
.
Per  piccolo in confronto all'unità, il terzo termine è sempre piccolo rispetto al secondo, che è il solo considerato nella meccanica classica. [..]
piccolo in confronto all'unità, il terzo termine è sempre piccolo rispetto al secondo, che è il solo considerato nella meccanica classica. [..]
Il termine mc2 non è altro che l'energia posseduta dal corpo.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)