Indice |
Premessa
Questa è la revisione leggermente ampliata di un vecchio articolo: le idee nuove scarseggiano...
Ad ogni modo, stavolta, la riedizione si è anche resa necessaria per un errore grossolano sul valore di una corrente nel vecchio articolo. Devo ringraziare il lettore che lo ha evidenziato in questo thread, purtroppo credendo di essere lui in errore: si sbagliava, ahimé! Spero, se pur in ritardo, di rimediare alla figuraccia protrattasi negli anni, anche se l'amarezza per non essermene mai accorto rimarrà.
Il vecchio articolo era la risposta ad un quesito pervenuto nel forum:
Quando un sistema trifase ha solo tre fili, per esempio perché il trasformatore ha il secondario a triangolo, è possibile costruire un neutro artificiale?
In teoria sembrerebbero bastare tre impedenze a stella usandone il centro per derivare il neutro artificiale. L'articolo mostra il perché non si possono utilizzare resistenze o reattanze semplici ed illustra una struttura magnetica adatta allo scopo, spesso usata in media tensione e tornata di attualità anche in bassa tensione, non solo per ottenere un neutro artificiale ma anche come compensatore di armoniche: il reattore trifase a zig-zag.
Il neutro artificiale
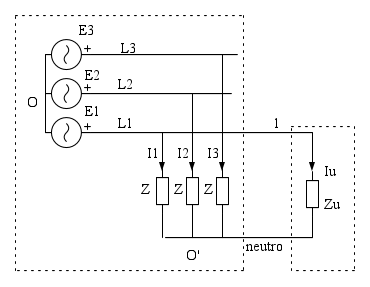
Un'impedenza Zu deve essere alimentata alla tensione  dove U è la
concatenata del sistema trifase. Realizzata una stella di impedenze Z il carico monofase potrebbe essere alimentato tra il centro stella ed una fase qualsiasi.
dove U è la
concatenata del sistema trifase. Realizzata una stella di impedenze Z il carico monofase potrebbe essere alimentato tra il centro stella ed una fase qualsiasi.
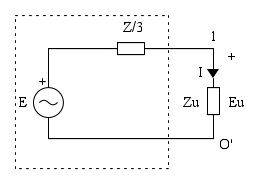
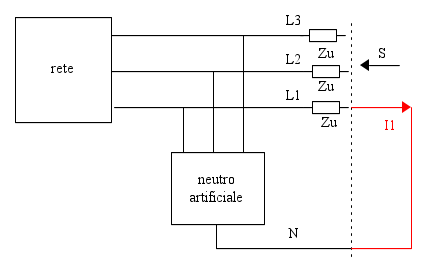
 , se, per semplicità consideriamo nulle le impedenze della linea, come nello schema sopra. Il circuito su cui ragionare è il seguente
, se, per semplicità consideriamo nulle le impedenze della linea, come nello schema sopra. Il circuito su cui ragionare è il seguente
La tensione ai capi del carico sarà:
 .
.
Quindi

Cioè

Se ad esempio  e
e  sono pure resistenze, E ed Eu sono in fase e la relazione precedente nell'ipotesi di desiderare
sono pure resistenze, E ed Eu sono in fase e la relazione precedente nell'ipotesi di desiderare  con
con  fornisce
fornisce

Supponiamo si tratti di un carico resistivo che a  assorbe
assorbe  . Si ha
. Si ha ed
ed  il che significa che la stella di resistenze, se permanentemente inserita assorbirebbe, senza carico monofase collegato,
il che significa che la stella di resistenze, se permanentemente inserita assorbirebbe, senza carico monofase collegato,  dissipando
dissipando  ben più dei
ben più dei  del carico.
del carico.
Non cambia molto con il carico collegato.
Ad esempio nella resistenza R della linea L1 che risulta in parallelo al carico, c'è una corrente  . Non molto diverse le altre due correnti.
. Non molto diverse le altre due correnti.
Per esercizio ad ogni modo calcoliamole tutte

Agli stessi risultati possiamo pervenire anche applicando Millman alla stella squilibrata che il parallelo di R_u con R determina


Con reattanze induttive non ci sarebbe dispersione di potenza ovviamente, ma risulta un eccessivo impegno di potenza reattiva sia a vuoto che a carico. Desiderando ottenere sempre 220 V su una resistenza da 22 ohm, la reattanza di ogni ramo della stella deve avere il valore che si ricava dall'espessione in precedenza usata. Basta sostituire jX ad R quindi, con alcuni passaggi, ricavare X

La potenza reattiva impegnata a vuoto è

Con il circuito di Thevenin calcoliamo la corrente sul carico

Quindi risaliamo alle correnti sulle reattanze

La potenza reattiva impegnata a carico è

quasi il quadruplo della potenza attiva sulla resistenza il che significa un fattore di potenza pari a 0,25.
Se poi controlliamo le tensioni stellate otteniano una discreta dissimmetria

In conclusione la strada di tre impedenze a stella per costruire un neutro artificiale non è una strada praticabile.
I problemi esposti diventano trascurabili solo se il carico monofase assorbe una piccola potenza, come nel caso di strumenti di misura.
Osservazioni
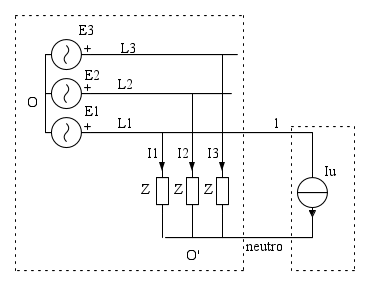
Possiamo vedere le cose immaginando di sostituire all'impedenza tra fase e neutro artificiale un generatore ideale di corrente che eroga la stessa corrente assorbita dall'impedenza:
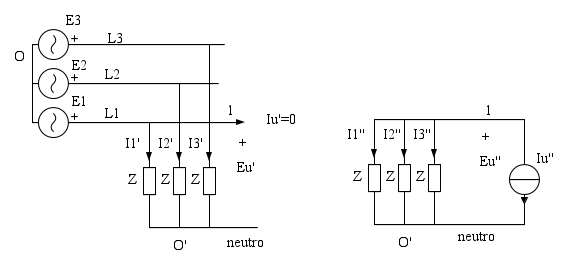
Ora applichiamo la sovrapposizione degli effetti facendo agire in un primo circuito tutti i generatori di tensione e spegnendo, quindi aprendo, il generatore di corrente, ed in un secondo circuito il solo generatore di corrente spegnendo, quindi cortocircuitandoli, i generatori di tensione
Dal primo circuito si ha


Dal secondo


quindi abbiamo


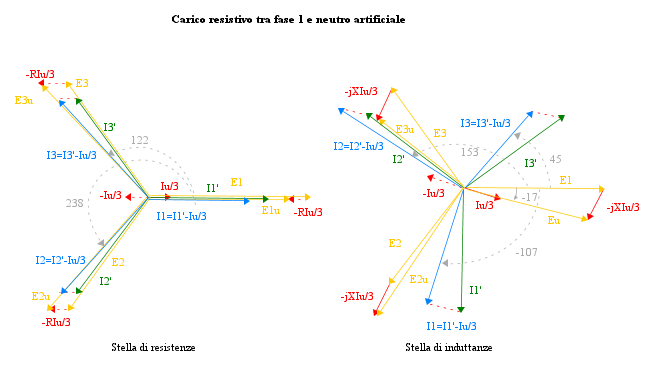
Le espressioni ricavate mostrano che, a carico, la corrente sulle impedenze è la composizione delle correnti a vuoto (cioè senza carico derivato tra una fase ed il loro centro stella) con un terzo della corrente sul carico tra fase e neutro.
La tensione sul carico è le tensione stellata cui si sovrappone la caduta su una delle impedenze della stella dovuta ad un terzo della corrente di carico: tale tensione è detta omopolare in quando dovuta a correnti che hanno la stessa fase nelle tre fasi.
E' perciò indispensabile che le correnti a vuoto siano il più piccole possibile, mentre occorre che le correnti del carico non alterino eccessivamente le tensioni.
Ciò si ottiene con un componente che presenta rispetto alle tensioni di fase un'impedenza elevata ed un'impedenza bassa rispetto alle correnti omopolari.
I seguenti grafici illustrano i casi numerici in precedenza esaminati
Reattori a zig-zag
Per avere dunque un neutro artificiale permanente per carichi di potenza, occorre, come detto, una stella trifase che presenti un'impedenza elevata rispetto alle tensioni simmetriche, ma che, rispetto ad un carico collegato tra il suo centro ed una fase, presenti una impedenza molto bassa.
Il reattore trifase a zig-zag ha proprio questa caratteristica.

Su un nucleo magnetico a tre colonne sono disposti 6 avvolgimenti. Il primo avvolgimento di ogni colonna è collegato in serie al
secondo avvolgimento della colonna successiva. Le tre serie sono collegate a stella.
Il reattore è inserito in rete come nella seguente figura

Quando non c'è il carico monofase ogni mezzo avvolgimento di colonna è percorso da correnti di ugual modulo ma sfasate di  . La forza magnetomotrice è dunque diversa da zero ed il flusso magnetico che si instaura nella colonna dà luogo ad una elevata reattanza che è dello stesso ordine di grandezza di quella di un trasformatore a vuoto; la indicheremo con
. La forza magnetomotrice è dunque diversa da zero ed il flusso magnetico che si instaura nella colonna dà luogo ad una elevata reattanza che è dello stesso ordine di grandezza di quella di un trasformatore a vuoto; la indicheremo con  . Le correnti nei due semiavvolgimenti sono perciò piccole, corrispondenti alle normali correnti a vuoto di un trasformatore.
. Le correnti nei due semiavvolgimenti sono perciò piccole, corrispondenti alle normali correnti a vuoto di un trasformatore.
La corrente di un carico monofase si suddivide, come visto in precedenza, in tre parti.
Ogni semiavvolgimento di una stessa colonna è percorso da correnti uguali in modulo e fase, che circolano però in senso inverso. La forza magnetomotrice complessiva è dunque nulla e, con essa, il flusso magnetico della colonna. La reattanza corrispondente ad ogni fase è allora solo quella del flusso di dispersione tra i due semiavvolgimenti, quindi è molto bassa, di valore percentualmente comparabile a quella di cortocircuito di un trasformatore. La indicheremo con 
Rn è la resistenza di messa a terra del neutro adottata in genere in media tensione come precisato più avanti ( paragrafo "Quando e come").
Reti di sequenza
Generalmente questo tipo di problemi è analizzato ricorrendo alle reti di sequenza.
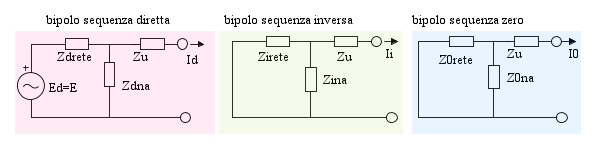
Ogni situazione squilibrata, e l'alimentazione monofase è la più squilibrata di tutte, può essere ricondotta alla
considerazione dei tre bipoli di sequenza, diretta, inversa e zero (od omopolare) determinati nella sezione di impianto che interessa, nel nostro caso quella tratteggiata ed indicata con S nella figura che segue
In tale rete il collegamento franco di un estremo libero di una delle impedenze Zu con il neutro artificiale N corrisponde alla derivazione di un carico monofase nella rete di partenza. Nello schema precedente il collegamento con resistenza nulla è in rosso.
Le altre due impedenze Zu con un estremo non collegato servono per mantenere la simmetria della rete nella sezione S.
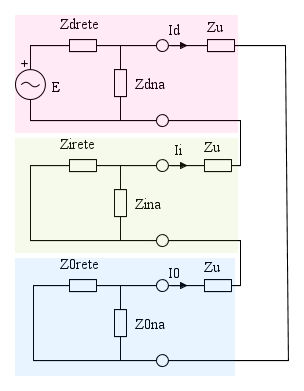
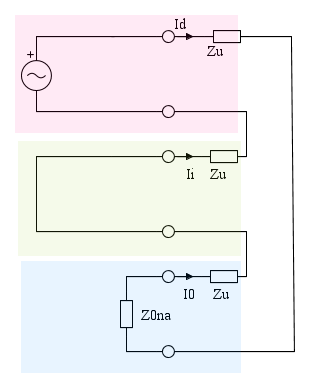
I tre bipoli sono allora rappresentati nella seguente figura. Le tensioni di rete siano simmetriche, quindi esista solo la terna di tensioni di sequenza diretta di valore Ed = E
La corrente nel carico monofase è la corrente nel collegamento di cortocircuito effettuato che corrisponde alla serie dei tre bipoli di sequenza.
Con le tre impedenze semplici a stella si ha:

Le impedenze di sequenza sono cioè tutte identiche all'impedenza di un ramo della stella.
Con il reattore a zig-zag:

le impedenze di sequenza diretta ed inversa sono molto elevate, dell'ordine dell'impedenza a vuoto di un trasformatore Yzn con identici avvolgimenti secondari, mentre  è molto bassa dell'ordine, ma anche inferiore, dell'impedenza di cortocircuito del trasformatore.
è molto bassa dell'ordine, ma anche inferiore, dell'impedenza di cortocircuito del trasformatore.
- Nota: generalmente la parte resistiva dell'impedenza del reattore si può trascurare quindi porre
Per la rete ipotizziamo che le impedenze di sequenza diretta ed inversa siano molto basse, molto inferiori comunque sia  che a
che a 
Poniamo perciò

e, poiché il neutro non è accessibile, si ha

Il calcolo della corrente  può allora essere svolto sul circuito seguente
può allora essere svolto sul circuito seguente

Con le tre impedenze a stella è  .
.
Ritroviamo lo stesso risultato determinato con Thevenin.
Con il reattore a zig-zag  .
.
Tale impedenza, come detto, è molto bassa rispetto a  .
.
Quando il carico monofase è scollegato, il carico per la rete corrisponde al solo reattore a zig-zag la cui impedenza di sequenza diretta è molto elevata, come quella di un trasformatore a vuoto.
Quando e come
Il reattore a zig-zag per il neutro artificiale, è usato in Media Tensione.
Spesso il trasformatore AT/MT è uno stella-triangolo. In tal modo gli avvolgimenti di alta tensione possono essere dimensionati per una tensione di isolamento che è il 58% della tensione nominale (cioè per la tensione stellata invece che per la concatenata) con un notevole risparmio sul costo.
Negli impianti industriali per evitare sovratensioni ed interrompere immediatamente il circuito in caso di guasto, conviene avere, anche in media tensione, oltre che in bassa, il neutro collegato a terra. Da qui la necessità di creare nei circuiti MT il neutro artificiale. Neutro che poi è collegato all'impianto di terra mediante una resistenza per limitare la
corrente di guasto fase-terra.
La resistenza è scelta in modo da avere una corrente di guasto di circa 100 A affinché possa essere facilmente rivelata da riduttori di corrente toroidali e sia abbastanza superiore alle correnti capacitive d'esercizio così da evitare interventi intempestivi delle protezioni.
In bassa tensione l'esigenza di un neutro artificiale in genere non esiste in quanto il neutro è distribuito ed è già collegato a terra: i trasformatori di distribuzione sono in genere DYn.
Potrebbero comunque verificarsi situazioni particolari per prevederne l'uso.
Compensatori armonici
E' da segnalare un'importante applicazione in bassa tensione dei reattori a zig-zag, cresciuta di importanza con la diffusione dei carichi non lineari che assorbono correnti di forma non sinusoidale con un alto contenuto armonico. Tali carichi (raddrizzatori, inverter ecc.) possono essere considerati come generatori di correnti armoniche che provocano cadute sulle impedenze di rete, deformandone la tensione. Il fenomeno è tanto più sensibile quanto più la potenza del carico distorcente si avvicina a quella del trasformatore e può diventare assolutamente intollerabile quando il generatore non è la rete pubblica ma un gruppo elettrogeno.
Occorre allora fare in modo che le impedenze "trovate" da queste correnti siano il più piccole possibili. Le correnti di terza armonica, cioè di frequenza tripla della fondamentale, ed i suoi multipli costituiscono in un sistema trifase, terne omopolari e l'impedenza interessata è quella alla sequenza zero. I reattori a zig-zag hanno, come detto, impedenze di sequenza zero che possono essere molto basse per cui impediscono o quantomeno attenuano l'insorgere delle corrispondenti armoniche di tensione.
Funzionano perciò come compensatori armonici per i carichi non lineari. Essi vanno installati nelle immediate vicinanze del carico distorcente. I pratica le armoniche di corrente dio ordine tre e suoi multipli circolano nel carico e nel reattore e non si propagano nella rete di alimentazione.
Corpo dell'articolo assente

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)