Indice |
Premessa
PS: Beh, che dire? Mi ero completamente dimenticato di un articolo scritto appena sei anni fa sullo stesso tema. È proprio vero: i vecchi finiscono per dire sempre le stesse cose! Ad ogni modo, ormai la frittata è fatta :-(
Abstract
Lo studio di un sistema trifase simmetrico ed equilibrato si riconduce allo studio di un circuito monofase, come noto.
Quando le tensioni sono dissimmetriche ed i carichi squilibrati è ancora possibile riportarsi allo studio di reti monofasi, mediante la scomposizione del sistema dissimmetrico in tre reti simmetriche, denominate rete di sequenza diretta, rete di sequenza inversa e rete di sequenza omopolare (o zero).
Il metodo risulta molto utile nell'analisi delle più importanti dissimmetrie che si verificano negli impianti in conseguenza guasti come interruzioni di fasi e cortocircuiti tra fasi o tra fasi e terra o neutro.
L'articolo è la riedizione di un vecchio articolo in cui sono riportati anche i contenuti teorici, revisionati e con qualche aggiunta, di un altro paio di articoli ( (1, 2).
Terna diretta, inversa, omopolare
Definiamo l'operatore complesso α che, moltiplicato per un vettore lo fa ruotare di  , cioè
, cioè  radianti in senso antiorario, lasciandone immutato il modulo.
radianti in senso antiorario, lasciandone immutato il modulo.

Consideriamo il vettore rappresentativo di una tensione sinusoidale che, arbitrariamente, indicheremo con l'indice 1, dunque  , che chiameremo vettore origine.
, che chiameremo vettore origine.
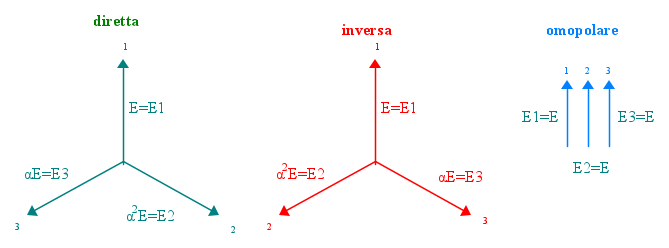
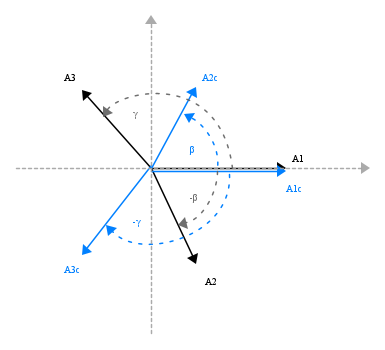
Si definisce terna diretta la terna formata dai tre vettori che si ottengono moltiplicando successivamente per 1,α2,α, il vettore origine; terna inversa quella che si ottiene moltiplicandolo successivamente per 1,α,α2.
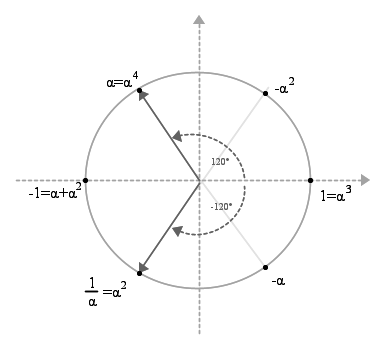
- NB: alcune espressioni da ricordare ed una loro rappresentazione grafica
- 1 + α + α2 = 0
- 1 = α3: α è una delle radici cubiche dell'unità; le altre sono 1 ed α2
- α4 = α
 (la barretta indica il numero complesso coniugato)
(la barretta indica il numero complesso coniugato)

Se le tre tensioni oltre che lo stesso valore efficace hanno anche la stessa fase, la terna delle tensioni si dice omopolare. I tre vettori rappresentativi sono in tal caso uguali e paralleli. La terna omopolare si ottiene moltiplicando sempre per 1 il vettore origine.
Il disegno che segue illustra quanto scritto con  vettore origine.
vettore origine.
Terne dissimmetriche
Quando le tre tensioni non soddisfano le condizioni che definiscono il sistema simmetrico, la terna si dice dissimmetrica.
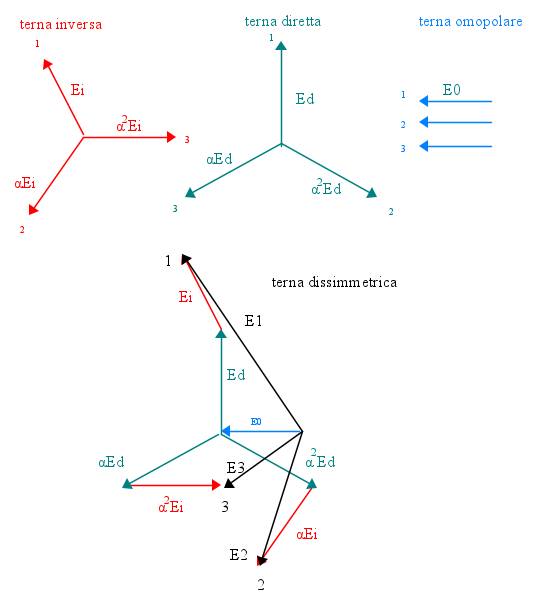
Si può dimostrare che ogni terna dissimmetrica è scomponibile in una terna diretta, una terna inversa ed una terna omopolare.
Indicando rispettivamente con  , i vettori origine delle tre terne, se
, i vettori origine delle tre terne, se  sono i vettori della terna dissimmetrica, si può scrivere:
sono i vettori della terna dissimmetrica, si può scrivere:
![\left\{ \begin{array}{l}
{{\dot E}_1} = {{\dot E}_0} + {{\dot E}_d} + {{\dot E}_i}\\
{{\dot E}_2} = {{\dot E}_0} + {\alpha ^2}{{\dot E}_d} + \alpha {{\dot E}_i} \quad[1]\\
{{\dot E}_3} = {{\dot E}_0} + \alpha {{\dot E}_d} + {\alpha ^2}{{\dot E}_i}
\end{array} \right.](/mediawiki/images/math/1/c/1/1c13e8f7ea60da3bcb4c23d38a3f968e.png)
Le [1] costituiscono un sistema di tre equazioni da cui si possono ricavare le tre incognite  .
.
![\begin{array}{l}
{{\dot E}_0} = \frac{{{{\dot E}_1} + {{\dot E}_2} + {{\dot E}_3}}}{3}\\
{{\dot E}_d} = \frac{{{{\dot E}_1} + \alpha {{\dot E}_2} + {\alpha ^2}{{\dot E}_3}}}{3} \quad[2]\\
{{\dot E}_i} = \frac{{{{\dot E}_1} + {\alpha ^2}{{\dot E}_2} + \alpha {{\dot E}_3}}}{3}
\end{array}](/mediawiki/images/math/3/4/1/341f187bc61000150adee2695e5f4fe1.png)
Note
Il vettore che si ottiene dalle [2] è il primo della terna, cioè il vettore origine.
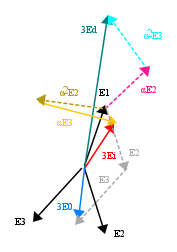
Se come primo vettore della terna dissimmetrica invece di  si considera
si considera  , mantenendo il senso ciclico, il vettore origine ha sempre lo stesso modulo, ma è ruotato di
, mantenendo il senso ciclico, il vettore origine ha sempre lo stesso modulo, ma è ruotato di  in senso orario, il diretto, di
in senso orario, il diretto, di  in senso antiorario, l'inverso. Vediamolo per il
in senso antiorario, l'inverso. Vediamolo per il
diretto



} e si ricordi che α3 = 1


e per l'
inverso

moltiplichiamo numeratore e denominatore per α2


terne coniugate
Se indichiamo con  i componenti simmetrici di una terna di vettori e con
i componenti simmetrici di una terna di vettori e con
 quelli della terna coniugata, esistono le relazioni
quelli della terna coniugata, esistono le relazioni
![\overline {A_0} = \dot A_{\overline 0} \quad \overline {A_d}= \dot A_{\overline i} \quad \overline {A_i}= \dot A_{\overline d}\quad [1a]](/mediawiki/images/math/c/f/1/cf198f5b6751d895b4877afa5f32caeb.png)
Lo scambio tra la componente diretta ed inversa è riconducibile al fatto che la terna dei coniugati ha il senso ciclico invertito, come mostrato nel seguente disegno dove la terna originaria è costituita dai vettori in nero, quella dei coniugati, in blu (per ottenere il coniugato di un vettore si cambia di segno l'angolo)
Ma naturalmente lo si può anche vedere analiticamente tenendo presente le note su α e che il coniugato di un prodotto è il prodotto dei coniugati.

Concatenate e stellate
In un sistema trifase le tensioni concatenate sono quelle esistenti tra due fili; le tensioni stellate quelle esistenti tra uno dei fili ed il polo comune dei tre bipoli che hanno l'altro polo collegato ai tre fili. Il polo comune è detto centro stella.
Numerati i fili con 1,2,3 ed indicata con la lettera O il centro stella, indichiamo con  le tensioni stellate e con
le tensioni stellate e con  le tensioni concatenate.
le tensioni concatenate.
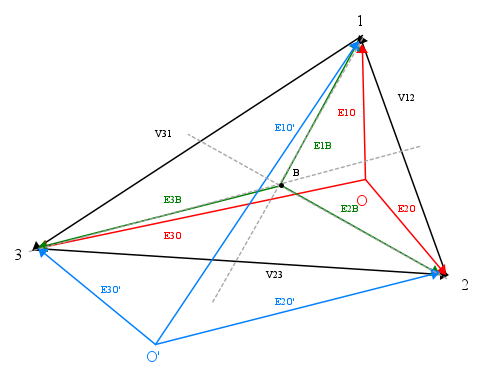
Mentre la terna di tensioni concatenate è unica, sono infinite le possibili terne di tensioni stellate.
Nella figura che segue ne sono rappresentate tre: rossa di centro O, blu di centro O', verde di centro B:quest'ultimo è il baricentro del triangolo (incontro delle mediane, linee tratteggiate)
La componente omopolare è nulla quando la somma dei vettori è nulla.
Quindi le tensioni concatenate di un sistema trifase dissimmetrico hanno comunque sempre componente omopolare nulla.
Per le concatenate vale sempre infatti

Non è così per le tensioni stellate.
Solo la terna di stellate il cui centro stella coincide con il baricentro del triangolo delle concatenate, ha componente omopolare nulla. Infatti si può scrivere

Il baricentro degli estremi dei tre vettori vertici del triangolo, è definito dalle coordinate


I vettori della stella che ha come centro stella il baricentro sono allora dati da

per cui


Le infinite stelle di vettori aventi vertici comuni, hanno come componenti la stessa terna diretta e la stessa terna inversa.
Infatti


 sono uniche perché esiste una sola terna di tensioni concatenate; quindi sono uniche pure
sono uniche perché esiste una sola terna di tensioni concatenate; quindi sono uniche pure  e
e  , che si ricavano dalle precedenti moltiplicando per un fattore costante, mentre la terna delle stellate è qualsiasi.
, che si ricavano dalle precedenti moltiplicando per un fattore costante, mentre la terna delle stellate è qualsiasi.
Le terne stellate che si appoggiano ai vertici del triangolo delle stellate, differiscono perciò per la sola terna omopolare.
Come mostrato più sopra, la terna che ha come centro il baricentro del triangolo, ha componente omopolare nulla.
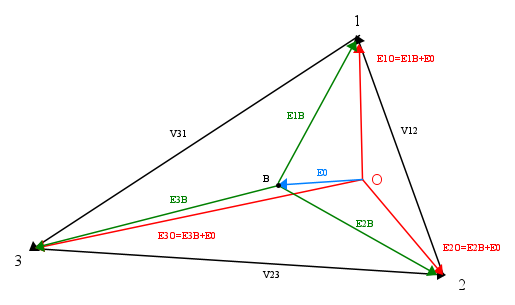
La componente omopolare di ogni altra stella, coincide con il vettore che unisce il centro della stella con il baricentro del triangolo. Ogni stella si ottiene perciò aggiungendo ad ogni vettore della stella pura la componente omopolare, come mostrato nel seguente disegno: E0 è la componente omopolare della stella rossa, la stella verde è la stella purapura
Reti trifase
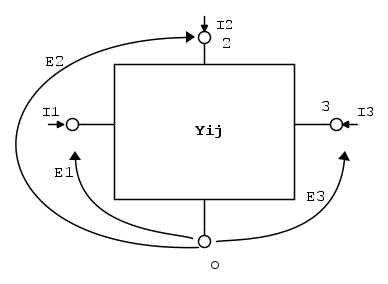
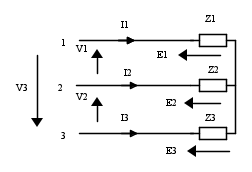
Una rete trifase con neutro accessibile, può essere schematizzata come il triplo bipolo di figura.
La tensione  applicata tra il terminale i ed il comune O, inietta nella rete la corrente
applicata tra il terminale i ed il comune O, inietta nella rete la corrente 
Le relazioni che legano correnti e tensioni sono
![\begin{array}{l}
\dot I_1 = \dot Y_{11} \cdot \dot E_1 + \dot Y_{12} \cdot \dot E_2 + \dot Y_{13} \cdot \dot E_3 \\
\dot I_2 = \dot Y_{21} \cdot \dot E_1 + \dot Y_{22} \cdot \dot E_2 + \dot Y_{23} \cdot \dot E_3 \quad [2]\\
\dot I_3 = \dot Y_{31} \cdot \dot E_1 + \dot Y_{32} \cdot \dot E_2 + \dot Y_{33} \cdot \dot E_3 \\
\end{array}](/mediawiki/images/math/3/b/6/3b6b12985eea6bd4a573958c9a7363a1.png)
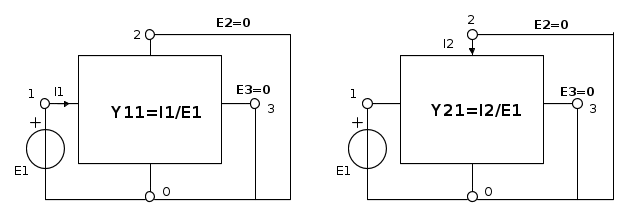
 sono le auto (i = j) e mutue (
sono le auto (i = j) e mutue ( ) ammettenze del triplo bipolo e si determinano alimentando un terminale con un generatore di tensione e cortocircuitando gli altri due
) ammettenze del triplo bipolo e si determinano alimentando un terminale con un generatore di tensione e cortocircuitando gli altri dueIl sistema [2] può essere trasformato nel suo duale
![\begin{array}{l}
\dot E_1 = \dot Z_{11} \dot I_1 + \dot Z_{12} \dot I_2 + \dot Z_{13} \dot I_3 \\
\dot E_2 = \dot Z_{21} \dot I_1 + \dot Z_{22} \dot I_2 + \dot Z_{23} \dot I_3 \quad[2a] \\
\dot E_3 = \dot Z_{31} \dot I_1 + \dot Z_{32} \dot I_2 + \dot Z_{33} \dot I_3 \\
\end{array}](/mediawiki/images/math/6/5/1/65184e96168f886344d6380f863fe84e.png)
Per una scrittura più compatta si può usare la notazione matriciale
![\begin{array}{l}
\left[ {\dot E} \right] = \left[ {\dot Z} \right] \cdot \left[ {\dot I} \right] \\
\left[ {\dot E} \right] = \left[ {\begin{array}{*{20}c}
{\dot E_1 } \\
{\dot E_2 } \\
{\dot E_3 } \\
\end{array}} \right];\left[ {\dot I} \right] = \left[ {\begin{array}{*{20}c}
{\dot I_1 } \\
{\dot I_2 } \\
{\dot I_3 } \\
\end{array}} \right];\left[ {\dot Z} \right] = \left[ {\begin{array}{*{20}c}
{\dot Z_{11} } & {\dot Z_{12} } & {\dot Z_{13} } \\
{\dot Z_{21} } & {\dot Z_{22} } & {\dot Z_{23} } \\
{\dot Z_{31} } & {\dot Z_{32} } & {\dot Z_{33} } \\
\end{array}} \right] \\
\end{array}](/mediawiki/images/math/7/e/a/7ea135ee850d2cceb1b2e79220bc48c8.png)
Lo stesso si poteva fare con il sistema [r.1]
![\begin{array}{l}
\left[ {\dot I} \right] = \left[ {\dot Y} \right] \cdot \left[ {\dot E} \right] \\
\left[ {\dot Y} \right] = \left[ {\begin{array}{*{20}c}
{\dot Y_{11} } & {\dot Y_{12} } & {\dot Y_{13} } \\
{\dot Y_{21} } & {\dot Y_{22} } & {\dot Y_{23} } \\
{\dot Y_{31} } & {\dot Y_{32} } & {\dot Y_{33} } \\
\end{array}} \right]
\end{array}](/mediawiki/images/math/b/0/e/b0e950b8badd4ae677dfd824413e9a5c.png)
Tra la matrice delle impedenze e quella delle ammettenze esiste la relazione:
![\left[ {\dot Y} \right] = \frac{1}{{\left[ {\dot Z} \right]}}](/mediawiki/images/math/b/1/8/b1834fc2f23ecf24e48de1a4e31757f4.png)
Reti simmetriche
La rete è simmetrica se sono uguali tra loro autoammettenze e mutue ammettenze, o le auto e mutue impedenze, quindi se
![\begin{array}{l}
\dot Y_{11} = \dot Y_{22} = \dot Y_{33} \\
\dot Y_{12} = \dot Y_{23} = \dot Y_{31} \quad [3]\\
\dot Y_{21} = \dot Y_{32} = \dot Y_{13} \\
\end{array}](/mediawiki/images/math/e/3/4/e34d06c9c95307775c50063c6c759285.png)
oppure
![\begin{array}{l}
\dot Z_{11} = \dot Z_{22} = \dot Z_{33} \\
\dot Z_{12} = \dot Z_{23} = \dot Z_{31} \quad [3a]\\
\dot Z_{21} = \dot Z_{32} = \dot Z_{13} \\
\end{array}](/mediawiki/images/math/8/f/5/8f532885a7630823759f7a366cb2507e.png)
che, per la notazione matriciale, definiscono una matrice simmetrica rispetto alla diagonale principale.
Inoltre se  la rete si dice reciproca.
la rete si dice reciproca.
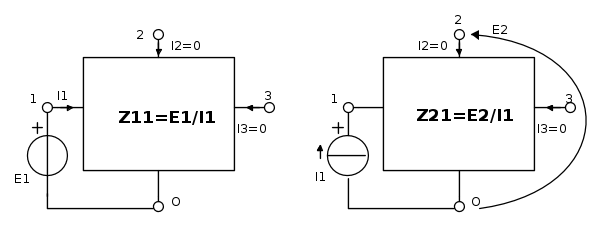
Le auto e mutue impedenze si calcolano secondo gli schemi seguenti
- NB: non sarà superfluo ricordare che gli elementi della matrice inversa non sono, in generale, l'inverso degli elementi della matrice originaria. Vedere questo articolo
Tenendo presenti le relazioni di simmetria, e scomponendo le correnti e le tensioni nelle loro componenti simmetriche nel sistema [2] si ottiene
![\begin{array}{l}
\dot I_0 = \dot Y_0 \cdot \dot E_0 \\
\dot I_d = \dot Y_d \cdot \dot E_d \quad [3b]\\
\dot I_i = \dot Y_i \cdot \dot E_i \\
\end{array}](/mediawiki/images/math/e/5/7/e5703bfcc954d1b086c3796c1fad29fb.png)
dove si è posto

Questo permette di definire anche, per ogni rete simmetrica, oltre alle ammettenze, le impedenze alle sequenze zero, diretta ed inversa

per cui le [3b] diventano
![\begin{array}{l}
\dot E_0 = \dot Z_0 \cdot \dot I_0 \\
\dot E_d = \dot Z_d \cdot \dot I_d \quad [3c]\\
\dot E_i = \dot Z_i \cdot \dot I_i \\
\end{array}](/mediawiki/images/math/1/2/b/12b4f2745815fbf462fd8cc1bcada8d1.png)
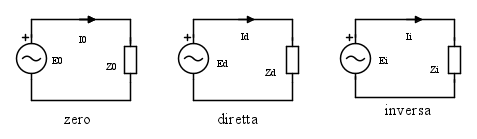
Le impedenze di sequenza sono misurabili applicando separatamente alla rete una terna di sequenza zero, una terna di sequenza diretta, un terna di sequenza inversa. Analiticamente si ricavano con

- Le [3b],[3c] mostrano che in una rete simmetrica le componenti simmetriche delle tensioni danno luogo solo a correnti della stessa sequenza.
Quindi una rete simmetrica alimentata da una terna dissimmetrica si può scomporre nelle tre
Reti di sequenza
Sono i tre bipoli definiti dalle [3b] o [3c]
Le equazioni relative ai tre bipoli forniscono tre relazioni per le sei componenti di sequenza.
Per ricavar le sei componenti di sequenza occorrono altre tre equazioni, che in genere sono definite dalle condizioni in cui si trova il sistema trifase. Lo si vedrà nello studio dei guasti.
Naturalmente ciò presuppone la conoscenza delle impedenze di sequenza della rete per le quali valgono le seguenti osservazioni.
- Le impedenze alla sequenza inversa e diretta sono uguali se
 . In particolare questo si verifica per per tutte le reti che non contengono parti in movimento.
. In particolare questo si verifica per per tutte le reti che non contengono parti in movimento.
- Se per ogni
 si ha
si ha  la rete è detta reciproca e, per quanto detto, lo può essere solo se non esistono parti in movimento.
la rete è detta reciproca e, per quanto detto, lo può essere solo se non esistono parti in movimento.
- È immediato constatare che una stella con tre impedenze identiche costituisce una rete simmetrica. L'autoammettenza (autoimpedenza) comune è l'ammettenza (impedenza) di un ramo.
- Le mutue ammettenze sono nulle se non vi è accoppiamento induttivo e/o capacitivo.
- Quando il terminale comune O non esiste od è inaccessibile, l'impedenza alla sequenza zero è infinita (
 )
)
- Se non esistono accoppiamenti cioè se
 per
per  , le impedenze alle sequenze sono tutte uguali all'inverso dell'unica autoammettenza:
, le impedenze alle sequenze sono tutte uguali all'inverso dell'unica autoammettenza: . La rete in tal caso è riconducibile ad una stella di tre impedenze uguali. Vale ovviamente il viceversa: tre impedenze uguali a stella costituiscono una rete simmetrica e le tre impedenze di sequenza sono uguali all'impedenza di un ramo.
. La rete in tal caso è riconducibile ad una stella di tre impedenze uguali. Vale ovviamente il viceversa: tre impedenze uguali a stella costituiscono una rete simmetrica e le tre impedenze di sequenza sono uguali all'impedenza di un ramo.
- Le normali linee trifase, nonché trasformatori ed alternatori, sono considerati elementi simmetrici, come pure i carichi come i motori asincroni.
- Si assume anche in genere che le tre fasi siano in condizioni di simmetria rispetto al terreno e rispetto al neutro, sia che ci siano effettivi collegamenti a centri stella di componenti della rete, sia che il collegamento sia dovuto alle capacità parassite d'esercizio.
Reti non simmetriche
Stella non simmetrica
Se non sono soddisfatte le condizioni [3] o [3a] la rete non è simmetrica e può essere rappresentata da tre impedenze diverse collegate a stella.
Le equazioni per la stella sono

Scomponiamo secondo le [1] sia le tre tensioni che le tre correnti e sostituiamo nelle equazioni della stella.
Dopo alcune elaborazioni si ottiene
![\begin{array}{l}
\dot E_0 = \dot Z_0^* \cdot \dot I_0 + \dot Z_i^* \cdot\dot I_d + \dot Z_d^* \cdot\dot I_i \\
\dot E_d = \dot Z_d^* \cdot\dot I_0 + \dot Z_0^* \cdot\dot I_d + \dot Z_i^* \cdot\dot I_i \quad[4]\\
\dot E_i = \dot Z_i^* \cdot\dot I_0 + \dot Z_d^* \cdot\dot I_d + \dot Z_0^* \cdot\dot I_i \\
\end{array}](/mediawiki/images/math/b/1/8/b189078e3343dc066da85575b218e518.png)
dove si è posto
![\begin{array}{l}
\dot Z_d^* = \frac{{\dot Z_1 + \alpha \dot Z_2 + \alpha ^2 \dot Z_3 }}{3} \\
\dot Z_i^* = \frac{{\dot Z_1 + \alpha ^2 \dot Z_2 + \alpha \dot Z_3 }}{3} \quad [5]\\
\dot Z_0^* = \frac{{\dot Z_1 + \dot Z_2 + \dot Z_3 }}{3} \\
\end{array}](/mediawiki/images/math/6/7/0/6705096375d0d911e6f506d99ed35c5e.png)
Innanzitutto notiamo che, contrariamente alle reti simmetriche, ogni sequenza presente nelle tensioni può far circolare correnti di ogni sequenza.
Osserviamo poi che le componenti  ed
ed  sono determinate una volta che siano note le tensioni concatenate, come mostrato in precedenza.
sono determinate una volta che siano note le tensioni concatenate, come mostrato in precedenza.
Anche la componente omopolare delle correnti è nota: infatti  essendo nulla la somma delle tre correnti.
essendo nulla la somma delle tre correnti.
Le precedenti equazioni costituiscono perciò un sistema di tre equazioni nelle incognite 
![\begin{array}{l}
\dot Z_i^* \dot I_d + \dot Z_d^* \dot I_i -\dot E_0=0\\
\dot Z_0^* \dot I_d + \dot Z_i^* \dot I_i = \dot E_d \quad \quad \quad[6]\\
\dot Z_d^* \dot I_d + \dot Z_0^* \dot I_i = \dot E_i \\
\end{array}](/mediawiki/images/math/2/1/f/21fd6c9ca1c394d80cea0ac21016297a.png)
Triangolo non simmetrico
Una rete non simmetrica può essere anche rappresentata da tre impedenze diverse collegate a triangolo
È il duale del precedente. Le ammettenze sostituiscono le impedenze. Le correnti di fase  svolgono il ruolo delle tensioni di fase della stella.
svolgono il ruolo delle tensioni di fase della stella.
La componente omopolare delle tensioni concatenate è nulla.
Indicate dunque con  e
e  le componenti simmetriche delle concatenate, potremo scrivere le equazioni per ricavare
le componenti simmetriche delle concatenate, potremo scrivere le equazioni per ricavare 
![\begin{array}{l}
\dot Y_i^* \dot V_d + \dot Z_d^* \dot V_i -\dot J_0=0\\
\dot Y_0^* \dot V_d + \dot Z_i^* \dot V_i = \dot J_d \quad \quad \quad[7]\\
\dot Y_d^* \dot V_d + \dot Z_0^* \dot V_i = \dot J_i \\
\end{array}](/mediawiki/images/math/c/0/8/c08ab50217abb2b986e1f13714a936d6.png)
La potenza
La
potenza complessa
di un bipolo è il prodotto del numero complesso che rappresenta la tensione e del coniugato del numero complesso che rappresenta la corrente.
La potenza complessa assorbita da un sistema trifase è la somma delle potenze complessa delle singole fasi. Quindi

Sostituendo le espressioni relative alla scomposizione delle due terne si arriva alla

che equivale a dire che sia la potenza attiva che la reattiva sono la somma delle potenze proprie di ogni componente simmetrica

L'espressione precedente ci dice anche che nei siatemi a neutro isolato dove  , le potenze assorbite non dipendono dal potenziale del centro stella.
, le potenze assorbite non dipendono dal potenziale del centro stella.
Aggiungiamo qualche osservazione sulla
Potenza fluttuante
La potenza istantanea in un sistema monofase, prodotto dei valori istantanei di tensione e corrente, si compone di un valore medio, che è la potenza attiva P, cui si sovrappongono i valori di una sinusoide di ampiezza pari alla potenza apparente e di pulsazione doppia di quella di tensione e corrente. Questa sinusoide è la potenza fluttuante. Quindi

con
S = VI

essendo


Per qualche particolare di calcolo si può vedere questo articolo.
In un sistema trifase la potenza totale istantanea è la somma delle potenze delle tre fasi e per i sisteme simmetrici ed equilibrati si verifica che la potenza fluttuante è nulla, quindi che la potenza istantanea è una costante che coincide con la potenza attiva.
La potenza fluttuante può essere rappresentata con un vettore rotante ricavato dal prodotto dei vettori rotanti di tensione e di corrente, altrimenti detti fasori. E' infatti il fasore a corrispondere alla funzione sinusoidale che rappresenta le grandezze. I fasori di tensione e corrente sono espressi da


dove
 e
e 
Il prodotto tra i fasori è dato da
 , con
, con  ,
,
che è un vettore rotante a velocità angolare ( o pulsazione) doppia di quella comune a tensione e corrente. Tale fasore rappresenta la potenza fluttuante, ed ha modulo pari alla potenza apparente.
- nota:potrebbe sembrare di poter scrivere che
 è il coniugato della potenza complessa, ma il valore trovato dipende dal sistema di riferimento per le fasi. Per essere più generali, dobbiamo scrivere
è il coniugato della potenza complessa, ma il valore trovato dipende dal sistema di riferimento per le fasi. Per essere più generali, dobbiamo scrivere

- nella trattazione precedente si è assunto

La potenza fluttuante trifase è la somma di quella delle tre fasi

Sostituendo ai vettori la loro scomposizione nelle componenti simmetriche, sviluppando i calcoli, si arriva alla

che mostra che quando  la potenza fluttuante è nulla, cioè la potenza istantanea è costante, se non ci sono correnti di sequenza diversa da quella delle tensioni.
la potenza fluttuante è nulla, cioè la potenza istantanea è costante, se non ci sono correnti di sequenza diversa da quella delle tensioni.
Per la misura della potenza attiva con neutro accessibile si possono usare tre wattmetri inseriti tra i fili ed il neutro. Se il neutro non è accessibile, quindi in un sistema accessibile, si usano due wattmetri in inserzione Aron.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)