ElectroYou - la comunità dei professionisti del mondo elettrico

Vai a: navigazione, ricerca

Il qui presente articolo, nasce in risposta ad una domanda postami in privato, da un utente del forum. Poiché sprovvisto di tempo. Al tempo, temo di aver risposto frettolosamente, quindi cerco di rimediare.

La domanda: Ho visto che ci sono esercizi dove i flussi dei campi magnetici hanno anche la parte relativa alla mutua induzione ed altri dove non ce l'hanno e questo spesso viene assunto all'inizio dell'esercizio stesso senza che il testo specifichi se M=0 H o meno. Quindi vorrei sapere, quand'è che ho mutua induzione e devo calcolare M e quando no? In teoria se ho due o più avvolgimenti sui quali scorrono delle correnti di intesità i diverse dovrei avere mutua induzione (o comunque verificare se c'è o meno) perché è come se avessi due circuiti distinti. Mentre posso in genere dire che se ho due o più avvolgimenti sui quali scorre la stessa intensità di corrente, non ho mutua induzione perché la mutua induzione è quella che si crea tra circuiti distinti. È giusto?

Indice

1 Un esercizio di riscaldamento
- 1.1 Svolgimento
- 1.2 Osservazioni
2 Il problema
3 Simulazione campo di induzione magnetica
4 La soluzione
5 Bibliografia

Un esercizio di riscaldamento

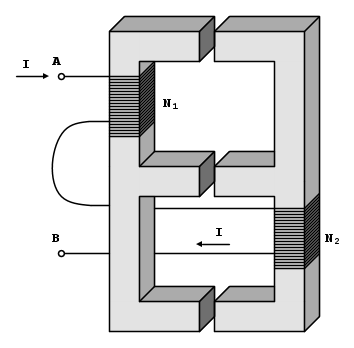
Calcolare il coefficiente di autoinduzione del bipolo A-B nell’ ipotesi di trascurare le riluttanze dei tratti in ferro e i flussi dispersi. La lunghezza t del traferro è pari a 1 mm, la sezione trasversale del nucleo ferromagnetico S è pari a 4 cm², N₁=100 e N₂=200.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Svolgimento

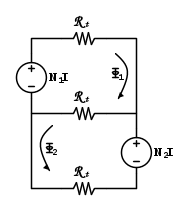
Disegniamo il circuito elettrico equivalente.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

dove

$\mathfrak{R_t} = \frac{t}{\mu_0 \cdot S}=\frac{1 \cdot 10^{-3}}{4\pi \cdot 10^{-7} \times 4 \cdot 10^{-4}} \simeq 2 \; \text{MH}^{-1}$

le equazioni sono

$\left\{\begin{matrix} N_1I=2 \; \mathfrak{R_t} \cdot \Phi_1 + \mathfrak{R_t} \cdot \Phi_2 \\ N_2I=\mathfrak{R_t} \cdot \Phi_1 + 2 \; \mathfrak{R_t} \cdot \Phi_2 \end{matrix}\right.$

invertiamo la matrice

$\begin{bmatrix} \Phi_1 \\ \Phi_2 \end{bmatrix} = \frac{1}{4 \; \mathfrak{R_t}^2-\mathfrak{R_t}^2} \begin{bmatrix} 2 \; \mathfrak{R_t} & -\mathfrak{R_t} \\ -\mathfrak{R_t} & 2 \; \mathfrak{R_t} \end{bmatrix} \begin{bmatrix} N_1I \\ N_2I \end{bmatrix}$

da cui

$\Phi_1 = \frac{2 \; N_1}{3 \; \mathfrak{R_t}}I - \frac{N_2}{3 \; \mathfrak{R_t}}I$

$\Phi_2 = \frac{2 \; N_2}{3 \; \mathfrak{R_t}}I - \frac{N_1}{3 \; \mathfrak{R_t}}I$

Notiamo che il flusso concatenato con i solenoidi costituenti il dipolo A-B non è uguale in entrambi gli avvolgimenti.

$\Phi_{c1} = N_1 \cdot \Phi_1 = \frac{2 \; N_1^2}{3 \; \mathfrak{R_t}}I - \frac{N_1 \; N_2}{3 \; \mathfrak{R_t}}I$

$\Phi_{c2} = N_2 \cdot \Phi_2 = \frac{2 \; N_2^2}{3 \; \mathfrak{R_t}}I - \frac{N_1 \; N_2}{3 \; \mathfrak{R_t}}I$

da queste due ultime relazioni evinciamo

$L_1 = \frac{2 \; N_1^2}{3 \; \mathfrak{R_t}} = 3.\overline{3} \; \text{mH}$

$L_2 = \frac{2 \; N_2^2}{3 \; \mathfrak{R_t}} = 13.\overline{3} \; \text{mH}$

$M = \frac{N_1 \; N_2}{3 \; \mathfrak{R_t}} = 3.\overline{3} \; \text{mH}$

È piuttosto evidente, la presenza di un (rilevante) accoppiamento magnetico tra i due induttori, pertanto sarebbe immenso l'errore che commetteremo, considerando

$L = L 1 + L 2$

dove L è il coefficiente di autoinduzione del dipolo A-B.

Proviamo a seguire un'altra strada, il flusso concatenato totale, attraverso i due solenoidi è la somma dei singoli flussi concatenati

$Φ c = Φ c 1 + Φ c 2$

da cui

$L=\frac{\Phi_c}{I}= \frac{2 \; N_1^2}{3 \; \mathfrak{R_t}} + \frac{2 \; N_2^2}{3 \; \mathfrak{R_t}} - 2 \frac{N_1 \; N_2}{3 \; \mathfrak{R_t}} = 10 \; \text{mH}$

Osservazioni

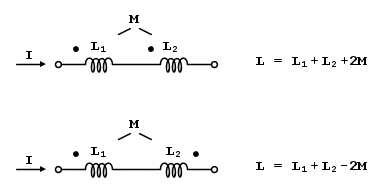
Ora è facile osservare, che

$L = L_1 + L_2 - 2 \; M$

Questa relazione è abbastanza generale, a meno del segno davanti alla mutua, questo dipende dal senso di avvolgimento delle spire.

Basandosi sulla convenzione dei puntini, si ha

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Il problema

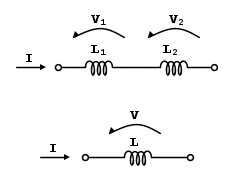
Nello studio dei circuiti elettrici, ci è stato insegnato che due induttori, elettricamente in serie, si comportano come un solo induttore, avente coefficiente di autoinduzione, pari alla somma delle due singole induttanze.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

$L = L 1 + L 2$

e

$V = V 1 + V 2$

Quest'equivalenza si dimostra facilmente, sulla base della relazione caratteristica dell'induttore.

Ma come si è visto nell'esercizio precedente, questa relazione non è sempre vera. Allora quali sono le condizioni di validità della suddetta?

Per capire un po meglio il fenomeno, facciamo qualche simulazione.

Simulazione campo di induzione magnetica

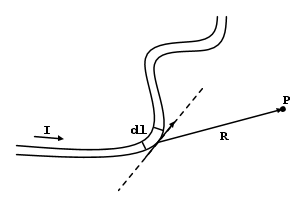
Lo strumento base, per il calcolo del campo di induzione magnetica, generato in un punto, da una distribuzione di corrente è la legge di Biot-Savart, che riassumo in breve.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

$dB = \frac{\mu_0}{4\pi}\frac{I \; dl \times R}{R^3}$

Non esplicito i vettori poiché desumibili dagli operatori.

Generato da una spira

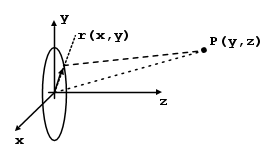
Nota la legge di Biot-Savart, andiamo ad analizzare una geometria piuttosto semplice, comunque di notevole interesse, essendo l'elemento costitutivo dei solenoidi, ossia la spira.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

La spira, ha una simmetria cilindrica, quindi al fine di determinare il campo B(x,y,z), non è necessario studiare il problema effettivamente in 3D, possiamo invece, sezionare la spira con un piano yz e studiare il campo B(y,z).

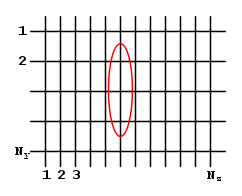
Per integrare numericamente la legge di Biot - Savart, è necessario discretizzare lo spazio attorno alla spira, chiamiamo:

$N y$ il numero di iterazioni lungo l'asse y.
$N z$ il numero di iterazioni lungo l'asse z.

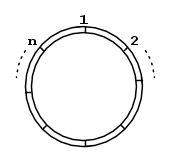
Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

È inoltre necessario discretizzare la spira stessa, chiamiamo $n$ il numero di elementini $d l$ in cui suddividiamo la spira.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Ora abbiamo tutti gli strumenti per scrivere un

Algoritmo

% definizmo la spira
phi= -pi: 2*pi/n:pi
 
rx=r*cos(\phi)
ry=r*sin(\phi)


% ciclo lungo la griglia spaziale
for z = -L:2*L/(Nz-1):L
for y=-2*r:4*r/(Ny-1):2*r

    % per ogni y,z azzeriamo B vettore
    Bx(y,z)=0
    By(y,z)=0
    Bz(y,z)=0
    
    % ciclo lungo la spira
    for i=1:n-1

       % calcolo componenti dl
       dx=rx(i+1)-rx(i)
       dy=ry(i+1)-ry(i)

       % calcolo distanza tra dl e P
       Rx=-0.5*(rx(i+1)+rx(i))
       Ry=y-0.5*(ry(i+1)+ry(i))
       Rz=z

       % modulo della distanza
       R=sqrt(Rx^2+Ry^2+Rz^2)

       % calcolo di dl vettor R
       Xcross=dy*Rz
       Ycross=-dx*Rz
       Zcross=dx*Ry-dy*Rx

       % legge di Biot-Savart
       Bx(y,z)=Bx(y,z)+((u0*I*Xcross)/(4*pi*R^3))
       By(y,z)=By(y,z)+((u0*I*Ycross)/(4*pi*R^3))
       Bz(y,z)=Bz(y,z)+((u0*I*Zcross)/(4*pi*R^3))
    end
end
end

A questo punto è facile tradurre l'algoritmo in qualche linguaggio di alto livello. Segue il risultato di una simulazione fatta con matlab.

campo spira.jpg

Generato da un solenoide

Se il solenoide ha una densità di spire considerevole, si può assumere con buona approssimazione, come fosse costituito da una serie di anelli, anziché come un'elica cilindrica.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Questo rende la simulazione molto simile a quella della spira base. Di fatto, dobbiamo semplicemente aggiungere un ciclo, che valuti il contributo di ogni spira.

Segue direttamente il codice matlab.

clc;
clear all;

N=100;
L = 10;
r=1;
I=1;
u0=4*pi*1e-7;
 
Nz=75;
Ny=25;
n=25;

phi=-pi:2*pi/n:pi;

rx=r*cos(phi);
ry=r*sin(phi);
rz=-L/2:L/N:L/2;

zp(1:Nz)=-L:2*L/(Nz-1):L;    
yp(1:Ny)=-2*r:4*r/(Ny-1):2*r;   

Y(1:Ny,1:Nz)=0; 
Z(1:Ny,1:Nz)=0;

for i=1:Nz
    Z(:,i)=zp(i);
end
for i=1:Ny
    Y(i,:)=yp(i);
end

for z=1:Nz
for y=1:Ny

    Bx(y,z)=0;
    By(y,z)=0;
    Bz(y,z)=0;

    for j=1:N
    for i=1:n-1

        dx=rx(i+1)-rx(i);
        dy=ry(i+1)-ry(i);

        Rx=-0.5*(rx(i+1)+rx(i));
        Ry=Y(y,z)-0.5*(ry(i+1)+ry(i));
        Rz=Z(y,z)-rz(j);

        R=sqrt(Rx^2+Ry^2+Rz^2);

        Xcross=dy*Rz;
        Ycross=-dx*Rz;
        Zcross=dx*Ry-dy*Rx;

        Bx(y,z)=Bx(y,z)+((u0*I*Xcross)/(4*pi*R^3));
        By(y,z)=By(y,z)+((u0*I*Ycross)/(4*pi*R^3));
        Bz(y,z)=Bz(y,z)+((u0*I*Zcross)/(4*pi*R^3));

    end
    end
end
end

plot([-L/2 L/2 L/2 -L/2 -L/2],[-r -r r r -r],'r'), hold on;
quiver(zp,yp,Bz,By)
axis([-L L -2*r 2*r])
xlabel('Z-axis','fontsize',14)
ylabel('Y-axis','fontsize',14)
title('B-field Vector flow','fontsize',14)

Che produce.

induttore.jpg

Come si nota, la quasi totalità del campo si trova all'interno del solenoide, con dei leggeri effetti di bordo che non fanno molta strada.

Solenoide avvolto in cilindro ferromagnetico

Vediamo ora cosa succede se avvolgiamo le nostre spire, in un cilindro idealmente infinito, di materiale ferromagnetico, ad' esempio il ferro.

induttorefe.jpg

Da quest'ultima imagine, vediamo che tutto il campo si trova all'interno del cilindro ferromagnetico, praticamente al di fuori di esso non è presente campo B.

La soluzione

Ora che abbiamo le idee leggermente più chiare, possiamo trarre qualche conclusione.

Due solenoidi, elettricamente in serie, sufficientemente distanti tra loro e non connessi da tubi di flusso magnetico, possono considerarsi magneticamente disaccoppiati.

Quindi il coefficiente di mutua induzione sarà nullo. $M = 0$ .

Dalle relazioni

$L=L_1+L_2 \pm 2M$

si ottiene

$L = L 1 + L 2$

sotto tali condizioni è quindi valida la relazione caratteristica dell'induttore

$v=L \frac{di}{dt}$

Due solenoidi, elettricamente in serie, sufficientemente vicini tra loro e/o connessi da un tubo di flusso magnetico, sono magneticamente accoppiati.

Si avrà in generale $M > 0$ .

Bibliografia

L'induttore mir(autore)

Circuiti elettrici di Charles K. Alexander (Autore), Matthew N. O. Sadiku (Autore), C. Gerardi (a cura di), P. Gubian (a cura di)

Elementi di elettrotecnica generale – 1997 di Giovanni Someda (Autore)

Circuiti Magnetici A. Fanni(Autore)

ElectroYou - la comunità dei professionisti del mondo elettrico

Mutuo accoppiamento tra induttori in serie

Indice

Un esercizio di riscaldamento

Svolgimento

Osservazioni

Il problema

Simulazione campo di induzione magnetica

Generato da una spira

Algoritmo

Generato da un solenoide

Solenoide avvolto in cilindro ferromagnetico

La soluzione

Bibliografia

Inserisci un commento

Argomenti correlati

Tag Cloud

Informazioni

Seguici

Pubblicità

Credits