A complemento di quanto descritto nell'articolo [1], voglio qui descrivere un fenomeno di instabilità che si verifica negli attuatori capacitivi: oltre a rappresentare un interessante esercizio di fisica (ehm, per due o tre lettori, diciamo), il fenomeno ha una certa rilevanza per la realizzazione degli attuatori capacitivi integrati [2]. Chi è matematicamente debole di cuore, dopo l'Introduzione, può saltare alle Conclusioni.
Indice |
1 Introduzione
Un attuatore capacitivo è un condensatore che sfrutta la forza elettrostatica agente sulle armature per generare uno spostamento dipendente dalla tensione di comando applicata.
Si consideri allora un dispositivo costituito da due armature piane e parallele di area  , poste perpendicolarmente ad un generico asse
, poste perpendicolarmente ad un generico asse  : un'armatura sia fissa, l'altra mobile nella direzione dell'asse
: un'armatura sia fissa, l'altra mobile nella direzione dell'asse  e solidale a una molla di richiamo di costante elastica
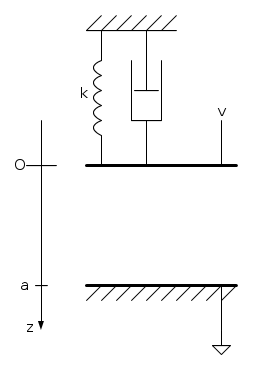
e solidale a una molla di richiamo di costante elastica  ; il possibile moto oscillatorio dell'armatura mobile sia frenato da uno smorzatore viscoso (fig. 1).
; il possibile moto oscillatorio dell'armatura mobile sia frenato da uno smorzatore viscoso (fig. 1).
Sia  la distanza tra le armature quando la tensione applicata all'attuatore è nulla e la molla è in posizione di riposo; in tale condizione, si scelgano l'origine e il verso dell'asse
la distanza tra le armature quando la tensione applicata all'attuatore è nulla e la molla è in posizione di riposo; in tale condizione, si scelgano l'origine e il verso dell'asse  in modo che le coordinate dell'armatura mobile e dell'armatura fissa siano rispettivamente
in modo che le coordinate dell'armatura mobile e dell'armatura fissa siano rispettivamente  e
e  (fig. 1).
(fig. 1).
Supponendo le due armature immerse in aria (permettività relativa  ), esse formano un condensatore di capacità (trascurando gli effetti ai bordi)
), esse formano un condensatore di capacità (trascurando gli effetti ai bordi)

dove  è la costante elettrica. La precedente espressione può essere scritta in funzione del rapporto
è la costante elettrica. La precedente espressione può essere scritta in funzione del rapporto  come
come

con  ; la grandezza
; la grandezza  che compare a denominatore nella (2) rappresenta la separazione tra le armature normalizzata rispetto ad
che compare a denominatore nella (2) rappresenta la separazione tra le armature normalizzata rispetto ad  .
.
Applicando all'attuatore una tensione di comando  , l'armatura mobile è attirata verso quella fissa dalla forza elettrostatica
, l'armatura mobile è attirata verso quella fissa dalla forza elettrostatica  con [1, eq. (9 bis)]
con [1, eq. (9 bis)]

Anche questa espressione può essere scritta in funzione di  :
:

dove

è la forza tra le armature quando  .
.
La forza totale  agente sull'armatura mobile è la somma della forza
agente sull'armatura mobile è la somma della forza  e della forza antagonista
e della forza antagonista  generata dalla molla; la componente
generata dalla molla; la componente  della forza totale è
della forza totale è

dove  denota la componente
denota la componente  di
di  .
.
I punti di equilibrio del sistema sono le soluzioni (reali e con  compreso tra 0 e 1) dell'equazione
compreso tra 0 e 1) dell'equazione  . L'esistenza di eventuali punti di equilibrio e la loro stabilità verranno discusse nel prossimo paragrafo.
. L'esistenza di eventuali punti di equilibrio e la loro stabilità verranno discusse nel prossimo paragrafo.
2 Punti di equilibrio
L'espressione (6) può essere normalizzata rispetto alla forza  :
:

con

Poiché le equazioni  e
e  hanno le stesse soluzioni, nel prosieguo ci si riferirà soltanto a quest'ultima. Il coefficiente
hanno le stesse soluzioni, nel prosieguo ci si riferirà soltanto a quest'ultima. Il coefficiente  che compare nella (7) rappresenta il rapporto tra i moduli della forza elettrostatica in
che compare nella (7) rappresenta il rapporto tra i moduli della forza elettrostatica in  e della forza antagonista in
e della forza antagonista in  ; come si vedrà, esso è un parametro discriminante le soluzioni dell'equazione
; come si vedrà, esso è un parametro discriminante le soluzioni dell'equazione  .
.
Per  l'equazione
l'equazione  è equivalente a
è equivalente a

Per la regola dei segni di Cartesio, le radici1 reali e positive della (9) sono una o tre, e non ci sono soluzioni negative (questo esclude la possibilità di avere  ). Si osservi, allora, che il polinomio
). Si osservi, allora, che il polinomio  comparente nella (9) ha un massimo relativo in
comparente nella (9) ha un massimo relativo in  e un minimo relativo in
e un minimo relativo in  ; nel massimo tale funzione vale 4/27: in base alla precedente osservazione, se
; nel massimo tale funzione vale 4/27: in base alla precedente osservazione, se  , l'equazione (9) non può avere radici reali comprese tra 0 e 1 (ha due radici complesse e una radice reale, maggiore di 1). In questo caso, l'attuatore non ha punti di equilibrio e l'armatura mobile collassa contro quella fissa (pull-in2); la tensione per cui
, l'equazione (9) non può avere radici reali comprese tra 0 e 1 (ha due radici complesse e una radice reale, maggiore di 1). In questo caso, l'attuatore non ha punti di equilibrio e l'armatura mobile collassa contro quella fissa (pull-in2); la tensione per cui  è la tensione di pull-in
è la tensione di pull-in

La forza normalizzata  [eq. (7)] può, quindi, essere più semplicemente espressa in funzione della tensione normalizzata
[eq. (7)] può, quindi, essere più semplicemente espressa in funzione della tensione normalizzata  :
:

con

La figura 2 mostra il grafico delle due curve  e
e  per tre differenti valori di
per tre differenti valori di  e per
e per  : in tale intervallo, le eventuali intersezioni delle due curve sono soluzioni dell'equazione
: in tale intervallo, le eventuali intersezioni delle due curve sono soluzioni dell'equazione  e, pertanto, punti di equilibrio dell'attuatore. Per
e, pertanto, punti di equilibrio dell'attuatore. Per  , in accordo con quanto visto sopra, non ci sono intersezioni. Per
, in accordo con quanto visto sopra, non ci sono intersezioni. Per  , c'è una sola intersezione in
, c'è una sola intersezione in  dove la (9) ha una radice doppia (la terza radice reale è, come prima, maggiore di 1). Per
dove la (9) ha una radice doppia (la terza radice reale è, come prima, maggiore di 1). Per  ci sono, invece, ben due intersezioni (
ci sono, invece, ben due intersezioni ( e
e  nell'esempio di figura (2).
nell'esempio di figura (2).
Al fine di valutare la stabilità dei punti di equilibrio per  , osserviamo, innanzitutto, che i due punti sono uno minore e l'altro maggiore di 1/3 (fig. 2); assumiamo, senza perdere di generalità,
, osserviamo, innanzitutto, che i due punti sono uno minore e l'altro maggiore di 1/3 (fig. 2); assumiamo, senza perdere di generalità,  e
e  . La stabilità di un generico punto di equilibrio
. La stabilità di un generico punto di equilibrio  può essere determinata analizzando il segno della derivata
può essere determinata analizzando il segno della derivata

Se  l'equilibrio è stabile: un piccolo spostamento
l'equilibrio è stabile: un piccolo spostamento  dell'armatura mobile dà infatti origine a una forza
dell'armatura mobile dà infatti origine a una forza  tendente a opporsi allo spostamento; viceversa, se
tendente a opporsi allo spostamento; viceversa, se  , un piccolo spostamento dall'equilibrio dà origine a una forza concorde con esso.
, un piccolo spostamento dall'equilibrio dà origine a una forza concorde con esso.
Poiché per entrambi i punti  , moltiplicando la (13) per
, moltiplicando la (13) per  si ottiene una grandezza avente lo stesso segno di
si ottiene una grandezza avente lo stesso segno di  :
:

È facile verificare che quest'ultima equazione è equivalente a
![\begin{align}
(1-\zeta_i)f^\prime(\zeta_i) &= 2\left[\frac{f_0(\tilde{v})}{(1-\zeta_i)^2}-\zeta_i\right]+3\zeta_i-1 && \\
&= 2f(\tilde{v},\zeta_i)+3\zeta_i-1 &&\text{dalla (11)} \\
&= 3\zeta_i-1 &&\text{visto che}\ f(\tilde{v},\zeta_i)=0
\end{align}](/mediawiki/images/math/a/6/c/a6c2298a42d1488201cd16c05c1824f1.png)
In conclusione  se e solo se
se e solo se  (ossia
(ossia  ): l'unico punto di equilibrio stabile è allora
): l'unico punto di equilibrio stabile è allora  (si può anche vedere dalla fig. 2: come?).
(si può anche vedere dalla fig. 2: come?).
Riassumendo, se si applica una tensione  all'attuatore capacitivo di figura 1 si possono avere due casi.
all'attuatore capacitivo di figura 1 si possono avere due casi.
- Se
 (
( ), l'armatura mobile viene attirata verso il punto di equilibrio stabile con
), l'armatura mobile viene attirata verso il punto di equilibrio stabile con  . La relazione tra la separazione normalizzata
. La relazione tra la separazione normalizzata  e la tensione normalizzata
e la tensione normalizzata  è illustrata nella figura 3 sotto. La distanza minima tra le armature raggiungibile prima del pull-in è
è illustrata nella figura 3 sotto. La distanza minima tra le armature raggiungibile prima del pull-in è  .
.
- Se
 (
( ), non ci sono punti di equilibrio stabile e l'attuatore collassa (pull-in).
), non ci sono punti di equilibrio stabile e l'attuatore collassa (pull-in).
3 Conclusioni
In un attuatore capacitivo, una molla è utilizzata per generare una forza antagonista che si opponga alla forza elettrostatica che agisce sull'armatura mobile. Applicando una tensione all'attuatore capacitivo, l'armatura mobile dovrebbe avvicinarsi all'armatura fissa fino a che la forza di richiamo non bilancia la forza elettrostatica. La forza elettrostatica, però, non rimane costante al variare della distanza tra le armature, anzi, a parità di tensione, aumenta a mano a mano che le due armature si avvicinano: la forza di richiamo generata dalla molla (supposta lineare) potrebbe allora non essere sufficiente per equilibrare la forza elettrostatica, e l'analisi svolta al paragrafo 2 ci dice che è proprio così. Se la tensione applicata all'attuatore supera un certo valore critico, la tensione di pull-in, la forza di richiamo non è sufficiente a bilanciare la forza elettrostatica e l'attuatore collassa.
Note
- La (9) è un'equazione algebrica di grado 3 risolvibile in forma chiusa con funzioni elementari. Tale soluzione è però un po' involuta; può essere preferibile, allora, risolvere la (9) con metodi numerici, e così è stato fatto per tracciare il grafico di figura 3.
- Il verbo inglese pull-in ha diversi significati; il più vicino al fenomeno qui analizzato è probabilmente quello di arrivare a una fermata (di un bus, di un treno ecc.).
Bibliografia
[1] DirtyDeeds, Forze elettrostatiche nei condensatori.
[2] S. D. Senturia, Microsystem Design, Springer, 2000.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)