Cos'è ElectroYou | Login Iscriviti

ElectroYou - la comunità dei professionisti del mondo elettrico

8
voti

Calcolo della capacità di un condensatore. Una applicazione del metodo dei momenti.

Indice

Introduzione

La prima parte di questa memoria presenta una breve spiegazione dei fenomeni elettrostatici e circuitali in modo da introdurre il concetto di capacita' dielettrica e condensatore.

Nella seconda parte, invece, viene presentata una spiegazione del metodo dei momenti e una sua applicazione pratica per il calcolo della capacita' di un condensatore piano.

Prima parte - Modello circuitale del condensatore

Tubi di flusso dello spostamento elettrico e condensatore

Per studiare i fenomeni dielettrici dal punto di vista circuitale e' necessario considerare l'ipotesi elettrostatica e i tubi di flusso del vettore spostamento elettrico \mathbf{D}\left ( P, t \right ). Nei mezzi dielettrici ordinari la permettivita' relativa varia nell'intervallo 1÷8 (aria-marmo), pertanto il solo fenomeno della rifrazione non e' in grado di confinare le linee vettoriali dello spostamento elettrico.

Il confinamento dei fasci del vettore D dipende in primo luogo dalla distribuzione delle cariche spaziali libere che individuano regioni delimitate dello spazio entro cui le linee di D sono canalizzate.

All'interno di queste regioni (mezzo lineare ed isotropo) e' possibile individuare porzioni di spazio in cui \triangledown \cdot \mathbf{D}\left ( P,t \right )=0, permettendo di considerare il tubo di flusso di \mathbf{D}\left ( P, t \right ). Date le condizioni elettrostatiche, il tubo di flusso non e' chiuso in quanto le linee di D nascono e muoiono in corrispondenza delle cariche libere presenti al di fuori del tubo stesso.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

All'interno del tubo di flusso e' presente anche il campo coulombiano \boldsymbol{E_{c}}.

Si definisce capacita' dielettrica del tubo di flusso di D il rapporto:

C_{AB}=\frac{\int_{S_{t}}\mathbf{D\cdot \boldsymbol{n}}\, \rm{d}S}{\int_{S_{AB}}\boldsymbol{E_{c}\cdot \boldsymbol{t}\, }\rm{d}l}=\frac{\Theta }{v_{AB}}

e si misura in farad [F].

Una struttura tipica in grado di realizzare tale situazione e' il condensatore, costituito da due conduttori, detti armature, con interposto uno o più mezzi dielettrici.

Sulle armature sono depositate le cariche elettriche libere uguali ed opposte.

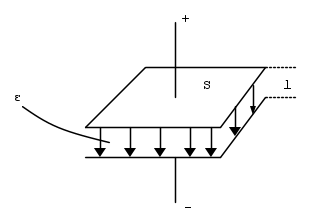
Il condensatore piano con dielettrico uniforme

E' un condensatore con elevata simmetria costituito da due armature piane e parallele di uguale superficie poste a distanza l e con interposto un mezzo dielettrico uniforme con costante dielettrica \varepsilon, come rappresentato nella figura seguente:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Trascurando gli effetti ai bordi delle armature (in pratica si considera omogenea la distribuzione delle cariche nelle due armature) la capacita' del condensatore piano vale:

C=\frac{\varepsilon S}{l} (1)

In queste condizioni ideali, i campi sono nulli esternamente alle due armature.

Il modello bipolare del condensatore

Nelle condizioni di idealità e ipotesi assunte in questa memoria, il tronco di flusso di \mathbf{D}\left ( P, t \right ) puo' essere considerato come un bipolo, caratterizzato dalla relazione q_{A}\left ( t \right )=C\, v_{AB}\left ( t \right ).
In particolare, il bipolo condensatore e' caratterizzato da una superficie chiusa al di fuori della quale lo spostamento elettrico e' nullo ovunque e in ogni istante di tempo, dalla tensione tra i terminali v_{AB}\left ( t \right ) e dalle correnti ai terminali i\left ( t \right ).

Il simbolo utilizzato in elettrotecnica per individuare il bipolo condensatore e' il seguente:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

In generale, nelle diverse applicazioni pratiche e teoriche, salvo studi di carattere specifici, il condensatore si ritiene indeformabile dal punto di vista meccanico; la deformazione della geometria del condensatore, comunque, comporta la variazione della capacita' del condensatore.

Seconda parte - Il metodo dei momenti (MoM) e il calcolo della capacita' di un condensatore piano

Il metodo dei momenti (MoM)

Il metodo dei momenti, relativamente ai problemi elettromagnetici, e' stato descritto per la prima volta da R. F. Harrington nel suo libro, ormai diventato un classico, Field Computation by Moment Methods, edito da Krieger Publishing Co., Inc. nel 1968.

E' utilizzato soprattutto per studiare la risposta elettromagnetica delle antenne o di altre strutture metalliche (radiation and scattering problems).

L'approccio generale individua il metodo dei momenti con gli operatori e gli spazi lineari, considerando la relazione:

L\left ( f \right )=g

ove:

  • f è una funzione di tipo integrale o differenziale. Nei problemi elettromagnetici rappresenta la risposta alle sollecitazioni;
  • g è il termine noto. Nei problemi elettromagnetici rappresenta l' eccitazione (tensioni, correnti o campi);
  • L e' un operatore che opera su f (f e' il dominio di L).

L'applicazione pratica di questo metodo numerico e' presentata nel prossimo paragrafo, calcolando la capacita' di un condensatore piano, costituito da due piatti conduttori paralleli di spessore trascurabile e posti a distanza d (problema bidimensionale).

Si metterà in evidenza che, quando non e' possibile trascurare gli effetti dei bordi, il valore della capacita' calcolata secondo la (1) introduce errori inaccettabili, soprattutto per applicazioni a frequenza elevata.

Il calcolo della capacita' di un condensatore piano

Come anticipato, il problema da risolvere e' il calcolo della capacita' di un condensatore piano a facce piane e parallele di lati 0,5 m \times 0,5 m posti alla distanza di 5 cm in aria. Sulla armatura superiore e' impresso un potenziale costante pari a 1 V, mentre l'armatura inferiore e' mantenuta a -1 V (d.d.p. pari a 2 V).

Lo schema bidimensionale con la discretizzazione delle armature e' presentato nella figura seguente:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Per determinare la densità superficiale di carica σ sulle armature, si divide ciascuna armatura in n sezioni (in totale si hanno 2n elementi superficiali), determinando 2n superfici ΔS elementari.

Il potenziale dell'armatura Vi al centro della generica sezione elementare vale:

V_{i}=\frac{1}{4\pi \varepsilon }\int \frac{\sigma \, \rm{d}S}{R}\approx \sum_{j=1}^{2n}\sigma _{j}A_{ij}

Il generico coefficiente Aij vale:

A_{ij}=\frac{1}{4\pi \varepsilon }\int_{\Delta S_{j}} \frac{\, \rm{d}S_{j}}{R_{ij}} (2).

In forma matriciale il problema si scrive:

\boldsymbol{A\sigma }=\boldsymbol{v},

da cui si ottiene:

\boldsymbol{\sigma }=\boldsymbol{A}^{-1}\, \boldsymbol{v}

costituendo un sistema di 2n equazioni in 2n incognite σ. Il vettore v e' il vettore dei potenziali (i primi n elementi sono pari a V1 e i restanti pari a V2), A e' la matrice dei coefficienti di auto e mutua influenza 2n\times 2n simmetrica, i cui elementi sono stati definiti in (2).

Le distanze Rij fra i baricentri delle singole celle elementari della sezione sorgente e della sezione osservazione valgono:

R_{ij}=\sqrt{\left ( x_{j}-x_{i} \right )^{2}+\left ( y_{j}-y_{i} \right )^{2}+\left ( z_{j}-z_{i} \right )^{2}}

calcolate sulla base della figura seguente:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

I coefficienti Aij di mutua e auto influenza valgono:

A_{ij}=\left\{\begin{matrix} \frac{\Delta l^{2}}{4\pi \varepsilon R_{ij}}\; per \; i\neq j\\ \\ \frac{\Delta l\; \ln \left ( 1+\sqrt{2} \right )}{\pi \varepsilon}\; per\; i=j \end{matrix}\right.

assumendo quadrata ciascuna sezione elementare, di lato pari a Δl.

Implementazione e risultato

L'algoritmo presentato e' stato implementato in linguaggio Python (interprete Python 3.6.5), utilizzando le librerie esterne NumPy e Matplotlib.

Con i dati riportati all'inizio di questa seconda parte e suddividendo ogni singola armatura in 400 celle quadrate elementari, l'algoritmo restituisce un valore di capacita' pari a

C=\frac{Q}{\left | V_{1} -V_{2}\right |}=58{,}12\; \rm{pF}

La carica Q e' calcolata sommando i primi n elementi del vettore \boldsymbol{\sigma } (prima armatura) e moltiplicando il valore ottenuto per l'area di una singola cella elementare.

Le figure seguenti mostrano le densità di carica sull'armatura superiore e inferiore:

figura1.png

figura1.png

figura2.png

figura2.png


Calcolando la capacita' dello stesso condensatore secondo la relazione (1) si ottiene:

C=\frac{\varepsilon S}{d}=\frac{8,8541\times 10^{-12}\times 0,25}{0,05}=44,27\; \rm{pF}

Conclusioni

Il risultato deve far riflettere soprattutto gli studenti alle prime armi. Prima di applicare una formula e' necessario chiedersi se le relative ipotesi siano soddisfatte, poiché il risultato ottenuto, in caso contrario, e' errato.

E' necessario, dunque, analizzare il problema con senso critico prima di affrontarlo numericamente.

Bibliografia

  1. Massimo Guarnieri, Gaetano Malesani: Elementi di elettrotecnica - Elettromagnetismo stazionario e quasi-stazionario, Edizioni Progetto Padova, 1999.
  2. Alberto Gigli Berzolari: Introduzione all'elettromagnetismo, seconda edizione, la goliardica pavese, 1973.
  3. Cesare Mario Arturi: Campi elettrici, magnetici e di conduzione - Introduzione ai metodi computazionali, Maggioli editore, 2008.
  4. Valeriano Comincioli: Analisi numerica - Metodi modelli applicazioni, McGraw-Hill, 1995.
  5. Walton C. Gibson: The Method of Moments in Electromagnetics, Chapman and Hall/CRC, 2008.
  6. The Method of Moments in Electromagnetics, Massachusetts Institute of Technology, 6.635 lecture notes.
  7. Travis E. Oliphant: Guide to NumPy, 2006
  8. NumPy Reference 1.15, 2018.
  9. Matplotlib User's Guide 2.2.3, 2018.
Estratto da "https://www.electroyou.it/mediawiki/index.php?title=UsersPages:Edmonddantes:calcolo-della-capacit-di-un-condensatore-una-applicazione-del-metodo-dei-momenti"
6

Commenti e note

Inserisci un commento

di ,

Chiarissimo, ora mi torna! L'argomento è sicuramente molto ampio, però come assaggio non è per niente male!

Rispondi

di ,

Ciao, ti ringrazio per l'intervento. Mi fa piacere che qualcuno legga con interesse i miei lavori. Per quanto riguarda densità di carica hai ragione, ho la cattiva abitudine di modificare le formule già scritte. Si tratta di refuso, infatti, avrai notato che le Aij scritte dopo non hanno quel termine. Lo modificherò a breve. Ancora grazie. I risultati numerici e grafici sono corretti, in quanto ho fatto diverse prove su esempi noti. Per quanto riguarda la distanza zj-zi, invece, non e' possibile inserire d, in quanto non saresti in grado di valutare i coefficienti di autoinduzione o di mutua induzione fra elementi appartenenti alla stessa armatura (quella distanza zj-zi varia assume valori pari a 0, d, e -d). Inoltre, hai anche il vantaggio di avere un vettore z utile per fare qualche prova extra. Riconosco che l'articolo e' breve, ma la dimostrazione completa di tutti i passaggi richiede almeno un paio di pagine A4. Il mio intento e' quello di far comprendere che non bisogna risolvere i problemi applicando le formule a "memoria". Ovviamente questo non vale per te... hai visto quel refuso individuabile solo se ti metti a fare i passaggi. Per ottenere quei risultati e' necessario eseguire qualche integrale, di cui uno doppio, e per quanto riguarda il coefficiente di autoinduzione ipotizzare una carica uniformemente distribuita su tutta la superficie dell'elemento DS.

Rispondi

di ,

Buongiorno, l'articolo è molto interessante, complimenti! Volevo chiederti due chiarimenti riguardo le relazioni usate nell'articolo: nell'espressione (2) del coefficiente Aij non dovrebbe non esserci la densità di carica superficiale sigma? Senza la densità di carica superficiale sigma, la dimensione di Aij sarebbe quella di una superficie fratto la capacità, invece con la densità di carica superficiale Aij è già una tensione. Poi, nell'espressione per la distanza Rij, (zj-zi)^2 può essere sostituito direttamente da d^2 poiché la distanza fra le due armature è costante, giusto? Detto questo, nel calcolo di Aij con i=j otterrei: ((delta l)^2)/(4*pi*epsilon*d), diversamente da quanto scritto nell'articolo. Volevo chiederti quindi in che modo hai ottenuto tale risultato e devo posso aver sbagliato.

Rispondi

di ,

Grazie RenzoDF, ho qualcosa nel mio cassetto. Simulazione FDTD, un modello di un motore asincrono implementato in Python e altra robetta simile.

Rispondi

di ,

Davvero un bell'articolo Edmond, sarebbe interessante accennare al confronto con gli altri metodi di analisi numerica, per esempio con FEM o FDTD.

Rispondi

Inserisci un commento

Per inserire commenti è necessario iscriversi ad ElectroYou. Se sei già iscritto, effettua il login.