
Pietro
Moderatori: ![]() PietroBaima,
PietroBaima, ![]() Ianero
Ianero




 e verso
e verso  .
.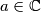


PietroBaima ha scritto:really easy piece.




PietroBaima ha scritto:la sequenza di operazioni fatta svolgere al programma.
PietroBaima ha scritto:Attento.

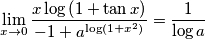
 se
se 
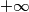 se
se 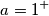
 se
se 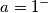
dipende dal condizionamento del problema


Visitano il forum: Nessuno e 4 ospiti