La teoria matematica per il calcolo di aree di superfici nello spazio tridimensionale comporta l'uso di integrali quasi sempre di difficile soluzione. Scopo di questo articolo è l'approccio a questi problemi con metodi elementari, sfruttando velocità e precisione dei PC, mediante l'impiego delle differenze finite.

Superfici piane nello spazio tridimensionale

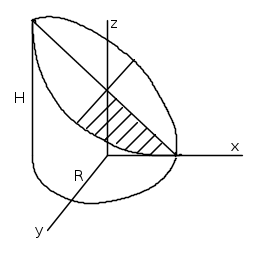
Iniziamo da un semplice esempio di calcolo della sezione obliqua di un cilindro attorno all'asse z e di altezza H, con base di raggio R sul piano x-y.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

L'esempio è abbastanza banale e non occorrono integrazioni per risolverlo, ma è utile per capire l'applicazione del metodo delle differenze finite e controllarne la precisione.
Si vede infatti che la sezione obliqua è un'ellisse di semiassi e , quindi l'area As non è altro che il prodotto dei semiassi per π.
Anche l'area laterale Al del semicilindro non è altro che la metà di quella del cilindro.

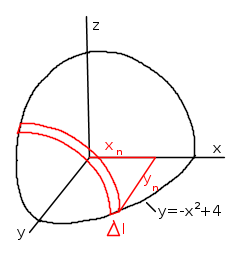
Applicheremo le differenze finite ad un quarto di sezione (quella tratteggiata nella figura), suddividendo in N incrementi z_n il tratto H/2 e ricavando poi l' x_n corrispondente che interseca il piano della sezione. Con questi dati possiamo ricavare y_n che corrisponde al punto (P) del'ellisse, cioè dell'intersezione del piano con il cilindro.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Per ricavare la superficie, la coordinata y_n deve essere moltiplicata per la la larghezza Δl, cioè per la striscia di piano che corrisponde agli incrementi stabiliti per z e x. Questo valore è costante dato che la figura è appunto piana.
Ed ecco lo svolgimento con Mathcad Express:

Ovviamente variando N varia la precisione del risultato delle differenze finite ed è interessante, una volta impostata la procedura di calcolo, variare i dati di partenza: l'aggiornamento delle soluzioni avviene in pochi secondi.

Superfici di rotazione

Le più comuni forme di superfici tridimensionali sono quelle generate dalla rotazione di una curva attorno ad un asse. Conoscendo l'equazione della curva, è possibile calcolarne l'area fra dati limiti.
Prendiamo come esempio la parabola vista per la rettificazione. Facendo ruotare la parabola attorno all'asse y, si ottiene un paraboloide:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

La figura mostra un quarto di elissoide ed illustra l'applicazione delle differenze finite: si genera la serie di x_n fra i limiti, si calcola il corrispondente y_n, quindi il Δl_n e lo si moltiplica per il percorso di rotazione di questo (cioè ). Δl è il tratto elementare di curva già visto nella rettificazione.
Ecco lo svolgimento in Mathcad Express:

Per il confronto con la normale prassi d'integrazione si noti che, passando agli infinitesimi, risulta:

quindi si deve integrare fra i limiti di x(0;2) il prodotto del raggio di rotazione (x_n) e dl.

Un'altra possibile procedura di confronto è data dalla regola di Guldino. Questa stabilisce infatti che l'area della superficie di rotazione di una data curva è esprimibile con il prodotto della lunghezza della curva () ed il percorso rotatorio del suo baricentro ().

Superfici algebriche

Altro interessante tipo di superficie tridimensionale è quello della forma z = f(x,y)
In questo caso i limiti sono dati dalla proiezione della superficie sul piano x-y per z=0
Anche in questo caso, esamineremo una superficie piana per meglio capire il metodo adottato.

(la figura è ottenuta con Mathcad tradizionale, poiché l'edizione gratuita Express non permette grafici tridimensionali).

Imponendo il passaggio in tre punti, ad es. le coordinate di A(2,0,1),B(0,0,2) e C(0,3,1), si ottiene l'equazione del piano:

La figura ottenuta non è un rettangolo (gli angoli non sono di 90°), ma può essere approssimato ad un rettangolo con un piccolo errore (in questo caso dell'1%).In realtà bisognerebbe fare il prodotto vettoriale, ad es. e la teoria conduce alla soluzione di


dove f è appunto la z = f(x,y)
Nel nostro caso diventa:

Approssimandolo ad un rettangolo, possiamo ricavare i lati


Il loro prodotto è

Questo si mantiene anche se suddividiamo la figura in tanti "rettangolini", ognuno corrispondente alla proiezione sul piano x-y per z=0. Questa proiezione può essere vista come incrementi Δx e Δy stabiliti.
In definitiva , il metodo delle differenze finite, richiede la suddivisone dei limiti in incrementi (N in x,M in y), il calcolo degli z_n,m valori della funzione, il calcolo dell'area di ciascun "rettangolino" della superficie, ed infine la somma di queste aree. Ecco il calcolo in Mathcad Express dell'area della porzione di piano considerata:

Come si vede, dà la stessa approssimazione del calcolo precedente.

Un esempio

Come esempio di applicazione, supponiamo di dover determinare l'area della superficie curva espressa da:
nei limiti e
La funzione può essere rappresentata in Mathcad (non Express), sia come sia prospetticamente che a curve di livello:

Il calcolo in Mathcad Express é:

L'errore in questo caso è del 2%, ma si noti che il procedimento ha il vantaggio di usare la stessa formula, quindi lo stesso programma di calcolo, per superfici diverse (ovviamente cambiando i limiti e l'espressione della funzione), mentre per la soluzione matematica, occorre risolvere l'integrale di volta in volta.
Va infine notato che il metodo consente anche calcoli su NxM dati,sotto forma di z_n,m, non necessariamente legati a funzioni matematiche (come ad es. dati raccolti sperimentalmente).

Nota aggiuntiva al calcolo di superfici algebriche

Si è detto che con la suddivisione della superficie in “rettangolini”, il calcolo delle singole aree può essere ottenuto approssimandolo con un prodotto scalare dei lati, anziché con il loro prodotto vettoriale.
Questo comporta un errore che cresce con la pendenza della superficie, quindi trascurabile se la pendenza non è elevata (diciamo entro i 45°).
Sfruttando le possibilità di Mathcad Express di svolgere anche prodotti vettoriali, si può superare questa approssimazione con una procedura che ricavi i lati come vettori. Il metodo è quindi concettualmentepiù complicato, ma elimina gli errori dovuti alla deformazione del “rettangolino” elementare.
In pratica i lati di ciascun “rettangolino” sono definiti dai vettori vx e vy, con i quali si ricava la singola area Δa corrispondente, come modulo del loro prodotto vettoriale.
Per ottenere il valore della superficie entro i limiti stabiliti, non resta quindi che sommare gli NxM valori di Δa.

Ecco dunque la procedura alternativa applicata all’esempio precedente.

Come si vede, in questo caso di piccole pendenze, il risultato addirittura coincide con quello “teorico”.