Una delle maggiori limitazioni della versione gratuita Mathcad Express rispetto al Mathcad originale o al nuovo Prime2 è l'impossibilità di ottenere rappresentazioni tridimensionali di funzioni matematiche.
Questo articolo mostra come sia possibile utilizzare Express per superare questa limitazione.
Indice |
La rappresentazione assonometrica
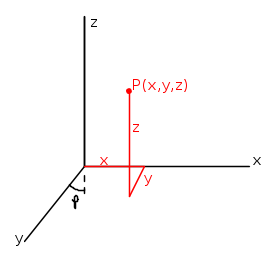
Com'è noto, un punto nello spazio tridimensionale è definito da tre coordinate (x,y,z), ma se si vuole rappresentarlo su un piano occorre ridurlo a 2 coordinate, mettendo uno degli assi (y) inclinato di un angolo (φ) rispetto alla verticale (z). E' questa la rappresentazione nota come assonometrica, illustrata nella seguente figura:
La posizione di un generico punto sul piano del disegno (XZ) è allora determinata dalle due coordinate x e z, "corrette" per tener conto della terza (y), cioè  .
.
I valori più usati per  sono 30° e 45°, a cui corrispndono i coefficienti moltiplicatori di y
sono 30° e 45°, a cui corrispndono i coefficienti moltiplicatori di y 
 e rispettivamente
e rispettivamente 

Segmento fra due punti
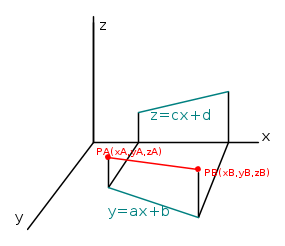
Dati allora due punti PA(xA,yA,zA) e PB(xB,yB,zB) è possibile rappresentare il segmento di retta che li unisce calcolando i parametri delle due che ne rappresentano la proiezione rispettivamente sul piano xy e xz.
La traccia rossa rappresenta il segmento, quelle blu le proiezioni con le rispettive espressioni.
Ecco la procedura in Mathcad Express:
Con la matrice H si hanno i riferimenti alle coordinate dei due punti per il calcolo dei coefficienti delle proiezioni, dopodiché si scrivono le espressioni delle rette corrispondenti per ottenere infine i valori di X e Z per la rappresentazione assonometrica, che risulta questa:
Si noti che il metodo vale per  , altrimenti bisogna scegliere un'altra coordinata
come variabile indipendente.
, altrimenti bisogna scegliere un'altra coordinata
come variabile indipendente.
Rappresentazione di superfici
E' abbastanza evidente che se si possono rappresentare punti, si possono anche rappresentare linee in tre dimensioni di qualsiasi forma. Questo permette anche di definire delle superfici tridimensionali, tracciando una serie di curve che ne rappresentino sezioni.
Consideriamo una sfera unitaria, cioè di equazione x2 + y2 + z2 = 1,e rappresentiamone la sezione che ha per base il piano xy ed è delimitata a  .
.
Il procedimento in Mathcad express è il seguente:
Si suddividono i tratti x e y rispettivamente in N ed M parti e si calcola il valore di z in ciascuno.
Si ricavano infine le coordinate di X e Z per la rappresentazione assonometrica.
Il tracciamento delle singole sezioni è ottenuto dagli indici dati a queste matrici di dati (ovviamente per ogni curva con i medesimi indici di Z e di X). Ed ecco il risultato col tracciamento delle sezioni estreme:
Cambiando i limiti di x e y (da 0 a 1) ed i riferimenti delle varie curve, con lo stesso programma si può ottenere la rappresentazione di 1/8 di sfera:
Se invece di x e y , scegliamo x e z come variabili indipendenti, quindi ricaviamo y con il calcolo della funzione y = f(x,z), con lo stesso impianto di calcolo ricaviamo figure come questa:
Questo approccio consente di passare ad un'altra ben nota forma di rappresentazione tridimensionale: le curve di livello. Fissando infatti il valore di z e variando x, si ricava dall'espressione della superficie il valore esplicitato di y corrispondente a ciascun valore di x.
Curve di livello
Ecco infatti la procedura in Mathcad Express per questo tipo di rappresentazione. L'esempio si riferisce ad una superficie del tipo chiamato "a sella", con espressione  .
.
Come si vede, fissati gli intervalli di x e z, viene calcolata la matrice yn,m che permette di ottenere le singole curve di y in funzione di z (fissato) e x, nel suo intervallo stabilito.
Nel grafico vengono tracciate le curve  , ecc.,
corrispondenti rispettivamente a z=-0.1, -0.05, 0, 0.05, 0.1 e 0.15.
, ecc.,
corrispondenti rispettivamente a z=-0.1, -0.05, 0, 0.05, 0.1 e 0.15.
Conclusioni
Le procedure illustrate non hanno la pretesa di rivaleggiare con le più sofisticate prestazioni dei software di grafici 3D del Mathcad originale o del nuovo Prime2, ma rappresentano una possibilità di utilizzo dell'edizione gratuita Mathcad Express per lo studio di funzioni tridimensionali.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)