Introduzione
Salve a Tutti! Allora, come si evince dal titolo, si parlerà dei tanto discussi Impianti Nucleari usati per la produzione di Energia Elettrica. Sarà un percorso a più articoli e vedremo inanzi tutto gli aspetti generali della Fisica Nucleare e poi la componentistica e tipologie di Reattori presenti negli Impianti Nucleari di Potenza, meglio conosciuti anche come Impianti Elettronucleari. Non si può prescindere dalla storia e dalle "Rivoluzioni" che, ahimè, gli ERRORI UMANI (E SOLO QUELLI!!!), hanno apportato agli impianti ed alla Fisica delle Reazioni Nucleari. L'indice è il seguente:
- Fisica delle Reazioni Nucleari (solo un accenno)
- Tipologie di Reattori Nucleari (seguendone l'evoluzione)
- Impianti Nucleari
- Il contesto energetico
- Conclusioni (con dati e meno politica)
Fisica delle Reazioni Nucleari
Il nucleo e’ costituito da nucleoni, protoni di carica positiva e neutroni neutri. La massa dei nucleoni e’ approssimativamente la stessa: Mp = 1.67239 x 10-24[g], Mn = 1.67470 x 10-24[g]. Nuclei aventi lo stesso numero di protoni Z sono chiamati isotopi, mentre quelli con lo stesso numero di massa sono detti isobari. La massa in fisica nucleare e’ misurata, analogamente a quella atomica, in unita’ di massa atomica [amu], definita come 1/12 della massa del C12, uno degli isotopi del Carbonio, che equivale a 1.6582x10-24[g] o 931.44 [MeV].
Mass defect
La differenza di massa ΔM tra la massa del nucleo in amu, ed il suo numero di massa A e’ chiamata mass defect del nucleo:
Atomic Mass Unit = 1/16 massa del O16 cioè la sedicesima parte della massa di Ossigeno 16.
1amu = 1,66 *10-24[g] :
- Mn = 1,00897 [amu]
- Mp = 1,00758 [amu]
- Me = 0,000549 [amu]

- Mz,a = massa del nucleo in esame
- Mp = massa del protone
- Mn = massa del neutrone
- z = numero atomico
- a = numero di massa
Ebbene sì, il nucleo formato da n "palline", pesa MENO della somma delle palline singole! Bisognerebbe inoltrarci nella Fisica "Pesante".. ma, agli Ingegneri, o gli "Energetici" come me, bando alle ciance, qui c'è ENERGIA!.
Dov'è finita la massa??? scomparsa?? Impossibile. Forse nascosta.. mah.. La risposta è , si è trasformata; e in che cosa? Ce lo dice Einstein:
E = Mc2
Il difetto di massa, è l'ammontare energetico RILASCIATO dai nucleoni (neutroni e protoni) per stare attaccati!
In sostanza: se voi avete i nucleoni sparsi a distanza e volete riattaccarli formando un nucleo, questi vi rilasciano energia, mentre se li dividete dovete fornire energia. Ci sarebbero molti e molti dettagli e precisioni da fare, ma il campo Fisico delle reazioni e un campo pieno di insidie e specialistico. Quando condussi gli studi universitari sugli impianti nucleari, essendo ad Ingegneria si ometteva spesso e allo studio, e all'esame, la parte di Fisica, se non per quanto riguarda la base di come capire da dove viene questa energia. L'importante, a mio avviso, è sapere che per formarsi il nucleo rilascia di energia, per separare i nucleoni l'uno dall'altro occorre fornire energia. L’energia di legame (BE) di un nucleo rappresenta il lavoro richiesto per separare il nucleo nei suoi nucleoni costituenti, oppure come l’energia rilasciata durante la formazione del nucleo dai suoi costituenti.
Ma il livello di Binding Energy, non è uguale per tutti gli atomi della tavola periodica, ma ha un andamento a massimo come illustrato in figura; in realtà è meglio diagrammare, non tanto la Binding Energy, ma la Binding Energy specifica, ossia per nucleone
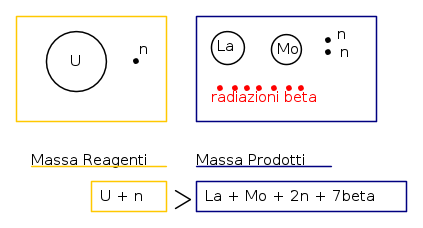
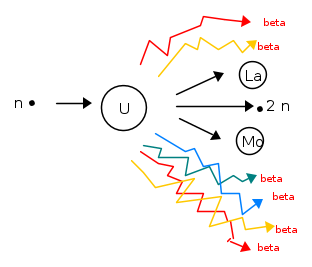
ATTENZIONE: il quantitativo di BE (Binding Energy) nell'Uranio, è decisamente superiore a quella del Ferro; semplicemente perchè l'Uranio ha più nucleoni; ma la BE per nucleone è minore. Ossia, quando si è formato il nucleo di Ferro, esso ci ha rilasciato un quantitativo di Energia minore di quello che ci ha lasciato il nucleo di Uranio, ma rispetto al numero di nucleoni cui esso è composto, di più, rispetto all'Uranio. La BE/nucleon (Binding Energy per nucleon), è maggior nel Ferro che nell'Uranio (in quest'ultimo la BE/nucleon è talmente bassa che qualche nucleone tende a scappare... questo è alla base del fenomeno delle emissioni di radiazioni). Quindi se io divido il nucleo di Uranio a formare altri due nuclei più piccoli a più alta BE/n, allora, visto che il numero di particelle, protoni e neutroni, rimane costante(!!), i due frammenti rilasceranno Energia. Vediamo un esempio:
92U235+0n1 → 42Mo95+57La139+20n1+7 -1β0
Che presenta una variazione di massa tra prodotti e reagenti di:(m92U235 = massa dell'Uranio 235.. e così via)
Δm =m92U235+m0n1-m42Mo95-m57 La139-2m0n1 =0,22283 [amu] = 0,3699*10-24[g]
Rappresenta "graficamente" una delle miliardi di possibili reazioni di fissione dove si producono CASUALMETE Lantanido (La) e Molibdeno (Mo)
che origina una energia pari a: Δm*c²= 207,45 [MeV] che diventa 191[MeV] eseguendone la media tra le tipologie di reazione che avvengono e tenendo conto dell’energia che hanno ineutroni prodotti.
La tecnologia prevede il bombardamento di un nucleo con un neutrone di una certa energia sufficiente ad ottenere la formazione di due prodotti di fissione energeticamente stabili e in piú dei neutroni aggiuntivi addetti alle successive fissioni. Il comportamento dei nuclei del fascio neutronico è molto entropico e casuale, e possono essere:
- assorbiti dai nuclei;
- rimbalzati dai nuclei;
- fissare i nuclei;
Tutte queste possibilità hanno una loro probabilità di avverarsi, a seconda della composizione chimica del combustibile nel suo lento esaurimento, essendo composto sempre piú di atomi non fissibili. Gli atomi a nucleo fissibile sono essenzialmente tre:
- 92U235
- 92U233
- 94Pu239 ;
gli ultimi due non esistono in natura ma sono presenti nei reattori nucleari secondo le reazioni di formazione:
- Uranio 233: 90Th232+0n1→90Th233 → 90Th233 → 91Pa233+-1β0(T=23.5 minuti spontanea) → 92U233+-1β0(T=27.4 giornispontanea)
- Plutonio 239: 92U238+0n1→92U239 → 93Np239+-1β0(T=2.35 minuti spontanea)93Np239 → 94Pu239+-1β0(T=2.3 giorni spontanea)
Burn-Up I: è la media Energia liberata da una fissione nucleare
1 grammo di U235 contiene Navogadro/235 nuclei; se tutti venissero fissionati, si otterrebbe un’energia specifica di :
191⋅N/235 [MeV/grammo U-235] = I = 0.9 [MWd/grammo U-235] pari a I=900.000 [MWd/ton U-235]
- 1[MeV]= Mega elettronVolt, unità di misura dell'ENERGIA: 1 eV = 0.160217653 [aJ]
- 1[MWd]( MegaWattDay) = 24000[KWh] x 860 = 2*10⁷ [Kcal] = 2 [toe]
Siccome lavoriamo con Uranio o naturale o arricchito(enriched), otteniamo:
- uranio naturale (0.7% di fissile) I = 900000⋅0.7/100 = 6300 [MWd/ton]
- uranio arricchito (3% di fissile) I = 900000⋅3/100 = 27000 [MWd/ton]
. I = 27000 [MWd/tenrich] = 54000 [toe/tenrich] = 10000 [toe/ton_nat]
. tonenrich = 5,4 tonnat (per produrre una tonnellata di Uranio al 3% servono 5,4 di naturale)
Quello che salta all'occhio è il quantitativo di ENERGIA presente in una tonnellata di Uranio enriched: 648.000.000 [kWh/ton];
l'Energia prodotta d 648.000.000 x 10 = 6 miliardi e mezzo di pannelli FV da 100 [W] picco, funzionanti per 1 h alla potenza costante di 0,1[kW] ciascuno
- per 10 perchè ipotizzo pannelli da 100 [Wpicco] comuni
- 648.000.000 = 27.000 [MWd/tenrich] * 24000[KWh]
Non tutte le reazioni sono come quella illustrata, ho voluto mettere la classica dei libri di testo.
L'andamento % dei prodotti è in questa foto seguente, dove, un'ulteriore discriminante è l'energia del neutrone che "bombarda".
Questa è una delle ROGNE peggiori nella costruzione di un reattore. BISOGNA FRENARE I NEUTRONI FINO AL LIVELLO CONSONO A FISSARE UN ALTRO NUCLEO. Questo è un punto importantissimo! e lo vedremo nel prossimo articolo. Vi elenco solo le tipologie di Reattori che metterò nei prossimi articoli:
- Magnox
- AGR (Advanced Gas Reactor)
- HTGR (High Temperature Gas Reactor)
- BWR (Boiling Water Reactor)
- PWR (Pressurized Water Reactor)
- Candu (Canadian Deuterium Reactor)
- RBMK (Chernobyl)
- AP1000
- FBR (Fast Breeder Reactor)
- Il "nostro" EPR

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)