Indice |
INTRODUZIONE
Ho notato che spesso nel forum ricorrono domande sull'utilizzo dei wattmetri, soprattutto nei sistemi trifase e che a volte non è ben chiaro cosa misura tale strumento. Poiché io ho le idee tutt'altro che chiare, giusto per confondere ancor di più il mal capitato che si trovasse a leggere queste inutili note, scriverò dell'uso di codesto strumento per come l'ho sempre (male) utilizzato...
IL SEMPLICE CASO DELLA CORRENTE CONTINUA
La potenza elettrica in corrente continua è : quindi basta misurare la tensione e la corrente e moltiplicarle ed il gioco è fatto.
E che c'entra inventare un nuovo strumento se gia voltmetro e amperometro l'hanno già inventati? Certamente per evitare di fare la moltiplicazione. Pensate sia semplice moltiplicare? L'avete mai fatto con i numeri con la virgola? E non venite a dirmi che hanno inventato le calcolatrici...
Il wattmetro è stato inventato per non eseguire operazioni aritmetiche, infatti, con lo stesso strumento si misurano contemporaneamente la tensione e la corrente e "gualà" la potenza è bella e misurata, in watt naturalmente, altrimenti, se avesse misurato i cavalli vapore, lo strumento si sarebbe chiamato "cavallovaporemetro" che poi sarebbe stato uno strumento approssimativo perchè non sarebbe stato in grado di distinguere gli "asini fumo" (sottomultiplo dei cavalli vapore)...
quindi basta misurare la tensione e la corrente e moltiplicarle ed il gioco è fatto.
E che c'entra inventare un nuovo strumento se gia voltmetro e amperometro l'hanno già inventati? Certamente per evitare di fare la moltiplicazione. Pensate sia semplice moltiplicare? L'avete mai fatto con i numeri con la virgola? E non venite a dirmi che hanno inventato le calcolatrici...
Il wattmetro è stato inventato per non eseguire operazioni aritmetiche, infatti, con lo stesso strumento si misurano contemporaneamente la tensione e la corrente e "gualà" la potenza è bella e misurata, in watt naturalmente, altrimenti, se avesse misurato i cavalli vapore, lo strumento si sarebbe chiamato "cavallovaporemetro" che poi sarebbe stato uno strumento approssimativo perchè non sarebbe stato in grado di distinguere gli "asini fumo" (sottomultiplo dei cavalli vapore)...
Si ma il wattmetro che tensione e che corrente misura?
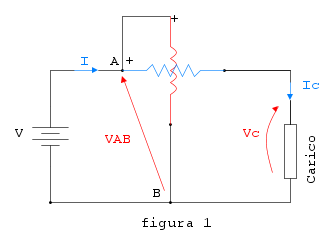
Se sapevessi... sapevavo... saputavo... ah ecco! Se sapessi ripsondere a questa domanda non ero quì a scriverne ero da qualche parte ad usarlo. Comunque... Il wattmetro, una volta collegato in un circuito (figura 1),
misurerà il prodotto fra la tensione VAB a cui è sottoposto il circuito voltmetrico (quello rosso), e la corrente I che attraversa il circuito amperometrico (quello celeste). Trascurando le perturbazioni (minime) introdotte dallo strumento, la tensione e la corrente suddette altro non sono che la tensione Vc e la corrente Ic afferenti al carico, quindi il wattmetro misurerà la potenza elettrica di tale carico, cioè 
Quindi?
Quindi non importa a quale tensione sarà sottoposta il circuito voltmetrico e quale corrente attraverserà quello amperometrico, il wattmetro indicherà sempre il prodotto fra queste due grandezze.
COSA CAMBIA IN REGIME SINUSOIDALE (corrente alternata)
IL nostro strumento in regime sinusoidale misura la potenza. Si bella scoperta anche in regime stazionario (corrente continua) lo faceva, allora cosa c'è di diverso? Nulla o forse tutto. È noto ai più (non a me ovviamente!) che in regime sinusoidale vi sono tre potenze:
- Potenza Attiva P, misurata in watt (W);
- Potenza Reattiva Q, misurata in volt-ampere reattivi (VAR... ehm... eh eh!... var);
- Potenza Apparente S (o A) misurata in volt-ampere (VA).
Si ribadisce che se il wattmetro si chiama wattmetro è perché misura i watt e quindi misurerà una potenza attiva.
È altresì noto che:  con V il modulo della tensione ai capi (per esempio) di una impedenza, I il modulo della corrente che l'attraversa,
con V il modulo della tensione ai capi (per esempio) di una impedenza, I il modulo della corrente che l'attraversa,  l'angolo di sfasamento fra i vettori complessi che rappresentano le dette grandezze. Pertanto nel caso di figura 3 il wattmetro darà una indicazione pari al prodotto
l'angolo di sfasamento fra i vettori complessi che rappresentano le dette grandezze. Pertanto nel caso di figura 3 il wattmetro darà una indicazione pari al prodotto  .
.
E se qualcuno (io) fa qualche collegamento strambo come in figura 4 cosa indicherà lo strumento?
Con riferimento al diagramma vettoriale su riportato lo strumento indicherà il valore relativo a

(ovviamente in watt) dove, questa volta, l'angolo  rappresenta l'angolo di sfasamento fra i vettori complessi
rappresenta l'angolo di sfasamento fra i vettori complessi  e
e  Il fatto che questa misura possa o non possa essere significativa è un altro discorso.
Il fatto che questa misura possa o non possa essere significativa è un altro discorso.
E VENIAMO AI SISTEMI TRIFASE
Che sarebbe pure ora visto il titolo....
Esaminiamo ora il sistema trifase di figura 5 (che poi perché mai scriverò al plurale se sono da solo che scrivo?). Esso è alimentato da tre generatori collegati a stella aventi stessa frequenza, fem con lo stesso valore efficace ma sfasate fra loro di 120°. Il carico è invece composto da tre impedenze uguali in modulo e in fase collegate anche loro a stella.
Ne consegue anche il diagramma vettoriale a fianco riportato, dove le tensioni  ,
,  ,
,  sono le cosiddette tensioni stellate, quelle tra una fase e i centro-stella, mentre
sono le cosiddette tensioni stellate, quelle tra una fase e i centro-stella, mentre  ,
,  ,
,  sono le cosiddette tensioni concatenate quella tra due fasi, inoltre i vettori
sono le cosiddette tensioni concatenate quella tra due fasi, inoltre i vettori  ,
,  ,
,  sono le correnti circolanti nel carico (una per fase) detto, se non sbaglio (il che nel mio caso è sempre falso) correnti di linea.
Si tratta, dunque, di un sistema trifase con un carico equilibrato alimentato da un sistema simmetrico.
Che poi è il più facile da studiare fra i sistemi trifase e chi non crede a ciò chieda pure agli studenti che studiano elettrotecnica.
sono le correnti circolanti nel carico (una per fase) detto, se non sbaglio (il che nel mio caso è sempre falso) correnti di linea.
Si tratta, dunque, di un sistema trifase con un carico equilibrato alimentato da un sistema simmetrico.
Che poi è il più facile da studiare fra i sistemi trifase e chi non crede a ciò chieda pure agli studenti che studiano elettrotecnica.
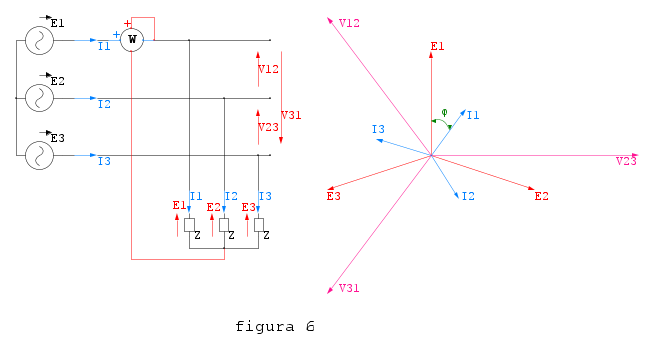
Che cosa misura il wattmetro di figura 6?
Perché mi faccio una domanda se poi devo darmi una risposta? non sarebbe meglio dare direttamente la risposta? (altre domande a me stesso, forse è il caso di chiamare gli uomini con la camicia di forza...)
Il wattmetro misura la seguente potenza:

Poiché il circuito voltmetrico è sottoposto alla fem  ,il cui modulo è E1, e quello amperometrico è attraversato dalla corrente
,il cui modulo è E1, e quello amperometrico è attraversato dalla corrente  , il cui modulo è I1 ed ovviamante l'angolo di sfasamento dra queste due grandezze è
, il cui modulo è I1 ed ovviamante l'angolo di sfasamento dra queste due grandezze è  , come da diagramma vettoriale.
, come da diagramma vettoriale.
Invece il wattmetro collegato come in figura 7 misura:
(questa volta do solo la risposta)

dove  è il modulo della tensione
è il modulo della tensione  ,
,  è il modulo della corrente
è il modulo della corrente  ed infine l'angolo
ed infine l'angolo  è l'angolo fra i vettori complessi
è l'angolo fra i vettori complessi  e
e 
Quando collego il wattmetro come in figura 8, invece
In tal caso la misura data dallo strumento sarà:

Dove  è ovviamente pari a
è ovviamente pari a  visto il collegamanto del wattmetro,
visto il collegamanto del wattmetro,  e
e  è ovviamente l'angolo tra i vettori
è ovviamente l'angolo tra i vettori  e
e  .
.
É chiaro che nella relazione che esprime la potenza compaiono i moduli dei vettori suddetti.
Conclusione
Perché mai i wattmetri, nei sistemi trifase debbano essere collegati in questa varietà di modi? (E ci risiamo con le domande auto-poste, uomini con la camicia di forza, dove siete?) Non so rispondere alla domanda, se avessi saputo farlo non avrei posto il quesito. Però posso dire che:
- il wattmetro misura solo potenze attive;
- la potenza attiva misurata è il prodotto fra il modulo della tensione applicata il circuito voltmetrico dello strumento per il modulo della corrente che attraversa il circuito amperometrico per il coseno dell'angolo tra il vettore tensione e il vettore corrente;
- se qualcuno ha inventato tale strumento di misura a qualcosa servirà;
- ovviamente i moduli delle grandezze rappresentano il valore efficace delle grandezze stesse;
- non ho mai capito perchè il wattmetro (così come gli altri stumenti funzionanti in corrente alternata) misurino il valore efficace delle grandezze;
e, soprattutto
- Non ho la più pallida idea di cosa io stia scrivendo...
APPENDICI
L'attento lettore (ammettendo che queste note lo meritino un lettore) avrà notato che qualche rigo fa ho scritto "Conclusione" ebbene ho mentito, la conclusione non concludeva affatto.
Con queste appendici mi riprometto di esaminare alcuni casi di effettivo uso dei wattmetri nei sistemi trifase per misurare qualche potenza, senza però addentrarmi nelle dimostrazioni matematiche poiché in questa "branchia" (si dirà così) della conoscenza umana sono ancor meno ferrato che nell'elettrotecnica della quale ho la pretesa di scrivere.
Appendice 1: TRE WATTMETRI
Se il sistema trifase è alimentatto da terna simmetrica che il carico sia equilibrato, sistema a tre fili (solo le tre fasi), o squilibrato, sistema a quattro fili (c'è il neutro), la misura di potenza attiva è assicurata se si utilizzano tre wattmetri.
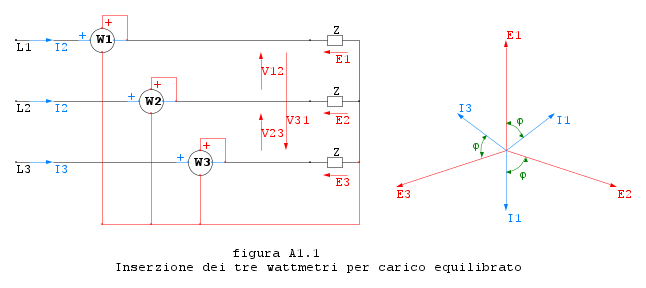
Nel caso di sistema a tre fili l'inserzione degli strumenti è riportata in figura A1.1
 ;
;
 ;
;
 ;
;
ricordando che, essendo il sitema simmetrico e il carico equilibrato, i moduli delle tensioni stellate, delle correnti e l'angolo di sfasamento tensione-corrente, sono uguali (vedi diagramma vettoriale), sperando che mi si perdoni la "licenza poetica" per aver indicato con W1,W2,W3 le potenze attive, in watt, misurate dagli strumenti.
In tal caso la potenza complessiva del carico rappresentato dalle tre impedenze uguali, altro non sarà che la somma delle tre letture:

Nel caso di sistema a tre fili con neutro (che dovrebbero essere quattro fili, ma avendo perso il filo non mi raccapezzo più) l'inserzione degli strumenti è riportata in figura A1.2
Anche in questo caso ogni wattmetro è sottoposto alla tensione stellata e attraversato dalla corrente relative alla fase su cui è inserito ed anche qui le misure sono le seguenti:
 ;
;
 ;
;
 ;
;
con la solita "licenza poetica" sull'indicazione degli strumenti.
Il sistema è simmetrico quindi le tensioni stellate hanno lo stesso modulo, il carico è squilibrato quindi su ogni fase si ha una diversa corrente e un diverso safasamento tensione-corrente, come da diagramma vettoriale. La potenza complessiva del carico rappresentato dalle tre impedenze questa volta diverse (il carico è squilibrato), sarà la somma delle tre letture:

Appendice 2: Un paio di cose sul calcolo della potenza in trifase
Se vale  ,
,
essendo che il modulo della tensione stellata E e il modulo della tensione concatenata V sono correlati dalla relazione  , si ha che
, si ha che

quindi per un carico equilibrato, la potenza attiva è

analogamente la potenza reattiva è

Poiché potenza attiva e reattiva sono in rapporto fra loro come i due cateti di un triangolo rettangolo, si può immagginare anche una ipotenusa che rappresenta la potenza apparente:

Appendice 3: Due Wattmetri
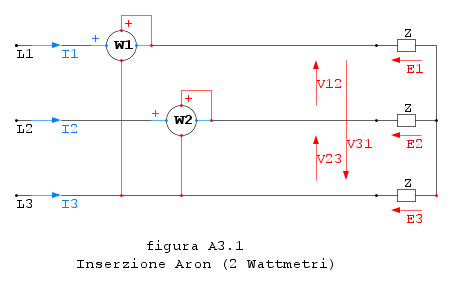
In presenza carico equilibrato alimentato da terna simmetrica (tre fili, il neutro non serve), è possibile utilizzare due soli wattmetri per determinare la potenza: Tale metodo prende il nome di inserzione Aron, chiamata così perchè un certo Hermann Aron invece di pensare ai fatti suoi (come disse un alunno svogliato, cioè io) si mise in testa di risparmiare un wattmetro. L'inserzione Aron prevede il collegamenti degli strumenti come in figura A3.1
In tal caso le misure sono:
 ;
;
 ;
;
con:
 , l'angolo tra la V13 e I1 rispettivamente tensione e corrente nel wattmetro W1;
, l'angolo tra la V13 e I1 rispettivamente tensione e corrente nel wattmetro W1;
 , l'angolo tra la V23 e I2 rispettivamente tensione e corrente nel wattmetro W2;
, l'angolo tra la V23 e I2 rispettivamente tensione e corrente nel wattmetro W2;
come del resto si dovrebbe evincere dal diagramma vettoriale di figura A3.2 (al contrario, se poi che poi non si capisce si eperde...)
Allora:
 ;
;
 ;
;
In quanto i moduli delle concatenate e delle corenti sono uguali.
Non conosco la trigonometria ma se la conoscessi sarei sicuro che andando a sommare le due misure otterrei proprio la potenza del carico pertanto

Aron avrà avuto anche idee strane, però qualcosa ha ottenuto. Ma c'è di più: non solo questo metodo è valido anche per carichi squilibrati purché la rete sia priva di neutro ma è anche possibile determinare la potenza reattiva del carico.
MA NON SI ERA DETTO CHE I WATTMETRI MISURANO SOLO LA POTENZA ATTIVA?
Certo che si era detto ma si riesce comunque a ricavare una potenza reattiva dalla misura delle suddette potenze attive, basta applicare la seguente semplice relazione:

Questa relazione però può utilizzarsi solo nel caso di carichi equilibrati.
Nella relazione W1 è il wattmetro che da una lettura maggiore: wattmetro maggiore, W2 è il wattmetro che da una lettura minore: wattmetro minore.
__________________________________________________________________
nota 1
Gli angoli α e β sopra riportati si riferiscono al diagramma vettoriale della figura, è chiaro che in caso di sfasamenti diversi si potrebbe avere, ad esempio  e
e  . In tal caso è facile intuire che la sostanza del discorso non cambia e che il risultato finale condurrà alla determinazione della potenze attiva e reattiva con le stesse relazioni su scritte.
(Da notare che in questa nota si è cercato di scrivere come in un libro stampato...)
. In tal caso è facile intuire che la sostanza del discorso non cambia e che il risultato finale condurrà alla determinazione della potenze attiva e reattiva con le stesse relazioni su scritte.
(Da notare che in questa nota si è cercato di scrivere come in un libro stampato...)
nota 2
Si va a effettuare la somma
![P=W_1+W_2=[V\cdot I \cdot \cos(30^{\circ}-\varphi)]+[V\cdot I \cdot \cos(30^{\circ}+\varphi)]=\sqrt{3} \cdot V\cdot I \cdot \cos \varphi](/mediawiki/images/math/6/d/c/6dceb2349f559878cd32d6059bbba684.png)
che è prorpio l'espressione della potenza attiva in trifase.
Si va a effettuare la differenza
![W_1-W_2=[V\cdot I \cdot \cos(30^{\circ}-\varphi)]-[V\cdot I \cdot \cos(30^{\circ}+\varphi)]= V\cdot I \cdot \sin \varphi](/mediawiki/images/math/e/b/a/ebabf32df52e0fb04f0f7b8fb809a7d0.png)
che a meno della  è prorpio l'espressione della potenza reattiva in trifase.
è prorpio l'espressione della potenza reattiva in trifase.
__________________________________________________________________
Appendice 4: Un wattmetro
Lo si era intravisto precedentemente.
Ma cosa misura il wattmetro insetrito come in figura A4.1(e dalli con le domande autoposte!!!)?
Misura:

che ha la forma di una potenza reattiva...
Gli angoli sono riportati nel seguente diagramma vettoriale (figura A4.2)
Un wattmetro così collegato si dice "in quadratura".
Appendice 5: E per finire: ancora tre wattmetri
E dopo aver faticato tanto a utilizzare due wattmetri invece di tre si ricomincia a utilizzarne nuovamente tre ma questa volta si parte dall'inserzione Aron e se ne aggiunge unao in quadratura, così, tanto per mischiar le cose e vedere cona ne vien fuori. Chiamasi codesto collegamento dei tre strumenti Inserzione Righi , figura A5.1.
La domanda è la solita: cosa misuramo i tre strumenti?
Risposta:
 ;
;
 ;
;
 ;
;
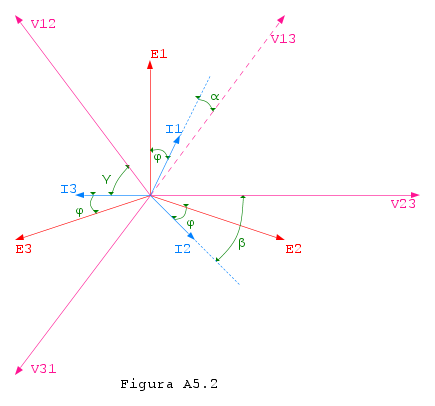
con:  , gli angoli riportati in figura A5.2.
, gli angoli riportati in figura A5.2.
Ne risulta che le potenze del carico sono:
 la potenza attiva (sempre quella in watt);
la potenza attiva (sempre quella in watt);
 la potenza reattiva (sempre quella in var)
la potenza reattiva (sempre quella in var)
inoltre:
- W1 è la misura del wattmetro maggiore;
- W2 la misura del wattmetro minore;
- W3 La misura del wattmetro in quadratura.
Tale inserzione permette di rilevare tramite la misura fornita dai wattmetri sia la potenza attiva che quella reattiva sia nel caso di carichi equilibrati che nel caso di carichi squilibrati, sempre però con la terna di alimentzione simmetrica. Tale possibilità era negata dall'inserzione Aron che permetteva il rilievo della potenza reattiva solo ne caso di carichi equlibrati.
__________________________________________________________________
nota 1
essendo:



si avrà:


Sostituendo queste espressioni in quelle sopra scritte, utilizzate per calcolare le potenze, dopo opportune ed oculate manipolazioni matematico-trigonometriche si otterrà proprio ciò che ci si aspetterebbe per il calcolo delle potenze a seconda che il carico sia equilibrato o meno.
nota 2
per gli angoli si veda quanto già espresso nel caso dell'inserzione Aron
__________________________________________________________________
FINALE (visto che conclusioni l'avevo già scritto)
Sequenza di domande di marzullliana memoria (mi faccio domande e poi mi do una risposta).
- D: Quelle sopra dette sono le uniche possibilità di collegamento dei wattmetri nei sistemi trifase?
- R: Magari!
- D: La trattazione matematica sopra descritta è quella rigorosa?
- R: Magari!!
- D: Il testo sopra esposto è privo di errori?
- R: Magari!!!
- D: I diagrami vettoriali sono disegnati con precisione?
- R: Magari!!!!
- D: ha davvero una sua utilità questo articolo?
- R: Magari!!!!!
- D: Questo sarà il mio ultimo articolo sul blog?
- R: Dopo che gli amministratori del sito lo avranno letto SI!
Bibliografia
- G. Conte - Elettrotecnica Generale (II ed.) - Hoepli
- L. Olivieri, E.Ravelli - Elettrotecnica (vol.1 - I ed. 1995) - CEDAM
- Praticamente tutto ElectroYou per quanto riguarda la sezione dedicata all'elettrotecnica

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)