ElectroYou - la comunità dei professionisti del mondo elettrico

Indice

1 Introduzione
2 Dai generatori alle onde
- 2.1 Analizziamo la cosa in dettaglio
3 I particolari delle onde
- 3.1 Valore efficace
- 3.2 Lo sfasamento
4 Potenza attiva
5 Potenza reattiva
6 Potenza apparente
7 Conclusioni
8 Bibliografia

Introduzione

Ci sono molte spiegazioni analitiche per la corrente alternata, ma visto che sono Tony Stark preferisco puntare a cose più concrete: partiremo quindi dai generatori e da come nasce la corrente stessa...

Dai generatori alle onde

Immaginate di prendere due magneti permanenti, e di fissarli accostando - l'una di fronte all'altra - la parte SUD e quella NORD

Così facendo si verrà a creare un campo magnetico, le cui linee di forza saranno, almeno nella zona centrale, perpendicolari alla due facce.
Ora inserite una spira circolare di sezione S, tra le due facce, nella zona centrale perpendicolarmente alle linee del campo. La "quantità" delle linee che attraversano la spira, che chiameremo flusso magnetico concatenato con la spira, indicandolo con Φ, la poniamo uguale al prodotto dell'intensità del campo B detta induzione magnetica, che consideriamo costante, per la superficie S.

Facendo ruotare la spira attorno all'asse diametrale che passa tra i terminali indicati in figura in senso antiorario, essa offrirà al campo magnetico una superficie sempre minore. Quando forma un angolo $\alpha\ = \frac{\pi}{2}$ rispetto alla posizione iniziale, nessuna linea del campo attraversa la spira, perché le linee sono parallele alla superficie (vedi terza figura). Proseguendo nella rotazione, la spira si porterà ad un angolo $π$ , poi a $\frac{3}{2}\pi$ e infine, dopo un intero giro, quindi per $α = 2π$ torna nella posizione iniziale individuata da $\alpha\ = 0$

rotazione della spira

La superficie effettivamente attraversata dalle linee del campo magnetico, risulta allora pari alla superficie totale dalla spira S per il coseno dell'angolo formato dalla spira stessa rispetto alla sua posizione di partenza, mostrato nella figura seguente.

Analizziamo la cosa in dettaglio

La spira si trova nella posizione iniziale con $[α = 0]$ . Il flusso vale $B S cos(α = 0) = B S$ ricordando che $cos(α)$ con $α = 0$ dà 1; e difatti, quando la spira è orizzontale tutta la sua superficie è attraversata dal campo B.
La spira ruota progressivamente fino a portarsi in posizione verticale $[\alpha = \frac{\pi}{2}]$ . Il flusso vale $Φ = B S cos(α) = 0$ . Il coseno diminuisce da 1 a 0 e, come si può vedere dal disegno, la quantità di linee di campo che attraversa la spira diminuisce. Quando si dispone verticalmente $(\frac{\pi}{2})$ , nessuna linea del campo l'attraversa.
La spira supera la posizione verticale fino a tornare orizzontale per $α = π$ .Il flusso vale in tal caso $Φ = B S cos(α = π) = - B S$ . Il coseno in questa fase è negativo, quindi anche il flusso. Ciò significa che le linee del campo attraversano la spira entrando dalla faccia opposta. Quando la spira si posiziona orizzontalmente, tutta la superficie S sarà attraversata dalle linee di forza.
La spira continua il suo cammino fino a riportarsi in posizione verticale per $[\alpha =\frac{3}{2} \pi]$ . Il flusso vale $\Phi = BS \cos(\alpha = \frac{3}{2} \pi) = 0$ .Il coseno, dal suo massimo negativo torna al valore nullo: coseno di $\frac{3}{2} \pi = 0$ . La spira offre nuovamente superficie nulla al campo.
La spira con $α = 2π$ , ritorna nella posizione iniziale $α = 0$ . Il flusso vale $Φ = B S cos(α = 2π) = B S$ . Il coseno in questa fase aumenta fino ad 1, quando la spira offre l'intera superficie al campo magnetico.

La spira ha completato un giro. Ogni giro successivo si svolge in modo identico.
Rappresentiamo in un diagramma temporale l'evoluzione del flusso.

La legge di Faraday-Neumann-Lenz ci dice che in una spira attraversata da un flusso Ф variabile nel tempo, si viene a creare una forza elettromotrice indotta. Ricordando che l'angolo $α$ può essere visto come la velocità angolare $ω$ di rotazione della spira per il tempo [α=ωt], possiamo derivare il flusso rispetto al tempo e ricavare la f.e.m. $e (t)$ , misurabile con un voltmetro collegato ai terminali della spira.

$e(t)=-\frac{\text{d}\Phi}{\text{d}t}$

$e(t)=-\frac{\text{d} BS \cos(\alpha )}{\text{d}t}$

$e(t)=-BS \frac{\text{d} \cos(\omega t)}{\text{d}t}$

$e(t)= -BS \frac{\text{d} \cos(\omega t)}{\text{d}t}$

$e (t) = B S sin(ω t)$

Come possiamo vedere la tensione $v = e (t) = B S sin(ω t)$ è, come il flusso, funzione sinusoidale del tempo.

I particolari delle onde

D’ora in poi possiamo abbandonare la nostra spira, il nostro campo magnetico e tutto il resto, per concentrarci unicamente sulla tensione variabile nel tempo con legge sinusoidale, analizzarne gli aspetti ed i parametri fondamentali per poter comprenderne gli effetti.

Come si può osservare, v varia tra due valori massimi, $\ V_m$ e $\ -V_m$ ; questi valori corrispondono a B S del paragrafo precedente, pertanto possiamo riscrivere v come $V m sin(ω t)$ .
La rappresentazione temporale della v ci mostra come l'andamento della tensione si ripeta in modo regolare. E' possibile individuare un periodo T in cui la tensione si ripete. Il periodo è individuato come in figura, ma può essere misurato come la distantza temporale fra due picchi positivi (o negativi) ecc...
Esso ci indica in quanto tempo la tensione compie una variazione completa. Sostituendo nell'argomento del seno T a t, possiamo ricavare il valore della pulsazione, che è la velocità angolare della nostra spira:

$\ \omega T\ =\ 2\pi$

$\ \omega \ =\ \frac{2\pi}{T}$

Il numero di periodi compresi nell'unità di tempo, è una nuova grandezza: la frequenza.

$\frac{1}{T} \ =\ f$

Tale grandezza viene misurata in $\ s^{-1}$ (secondi alla meno uno), unità di misura cui viene dato il nome di hertz (Hz), in onore del fisico tedesco Heinrich Hertz (1857-1894).
La pulsazione ω è collegata alla frequenza tramite la formula precedentemente. Quindi

$\omega = \frac{2\pi}{T} = 2 \pi f$

La frequenza indica il numero di variazioni complete della tensione nell'unità di tempo.
In Italia la tensione di rete varia con una frequenza di 50Hz, ossia in un secondo la tensione compie 50 periodi completi. In altri paesi la frequenza di rete è diversa. Negli Stati Uniti è di 60Hz.

Valore efficace

Osservando il grafico di una tensione sinusoidale ci si accorge immediatamente che il valore medio in un periodo è nullo in quanto l'area sottesa nel semiperiodo positivo è identica a quella sottesa nel semiperiodo negativo: ne risulta una somma ovviamente nulla.
A livello matematico ciò è ancora più immediato in quanto l'integrale di un seno tra 0 e 2 $π$ dà risultato nullo.
Questo però non deve far credere che la potenza trasportata sia nulla: la potenza infatti va con il quadrato della tensione;

$\ P\ =\ \frac{V^2}{R}$

La potenza assume quindi valori positivi in tutto il periodo; perciò possiamo ad esempio calcolare l'energia $W R$ spesa in un periodo su una resistenza R, come l'energia dissipata sulla stessa resistenza da una tensione continua di valore V, che è il valore efficace della grandezza alternata.
Avremo quindi:

$\int_{0}^T {\frac{v^2(t)}{R} \text{d}t}=W_R =\ \frac{V^2}{R} T$

Per ricavare il valore di $V$ occorre perciò calcolare $W R$ , moltiplicarla per R dividerla per il periodo T ed estrarne la radice quadrata.

$V=\sqrt{\frac{R W_R}{T}}=\sqrt{\frac 1 T \int_{0}^T {v^2(t) \text{d}t}}$

quindi

$V^2 T = \int_{0}^{T}{ v^2(t) \text{d} t}$

Occorre perciò integrare $\ v^2(t)$ nel periodo T. L'integrale non è banale (almeno per me :-( ) i conti che seguono sono noiosi (sempre per me) e consiglio, se non interessati (come me), di saltarli. Ad ogni modo, per i più volonterosi ( mi piace scherzare :-)) eccoli. Spero siano corretti, altrimenti, oltre a beccarmi altri strali (già me ne sono arrivati) di admin, la reputation mi crolla! :-|, anche se sono Iron Man: qui non guardano in faccia nessuno! :-) )

$\int_{0}^{T} v^2\, \text{d}t \ =\ \int_{0}^{T} {V_m}^2\ \sin^2(\omega t)\ \text{d}t$

Ricordando che:

$1-2\sin^2 \alpha \, =\ \cos 2 \alpha$

Si ottiene allora, con qualche aggiunta e sottrazione:

$V^2 T = \int_{0}^{T} {V_m}^2\ \sin^2(\omega t)\frac{2}{2}\ \text{d}t = {V_m}^2\ \frac{1}{2}\int_{0}^{T} 2\ \sin^2(\omega t)\ \text{d}t =$
$={V_m}^2\ \frac{1}{2}\int_{0}^{T} \left ( 1-1+2\sin^2(\omega t)\ \right ) \text{d}t =$
$= -\frac{1}{2} {V_m}^2 \int_{0}^{T} \left( -1+1\ -2\sin^2(\omega t) \right ) \text{d}t=$
$= -\frac{1}{2} {V_m}^2(-T+\int_{0}^{T}\left ( 1 -2 \sin^2(\omega t) \right ) \text{d}t)=$
$={V_m}^2 \left ( \frac{T}{2}-\frac{1}{2} \int_{0}^{T} \left ( 1 -2 \sin^2(\omega t) \right ) \text{d}t \right )=$
$=\frac{1}{2} {V_m}^2 \left ( T-\int_{0}^{T} \cos(2\omega t)\ \text{d}t \right )= \frac{1}{2} {V_m}^2 ( T - 0 )$
Si ha perciò

${V_m}^2\ \frac{1}{2}\ =\ V^2$

dalla quale otteniamo semplicemente il risultato:

$V = \frac{{V_m}}{\sqrt{2}}$

Questo valore è detto valore efficace.
Un modo più pratico per ottenerlo è tramite una misura diretta: solitamente amperometri e voltmetri misurano direttamente il valore efficace delle rispettive grandezze, mentre un oscilloscopio mostra la funzione nella sua interezza con il suo valore massimo. Facendo il rapporto tra le due misure risulta un fattore $\sqrt{2}$ pari a circa 1,41....
La tensione di rete è di 220V in valore efficace. Con un semplice calcolo è possibile vedere la tensione massima o di picco pari a :

$V_m\ =\ 220\sqrt{2}\ =\ 311$
I valori efficaci di corrente e tensione si scrivono semplicemente con la lettera maiuscola senza alcun pedice: I, V. Ma è anche possibile trovarli nei testi anglosassoni con il pedice RMS.
E' quindi possibile scrivere il valore massimo come $\sqrt{2} V$ ; di conseguenza $v\ =\sqrt{2} V \sin (\omega t)$

Lo sfasamento

Facciamo ora un ultimo passo. L'immagine in alto, ci pone di fronte ad un problema: entrambe le funzioni hanno lo stesso periodo, quindi stessa frequenza f e pulsazione $\ \omega$ , ed hanno anche lo stesso valore massimo.
Secondo quanto abbiamo visto fino ad ora, entrambe le funzioni verrebbero espresse identicamente come ${V_m}\ \sin (\omega t)$ ; ma come è evidente dal grafico, si tratta di due funzioni totalmente distinte.
Come si può vedere, la prima funzione parte un po’ prima della seconda. Indichiamo tale intervallo di tempo con Tx, e, ad esso, associamo un angolo $\ \varphi$ , che definisce lo sfasamento tra le due sinusoidi.
Sapendo che in un periodo T viene descritto un angolo $\ 2\pi$ , possiamo impostare una proporzione per individuare il $\varphi$ che corrisponde a Tx;

$\frac{2\pi}{T}\ =\ \frac{\varphi}{T_x}$

Quindi

$\varphi\ = 2\pi \frac{T_x}{T}$

Una generica funzione sinusoidale, potrà allora essere scritta con $v = {V_m} \sin(\omega t\pm \varphi)$ o, utilizzando il valore efficace, con $v = \sqrt{2}V \sin(\omega t\pm \varphi)$ . Nel caso della sinusoide che stiamo considerando, il segno è "+" perché per t=0, cioè nell'origine, essa è positiva. Un angolo di fase φ = 0 corrisponde ad una sinusoide che passa per l'origine degli assi.
Tutto ciò che è stato detto fino ad ora può essere riferito ugualmente sia alla corrente sia alla tensione, per cui avremo:
$v = {V_m} \sin(\omega t\pm \phi) \ \ \Rightarrow \ \ i = {I_m} \sin(\omega t\pm \phi)$
$v = \sqrt{2}V \sin(\omega t\pm \phi\ \ \Rightarrow \ \ i = \sqrt{2}I \sin(\omega t\pm \phi)$

Potenza attiva

Pensiamo adesso ad una corrente ed una tensione alla stessa frequenza e con costante di fase $\varphi \ = \ 0$ , su di un carico resistivo (una resistenza). Esse svilupperanno una potenza sempre positiva come mostrato precedentemente ed in figura.

La potenza media $\ P$ in un periodo è uguale alla metà del picco di potenza, che indichiamo con $Π$ .

$P = \frac{\Pi}{2}$

Il picco di potenza è pari al prodotto della tensione massima per la corrente massima:

$\Pi\ =\ {V_m} {I_m}$

Ricordando che il valore massimo corrisponde al valore efficace per radice quadrata di due, cioè

$V_m = \sqrt{2}V \quad {I_m}\ =\ \sqrt{2}I$

sostituendo otteniamo

$P = \frac{{V_m I_m }}{2} = \frac{{\sqrt 2 V\sqrt 2 I}}{2} = VI$

Questi risultati erano ricavabili dalla stessa definizione di valore efficace che abbiamo dato nei paragrafi precedenti, ossia di un valore che dovrebbe avere una grandezza continua per trasportare la stessa potenza della nostra grandezza alternata. Tenendo questo a mente possiamo scrivere la legge di Ohm

V = R I

e quella di Joule

$P = V I = R I^2 = \frac{V^2}{R}$

La potenza dissipata in questo modo sulla resistenza produrrà del calore per effetto Joule in modo analogo ad una corrente continua e, come la potenza in corrente continua, la potenza attiva viene misurata in watt [W]

Possiamo infine osservare che la potenza attiva ha una frequenza doppia rispetto a quella della corrente e della tensione, come si evince in figura; quindi, prendendo ad esempio le grandezze di rete, avremo la tensione con frequenza 50 Hz e potenza con frequenza doppia, pari a 100 Hz.

Potenza reattiva

Proviamo ora a sfasare con un angolo $\varphi = \frac{\pi}{2}$ la corrente rispetto alla tensione.

Anche in questo caso la frequenza della potenza risulta doppia rispetto a quella della tensione o della corrente, ma in questo caso il suo valore non è sempre positivo, anzi risulta una sinusoide a valore medio nullo. Ciò significa che non risulta alcuna produzione di calore, come visto in precedenza, né di lavoro.
Analizzando più in dettaglio tale fenomeno possiamo dividere il periodo in quattro parti, come indicato in figura.

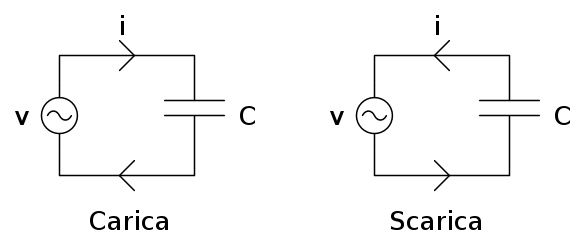
Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

La tensione parte da zero e raggiunge il suo picco positivo, mentre la corrente cala dal suo picco positivo progressivamente fino a raggiungere lo zero. Come è evidente la somma di tali onde genera un semiperiodo di sinusoide. A livello fisico possiamo considerare questa fase come la carica di un condensatore effettuata con un valore di tensione ai capi variabile nel tempo. Nell'istante in cui comincia la carica il condensatore è scarico, per cui la corrente fluisce liberamente e va a caricare le armature dello stesso ai capi delle quali compare la tensione v.Man mano che il tempo passa le armature si caricano e la corrente che trasporta tale carica diminuisce, come il flusso di persone all'interno di un cinema sempre più pieno: all'inizio molte persone possono entrare e sedersi ma man mano che la sala si riempie, sempre meno persone trovano poltrone libere. Quando il condensatore è completamente carico la tensione è massima e la corrente è nulla. Per caricare il condensatore occorre energia che è fornita dal generatore.
La tensione parte dal suo valore massimo positivo e decresce fino a zero, mentre la corrente parte da zero e raggiunge il suo massimo negativo. Riprendendo l'esempio precedente, il condensatore eroga corrente verso il generatore la cui tensione v è minore di quella del condensatore. Una volta scaricato, il condensatore avrà ai propri capi una tensione nulla e erogherà la massima corrente negativa, (cioè contraria alla fase precedente dove è assunta come positiva). Nella sua scarica il condensatore restituisce al generatore tutta l'energia da esso fornitogli nel periodo di carica.
La tensione assume valori negativi partendo da zero ed arrivando al picco negativo, mentre la corrente prosegue il suo cammino dal picco negativo fino allo zero. La risultante è pari alla semionda positiva vista in precedenza al punto 1. In questo caso abbiamo una nuova carica del condensatore, con l'unica differenza che il tutto avviene in maniera "capovolta" rispetto alla precedente; tale carica sarà ovviamente fornita dal generatore, che quindi dovrà erogare nuovamente energia.
Infine la tensione risale fino ad incrociare l'asse dei tempi mentre la corrente risale fino al suo picco positivo. In questo caso, vista l'inversione di segno della corrente, risulterà un nuovo semiperiodo negativo. Il nostro condensatore tornerà a scaricarsi sul generatore restituendo la potenza acquistata per la propria carica.

Nel periodo completo T, la potenza erogata dal generatore e quella ad esso restituita dal condensatore, coincidono perfettamente dando luogo ad un bilancio nullo, per cui la potenza reattiva non potrà essere utilizzata né per generare calore né lavoro, in quanto risulta un "rimpallo" di carica tra il generatore ed il condensatore. Tutto questo è puramente a livello teorico in quanto ogni condensatore reale possiede internamente delle perdite che dissiperanno energia.

Ora vedremo il caso in cui lo sfasamento, tra la corrente e la tensione, sia pari a $\ \varphi\ =\ -\frac{\pi}{2}$ ; in questo caso dal punto di vista fisico il carico sarà formato esclusivamente da un induttanza.

potenzaR2.JPG

Come si evince dal grafico, la potenza in questo caso risulta invertita di segno rispetto a quella precedentemente vista, ed il suo valor medio risulta perfettamente nullo.

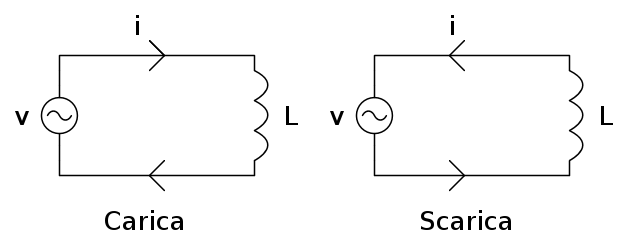
In questo caso possiamo vedere tale fenomeno come la progressiva carica e scarica di un induttore; questa volta non sarà l'energia elettrostatica ad essere immagazzinata, bensì quella magnetica generata dalla corrente.
In questo caso, nel secondo e quarto semiperiodo l'induttanza viene caricata dall'aumento della corrente verso i valori di picco; mentre nel primo e terzo essa eroga energia al generatore.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Come detto, in entrambi i casi la potenza media generata è nulla, anche se uno scambio di energia si è verificato. Per tenerne conto definiamo la potenza reattiva $Q$ come il prodotto dei valori efficaci della tensione e della corrente in quadratura, cioè sfasata di $\varphi = \frac{\pi}{2}$

Q = V I

Essa viene misurata in var, volt ampere reattivi, e viene presa come convenzione positiva per carichi induttivi, negativa per carichi capacitivi.

Potenza apparente

Nella maggior parte dei casi non avremo un angolo di sfasamento $\ \varphi$ pari esattamente a zero o a $\pm \frac{\pi}{2}$ ma un valore intermedio. Prendiamo ora in considerazione il caso in cui l'angolo tra tensione e corrente sia di 60°.

potenzaApp.JPG

In tal caso la potenza non sarà una funzione totalmente positiva, come nel caso della potenza attiva, né a valore medio nullo, come nel caso di quella reattiva; possiamo però immaginarla come somma delle due.
Il modo più semplice per vedere tale legame è quello di anticipare il metodo dei fasori, che verrà analizzato con più attenzione in un prossimo articolo.
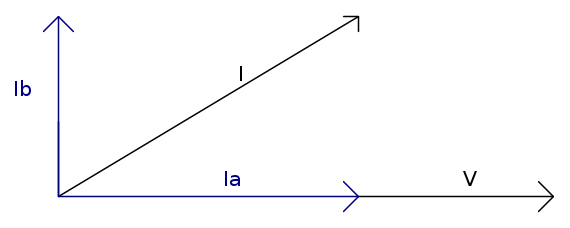
Con questo sistema possiamo vedere la corrente come un vettore inclinato rispetto al vettore con cui rappresentiamo la tensione, del nostro angolo $\varphi$ = 60°; tenendo a mente che un vettore può essere scomposto lungo i due assi, la corrente I può essere scomposta in due vettori $\ I_a$ ed $\ I_b$ .
$\ I_a$ risulta lungo lo stesso asse di V, per cui forma rispetto ad essa un angolo $\varphi \ =\ 0$ ; possiamo quindi desumere che essa sia la componente attiva della corrente iniziale.
$\ I_b$ invece si trova con un angolo $\varphi = \frac{\pi}{2}$ rispetto a V esattamente come la corrente della potenza reattiva.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Definiremo quindi il valore di potenza apparente come quello generato dal prodotto di I V, misurato in volt ampere, con I e V sfasati di un generico angolo $\varphi$
$S\ =\ V\ I$
Ora possiamo dare una nuova definizione generale valida per ogni angolo di sfasamento φ di potenza attiva e di potenza reattiva desumibile dai grafici vettoriali precedenti;

$\text{Potenza Apparente:}\,S = V I \quad \text{VA}$

$\text{Potenza Attiva:}\,P = V I_a = V I \cos \varphi = S \cos \varphi \quad \text{W}$

$\text {Potenza Reattiva:}\, Q = V I_b = V I \sin \varphi = S \sin \varphi \quad \text{var}$

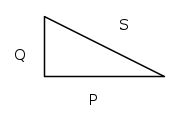
A sua volta S può essere ricavata da P e da Q secondo il seguente procedimento:

$S = VI = V \sqrt{I_a^2 + I_b^2} = \sqrt{V^2 (I_a^2+I_b^2)}=$

$=\ \sqrt{V^2I_a^2 +\ V^2I_b^2} = \sqrt{P^2 + Q^2}$

Le tre potenze possono essere rappresentate a loro volta con tre segmenti che formano un triangolo rettangolo, denominato triangolo delle potenze;

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Nella costruzione di impianti e apparecchi elettrici, si tenta per quanto possibile di far coincidere la potenza apparente con quella attiva, in quanto - come precedentemente detto - la potenza reattiva non è in grado di compiere lavoro. Per fare ciò bisogna ridurre quanto più possibile l'angolo di sfasamento $\varphi$ ; tale procedura è denominata rifasamento.
E' opportuno quindi introdurre il concetto di fattore di potenza;

$\text{Fattore di potenza:} = \frac{P}{S} = \cos(\varphi)$
che indica la quota parte di potenza apparente trasformata su di un carico in potenza attiva, con φ angolo compreso fra la tensione e la corrente.

Conclusioni

Questo modesto articolo è servito più che altro a creare una base a cui rifarmi nei miei successivi articoli, prendere confidenza con il metodo di inserimento stile Wiki e con le formule in Latex, ma soprattutto per permettermi di ripassare e, perché no, approfondire gli argomenti del corso di elettrotecnica che al momento sto seguendo all'università.

Odio i finali tristi, per cui vi dico soltanto... "TORNERÒ"

Bibliografia

ELETTROTECNICA M. D'Amore
ELETTROTECNICA GENERALE G.Licata-D.Favoino
WIKIPEDIA

DISEGNI

ELETTROTECNICA GENERALE G.Licata-D.Favoino
TONY STARK

CORREZIONI

FRANCESCA S.
SIRIA A.
ADMIN

Citazione finale; Terminator

ElectroYou - la comunità dei professionisti del mondo elettrico

Corrente Alternata Sinusoidale

Indice

Introduzione

Dai generatori alle onde

Analizziamo la cosa in dettaglio

I particolari delle onde

Valore efficace

Lo sfasamento

Potenza attiva

Potenza reattiva

Potenza apparente

Conclusioni

Bibliografia

Inserisci un commento

Argomenti correlati

Tag Cloud

Informazioni

Seguici

Pubblicità

Credits