Quale è il modo più semplice per provare/ricavare la relazione di "compensazione"
 , cioè che se questa è vera la fdt sarà semplicemente
, cioè che se questa è vera la fdt sarà semplicemente  indipendente dalla frequenza??
indipendente dalla frequenza??ovviamente i soliti noti sanno cosa fare
Moderatore: ![]() carlomariamanenti
carlomariamanenti
 , cioè che se questa è vera la fdt sarà semplicemente
, cioè che se questa è vera la fdt sarà semplicemente  indipendente dalla frequenza??
indipendente dalla frequenza?? instead of
instead of  (Anonimo).
(Anonimo). ain't
ain't  , right?
, right? in lieu of
in lieu of  .
. for
for  arithm.
arithm.




 si ha un semplice partitore resistivo con
si ha un semplice partitore resistivo con  . Ed è ugualmente immediato verificare che per
. Ed è ugualmente immediato verificare che per  si ritrova invece un partitore capacitivo, con
si ritrova invece un partitore capacitivo, con  .
. che per
che per  , è ovvio che ci sarà anche uno zero.
, è ovvio che ci sarà anche uno zero. .
. , si ricava che sarà
, si ricava che sarà  .
. . Dalla relazione precedente, si ricava allora
. Dalla relazione precedente, si ricava allora  , che equivale a dire
, che equivale a dire  . Elaborando l'espressione, si ottiene la relazione desiderata
. Elaborando l'espressione, si ottiene la relazione desiderata  .
.DoeM ha scritto:Spero di non avere scritto cavolate.

 -
- :
:
 instead of
instead of  (Anonimo).
(Anonimo). ain't
ain't  , right?
, right? in lieu of
in lieu of  .
. for
for  arithm.
arithm.

Spero di non avere scritto cavolate.
 +1
+1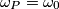 esclusa
esclusa 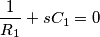
jormay ha scritto:non riesco a linkare i nomi come fate voi
[user]jormay[/user]
Visitano il forum: Nessuno e 3 ospiti