Indice |
Abstract
L'articolo è ricavato dalla lettura dei primi capitoli del testo riportato nella bibliografia.
Lo scopo è di mostrare le considerazioni fisiche e matematiche alla base del processo di conversione dell'energia elettrica in energia meccanica (ed anche viceversa).
Forze elettromeccaniche
Le forze meccaniche di un sistema elettromagnetico si possono determinare esaminando la variazione dell'energia del sistema in conseguenza di uno spostamento della parte sotto osservazione.
E' un metodo comune nell'esame di ogni sistema fisico, basato sul principio di conservazione dell'energia.
Principio di conservazione dell'energia
Per fissare le idee consideriamo un motore elettrico. La conversione elettromeccanica dell'energia elettrica coinvolge naturalmente l'energia elettrica prodotta nel circuito elettrico, l'energia meccanica ottenuta dal motore, l'energia del campo magnetico prodotto dal circuito elettrico, le perdite sotto forma di calore dovute alle resistenze elettriche, agli attriti meccanici e alla ventilazione, all'isteresi ed alle correnti parassite nei circuiti magnetici. Considerando le variazioni a partire da una situazione di regime, possiamo scrivere il principio in questo modo:
![\text{d}W_{el}=\text{d}W_{mecc}+\text{d}W_{campo} \quad [1]](/mediawiki/images/math/b/9/1/b911dea628c7a7fd65007ca8ab7b2dd6.png)
- dWel: variazione dell'energia elettrica disponibile al netto delle perdite elettriche per effetto Joule. Si può in genere esprimere come somme di prodotti eidt essendo e una forza elettromotrice generata nel circuito elettrico ed i la corrente relativa.
- dWmecc: variazione dell'energia convertita in forma meccanica comprensiva delle perdite per attriti. Si può esprimere come somme di prodotti di fvdt con f forza applicata all'elemento meccanico considerato e v velocità relativa, per i moti lineari, oppure in cωdt per i moti rotatori con c coppia agente e ω velocità angolare dell'elemento meccanico considerato
- dWcampo : variazione dell'energia immagazzinata nel campo magnetico, comprensiva delle eventuali perdite nei circuiti magnetici
- Nota: la forma matematica usata è la differenziale, ma l'equazione è valida anche per variazioni non infinitesime
La legge di Faraday-Lenz
Il campo è necessario per la conversione.
Esso si comporta come un serbatoio di energia da cui il sistema meccanico, nel caso si tratti di un motore elettrico, preleva quella che gli è necessaria, ed in cui il sistema elettrico immette quella richiesta in conseguenza della reazione prodotta dal campo.
La reazione si manifesta nel circuito elettrico con la forza elettromotrice espressa dalla legge di Faraday che, considerando il valore assoluto, è data dalla derivata del flusso Φc concatenato con il circuito, cioè dalla velocità con cui esso varia:
![e = \left| {\frac{{{\rm{d}}{\Phi _c}}}{{{\rm{d}}t}}} \right| \quad [1.a]](/mediawiki/images/math/e/b/f/ebfbc53bffc89cb85b59c73a35ce091e.png)
Occorrerà poi tener presente la legge di Lenz, che afferma che la reazione è sempre tale da opporsi alla causa che la produce.
In base alle convenzioni generalmente adottate per i versi positivi di flusso e fem indotta, ciò implica un segno meno nell'equazione per uno dei due termini.
Le strutture che nella pratica generano tecnicamente il campo magnetico sono gli avvolgimenti.
Se indichiamo con N il numero delle spire che compone un avvolgimento, si può definire il flusso medio che attraversa una spira come
Φ = Φc / N.
Schemi a blocchi dei flussi energetici
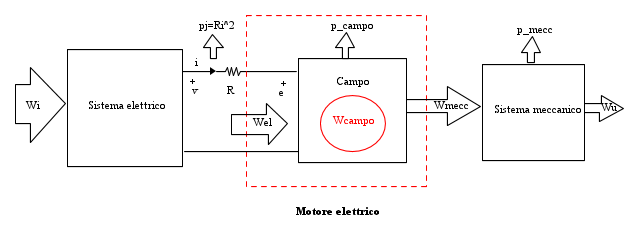
Lo schema a blocchi seguente illustra i flussi energetici nella trasformazione di energia elettrica in energia meccanica (motore elettrico)
Wi è l'energia primaria che può essere di qualsiasi origine a seconda del tipo di generatore.
Si immagina che tutte le perdite elettriche per effetto Joule siano concentrate nella resistenza evidenziata.
Il quadrato in tratteggio delimita la zona cui si riferisce il bilancio energetico espresso dalla [1]
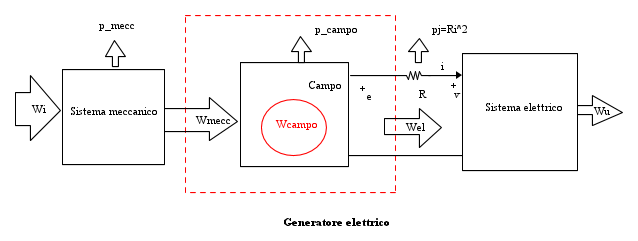
Nel caso si consideri un generatore elettrico, è il sistema meccanico ad immettere energia nel campo e l'elettrico a prelevarla. Lo schema a blocchi cui riferirsi per i flussi energetici è in tal caso il seguente. L'energia elettrica generata è, in questo caso, comprensiva delle perdite nelle resistenze.
Energia del campo magnetico
L'energia immagazzinata in un campo magnetico è legata alla causa che lo produce, in generale una corrente che percorre un avvolgimento.
Al prodotto dell'intensità di corrente per il numero di spire, si dà il nome di forza magnetomotrice (f.m.m:  ) e si misura in ampere.
) e si misura in ampere.
L'effetto è quantificato dal flusso magnetico Φc concatenato con il circuito, che si misura in weber che è volt moltiplicato per secondo, come si deduce dalla [1.a] : Wb = Vs.
Tale energia è funzione del flusso e della configurazione geometrica della struttura tecnica che produce il campo.
Per ogni configurazione geometrica si ha una caratteristica di magnetizzazione, che rappresenta il legame tra flusso magnetico medio e forza magnetomotrice  .
.
I punti della caratteristica di magnetizzazione sono detti punti di lavoro.
La presenza di materiali ferromagnetici determina in genere una caratteristica non lineare, che si ha invece nel caso di campo magnetico completamente in aria.
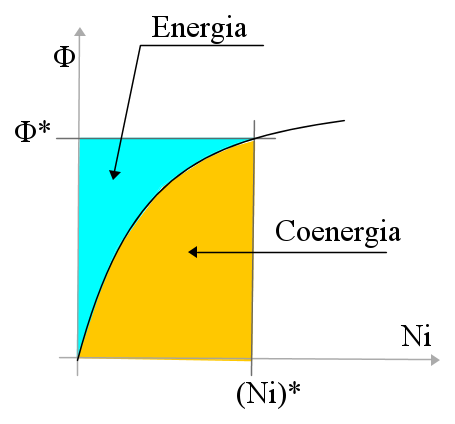
Nel seguente diagramma è rappresentata una tipica caratteristica di magnetizzazione non lineare.
L'area colorata in azzurro, che si calcola con l'integrale  ,
rappresenta l'energia magnetica immagazzinata nel campo prodotto dalla struttura in corrispondenza ai valori Φ * di flusso ed (Ni) * di forza magnetomotrice.
,
rappresenta l'energia magnetica immagazzinata nel campo prodotto dalla struttura in corrispondenza ai valori Φ * di flusso ed (Ni) * di forza magnetomotrice.
Possiamo porre infatti  poiché, se non c'è variazione di energia meccanica, si ha per la [1] dWel = dWcampo ed è, per la legge di Faraday,
poiché, se non c'è variazione di energia meccanica, si ha per la [1] dWel = dWcampo ed è, per la legge di Faraday,  .
.
La variazione di energia elettrica nel circuito, è direttamente legata alla variazione di flusso magnetico, per cui possiamo affermare che l'energia elettrica prodotta dal circuito elettrico, al netto delle perdite ed in assenza di lavoro meccanico, è immagazzinata nel campo magnetico.
L'area colorata in giallo, che si calcola con l'integrale  è detta coenergia, indicandola con W'campo. E' una grandezza utile nei calcoli. La somma di energia e coenergia è l'area del rettangolo di altezza Φ * e base Ni * , quindi
è detta coenergia, indicandola con W'campo. E' una grandezza utile nei calcoli. La somma di energia e coenergia è l'area del rettangolo di altezza Φ * e base Ni * , quindi 
In genere la struttura tecnica prevede la presenza di materiale ferromagnetico che convoglia il flusso magnetico in zone con aria dette traferri.
L'energia totale del campo è la somma di quella del campo nel materiale ferromagnetico e di quella del campo nel traferro.
Spesso è sufficiente, almeno in prima approssimazione, la considerazione del campo magnetico confinato nel traferro.
La considerazione del solo traferro rende lecita una relazione lineare tra flusso e f.m.m:

con k costante dipendente dalla configurazione geometrica del traferro.
Campo lineare
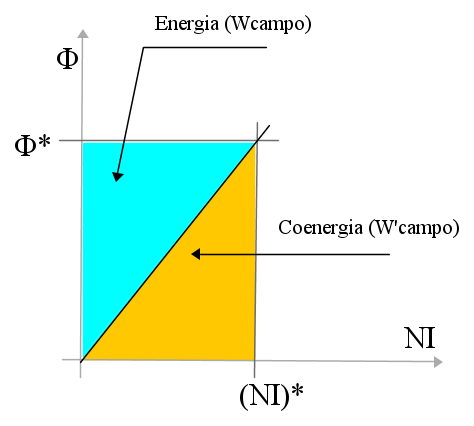
Nel caso in cui il campo sia lineare, energia e coenergia sono uguali.
E' il caso del campo magnetico in aria. Energia e coenergia valgono
![W_{campo}=W'_{campo}=\frac 1 2 \Im \Phi \quad [2]](/mediawiki/images/math/a/b/1/ab141658c65f317aaa4332cfea7c60fb.png)
dove  è la f.m.m. misurata in A (ampere) e Φ il flusso magnetico in Wb (weber) e l'energia in J (joule).
è la f.m.m. misurata in A (ampere) e Φ il flusso magnetico in Wb (weber) e l'energia in J (joule).
- Nota: la formula è scritta per un generico punto di lavoro. Naturalmente, con riferimento alla figura i valori da considerare sono Φ * e Ni *
Energia specifica
Il campo magnetico H è una forza magnetomotrice per unità di lunghezza, quindi  , con l lunghezza della linea di forza del campo ed H il campo medio lungo la linea.
, con l lunghezza della linea di forza del campo ed H il campo medio lungo la linea.
L'induzione magnetica B è un flusso per unità di superficie, quindi Φ = BA, dove A è l'area della superficie attraversata dal flusso e B l'induzione media sulla superficie.
Si può allora scrivere

dove vol = Al è il volume dello spazio occupato dal campo magnetico.
L'energia per unità di volume (o specifica) è dunque definita da
![{w_e} = \frac{1}{2}HB = \frac{1}{2}\mu {H^2} = \frac{1}{2}\frac{{{B^2}}}{\mu } \quad [2.a]](/mediawiki/images/math/8/1/3/8134138053514c9c33c7dfb1ccf56fdb.png)
(ricordando che B = μH dove μ è la permeabilità magnetica)
- Nota: la spiegazione di questi concetti più rigorosa e dettagliata si deve ricavare da un testo di elettromagnetismo. Il precedente è, sostanzialmente, un modo per rinfrescare le formule che dovrebbero essere note a chi si avventura in queste letture.
Introducendo i concetti di
riluttanza

permeanza

coefficiente di autoinduzione

dove si considera un avvolgimento di N spire percorse dalla corrente di intensità i, si hanno le espressioni
![W_{campo}=W'_{campo}=\frac 1 2 \Re \Phi^2=\frac 1 2 \wp \Im^2=\frac 1 2 Li^2 \quad [3]](/mediawiki/images/math/0/2/f/02ffd33ed11ec6139917154e11def433.png)
Energia meccanica
Una variazione della configurazione geometrica, corrisponde al passaggio da una caratteristica di magnetizzazione ad un'altra.
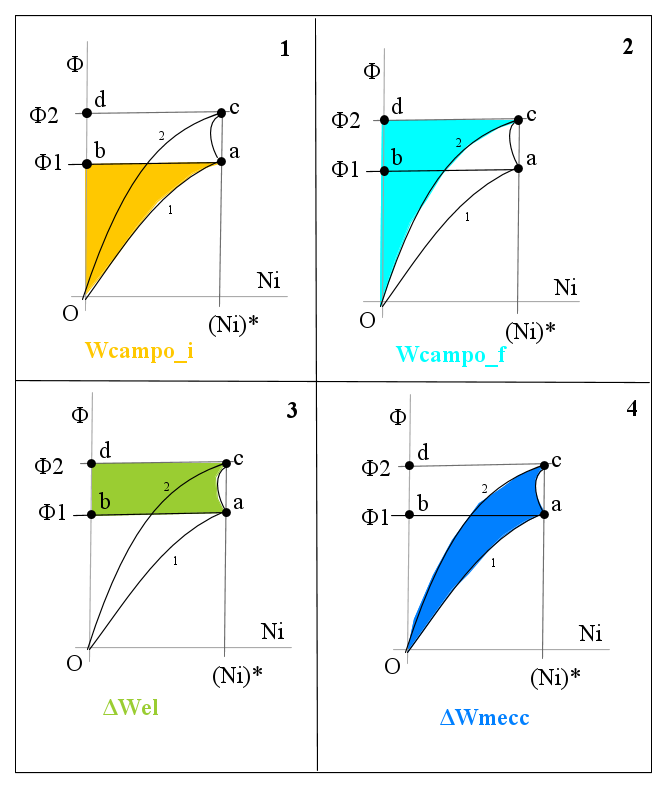
Nella figure seguenti si ipotizza che il sistema in esame si trovi inizialmente nella situazione cui corrisponde la curva di magnetizzazione 1 e, dopo la variazione, nella configurazione corrispondente alla curva di magnetizzazione 2.
Si suppone che la forza magnetomotrice iniziale (Ni) * sia uguale a quella finale, mentre il flusso passa dal valore Φ1 al valore Φ2. Durante questo passaggio varia la forza magnetomotrice per effetto della tensione indotta nel circuito che la produce, quindi esisterà un legame tra Φ e  che è estremamente complicato ricavare matematicamente. Possiamo osservare che se la tensione indotta è trascurabile, il che significa una piccola velocità meccanica, la corrente, quindi la fmm è praticamente costante e la transizione avviene in pratica secondo il segmento verticale ac. Più la velocità meccanica è elevata, maggiore è la fem indotta che diminuisce, per la legge di Lenz, la forza magnetomotrice, per cui la curva di transizione piega verso sinistra. Possiamo perciò rappresentare la transizione con una curva del tipo di quella disegnata che unisce i punti a e c.
che è estremamente complicato ricavare matematicamente. Possiamo osservare che se la tensione indotta è trascurabile, il che significa una piccola velocità meccanica, la corrente, quindi la fmm è praticamente costante e la transizione avviene in pratica secondo il segmento verticale ac. Più la velocità meccanica è elevata, maggiore è la fem indotta che diminuisce, per la legge di Lenz, la forza magnetomotrice, per cui la curva di transizione piega verso sinistra. Possiamo perciò rappresentare la transizione con una curva del tipo di quella disegnata che unisce i punti a e c.
- Nella figura 1, l'area gialla corrisponde all'energia inizialmente immagazzinata nel campo magnetico:
 ;
;
- nella figura 2, l'area ciano corrisponde all'energia finale immagazzinata nel campo magnetico:

- nella figura 3, l'area verde corrisponde all'energia elettrica messa in gioco nel circuito durante la variazione:
 ;
;
- nella figura 4, l'area blu si ricava dalla relazione

Per la [1] è ΔWmecc = ΔWel − ΔWcampo per cui l'area blu corrisponde all'energia meccanica messa in gioco nella trasformazione.
Questo è un risultato molto importante che permette di ricavare espressioni matematiche per la forza elettromeccanica.
Espressioni per la forza
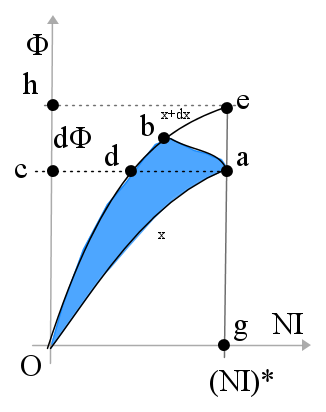
Nella figura precedente la configurazione iniziale è individuata dalla variabile x, mentre una variazione determinata da uno spostamento dx nella direzione della forza f, porta alla configurazione corrispondente alla curva indicata con x + dx, ipotizzando che lo spostamento dx implichi un aumento del flusso magnetico a parità di forza magnetomotrice.
Il punto di lavoro nella configurazione x è a, mentre quello nella configurazione x + dx è b.
La variazione di energia meccanica, cioè il lavoro meccanico compiuto dalla forza f nello spostamento dx corrisponde, per quanto mostrato nel paragrafo precedente, all'area blu: OabO
Tale area differisce dall'area OadO per l'area dab, area, quest'ultima, che tende a zero in quanto dipende da dx.
L'area blu evidenziata può allora essere considerata uguale all'area OadO, molto più semplice da calcolare, in quanto differenza delle aree OacO ed OdcO che rappresentano, rispettivamente, l'energia magnetica iniziale e l'energia magnetica finale, se il flusso Φ è costante.
Esprimendo allora l'energia magnetica in funzione del flusso Φ e della variabile x, si può affermare che il lavoro compiuto dalla forza f corrisponde al decremento dell'energia immagazzinata nel campo  :
:
fdx = − dWcampo(Φ,x)
La forza è pertanto esprimibile come la derivata parziale della Wcampo(Φ,x) fatta rispetto ad x
![f = - \frac{{\partial {W_{campo}}}}{{\partial x}}(\Phi ,x) \quad [4]](/mediawiki/images/math/9/5/6/95636d5bc727dd9b6ead27c932eaed41.png)
Si può anche osservare che l'area blu differisce dall'area OaeO per l'area abe che, dipendendo da dx, tende a zero.
L'area OaeO è la differenza tra le aree OgeO ed OgaO che sono, rispettivamente, la coenergia finale ed iniziale del campo, considerando costante la forza magnetomotrice.
Esprimendo la coenergia in funzione della forza magnetomotrice  e della variabile x, si può affermare che il lavoro compiuto dalla forza f corrisponde all'incremento della coenergia del campo:
e della variabile x, si può affermare che il lavoro compiuto dalla forza f corrisponde all'incremento della coenergia del campo:

La forza è pertanto esprimibile come la derivata parziale della  fatta rispetto ad x
fatta rispetto ad x
![f = \frac{{\partial {W'_{campo}}}}{{\partial x}}(\Im ,x) \quad [5]](/mediawiki/images/math/5/b/f/5bf0520c4287fba1728e96022aba3fdc.png)
Campo lineare
In aria, riluttanza, permeanza, coefficiente di autoinduzione sono delle costanti.
Se  ,
,  od L dipendono da una variabile x, le [3], tenendo conto che la prima è una funzione del flusso oltre che della variabile x, le altre due invece lo sono della forza magnetomotrice e della variabile x, consentono di ricavare la forza con le espressioni
od L dipendono da una variabile x, le [3], tenendo conto che la prima è una funzione del flusso oltre che della variabile x, le altre due invece lo sono della forza magnetomotrice e della variabile x, consentono di ricavare la forza con le espressioni
![f = - \frac{1}{2}{\Phi ^2}\frac{{{\rm{d}}\Re }}{{{\rm{d}}x}} = \frac{1}{2}{\Im ^2}\frac{{{\rm{d}}\wp }}{{{\rm{d}}x}} = \frac{1}{2}{i^2}\frac{{{\rm{d}}L}}{{{\rm{d}}x}} \quad [6]](/mediawiki/images/math/b/2/f/b2fd669547c840cf3fd1e48362377424.png)
Le espressioni ci dicono che la forza magnetica agisce nel senso di una diminuzione della riluttanza, di un aumento della permeanza o dell'induttanza.
Osservazione: Nel caso di campo lineare si può applicare la [5] con l'energia al posto della coenergia, cioè esprimere l'energia in funzione della variabile x e della forza magnetomotrice, quindi scrivere:
![f = \frac{{\partial {W_{campo}}}}{{\partial x}}(\Im ,x) \quad [7]](/mediawiki/images/math/5/e/3/5e311086b38fb7f0688df5424bee0e74.png)
Riepilogando
La forza magnetica agisce nel senso di determinare:
- una diminuzione dell'energia a flusso costante;
- un aumento della coenergia a f.m.m. costante (ed anche un aumento dell'energia se tra flusso e fmm esiste una relazione di proporzionalità);
- una diminuzione della riluttanza;
- un aumento della permeanza;un aumento dell'induttanza.
Esercizi
Esempio puramente teorico
Supponiamo che il legame tra forza magnetomotrice e flusso sia dipendente da x secondo una legge del tipo

Determiniamo l'espressione dell'energia del campo in funzione flusso del punto di lavoro (Ni * ,Φ * ) e di x con

Si ha

Se ci riferiamo alla coenergia dobbiamo considerare la funzione inversa

Calcoliamo la coienergia in corrispondenza al punto di lavoro NI *

Si ha


Forza di attrazione di un magnete
Calcoliamo la forza di attrazione agente tra due facce parallele di materiale ferromagnetico con flusso completamente perpendicolare ad entrambe (Nord: superficie da cui il flusso esce; Sud: superficie in cui il flusso entra) si può procedere come segue.
Sia g(x) = x la distanza in aria che separa le facce ed A l'area di ciascuna faccia, B il valore dell'induzione uniforme nel traferro che separa le facce.
L'asse di riferimento è parallelo all'induzione, l'origine è sulla faccia di sinistra.
La riluttanza del traferro è data da  .
.
Allontanando la faccia di destra, la riluttanza aumenta.
La forza magnetica agisce, come detto, nel senso di una diminuzione della riluttanza.
Applicando dunque la prima delle [6] si ha:
 .
.
Il segno - indica che f(x) è opposta al verso positivo assunto per l'ascissa x, quindi è di attrazione tra le due facce
Applicando la seconda delle [6]



Applicando la terza delle [6]



La forza tra le due superfici parallele è dunque di attrazione e vale

Dipende, in sostanza, dall'energia specifica immagazzinata e dalla superficie delle facce.
Determinazione della coppia
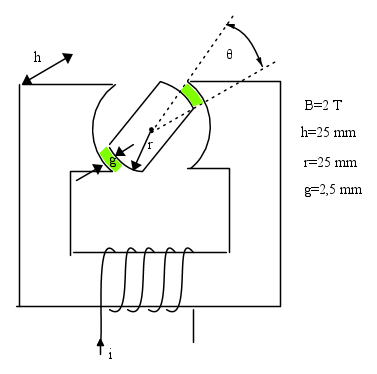
Immaginiamo un circuito magnetico come in figura, dove c'è una parte fissa (statore), su cui sta l'avvolgimento di eccitazione, che forma uno spazio cilindrico entro cui può ruotare un cilindro sezionato longitudinalmente in zone diametralmente opposte (il rotore), che completa il circuito magnetico. La rotazione può avvenire per lo spazio in aria (traferro) esistente tra statore e rotore.
Immaginiamo che il rotore nella posizione di figura, con le facce sezionate non orizzontali. Il flusso magnetico prodotto dall'avvolgimento passa nelle zone colorate in verde, con effetti di bordo che trascureremo.
Per calcolare la coppia agente sul rotore, determiniamo innanzitutto l'energia immagazzinata nel campo magnetico, ipotizzando che questo sia confinato nelle regioni colorate in verde.
Il volume di ciascun traferro si determina moltiplicando il suo spessore g per l'area A corrispondente al raggio medio, rm. Tale area è il prodotto della lunghezza dell'arco della circonferenza media il cui angolo al centro è indicato con θ. Quindi

L'energia magnetica immagazzinata nei due traferri ha l'espressione

Ora avendo considerato il sistema lineare, possiamo applicare la [7] essendo θ la variabile rispetto a cui derivare. Si ha allora

Postfazione
I concetti qui espressi si possono trovare anche nell'articolo citato nei riferimenti.
(Me lo ero completamente dimenticato :( )
Naturalmente leggere l'originale, cioè il libro della bibliografia, è quello che consiglio per una maggiore completezza.
Ad ogni modo questi erano gli "appunti" di oltre una decina di anni fa, che ora ho rivisitato, proponendoli agli eventuali studenti che dovessero passare di qui, nella speranza che possano risultare utili.
Bibliografia
- "Macchine Elettriche" -Fitzgerald-Kingsley-Kusko - E. Franco Angeli
Riferimenti
PS:
Ah, mi ero dimenticato anche di questo, sullo stesso argomento, più o meno, e un esercizio con FEMM perfino! :-)
(Beh, in fondo son passati 10 anni... :-( )

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)