Indice |
Generalità sull'interruzione di una corrente
Interrompere una corrente continua è più difficile che interromperne una alternata.
L'interruzione infatti richiede lo spegnimento dell'arco elettrico che inevitabilmente si forma tra i contatti non appena questi si allontanano. L'arco è una conseguenza della ionizzazione del gas isolante che li separa, generalmente l'aria, che produce cariche positive e negative per rottura di legami molecolari. Ciò avviene quando il campo elettrico generato dalla tensione tra i contatti, supera la rigidità dielettrica del gas.
L'insieme di ioni ed elettroni che ne deriva, forma il plasma che facilita il passaggio della corrente.
L'arco sviluppa calore che favorisce la ionizzazione. Per il suo spegnimento occorre sia ostacolare la ionizzazione asportando il calore sviluppato, sia rigenerare il gas, cioè deionizzarlo, per ristabilire le sue proprietà dielettriche. La deionizzazione è la ricombinazione delle cariche negative e positive del plasma ed è un fenomeno rapido, facilitato quando la corrente si annulla. In alternata la condizione favorevole alla rigenerazione, si presenta con una frequenza doppia di quella della corrente; in continua invece occorre realizzarla forzatamente. Per tale motivo, in alternata, l'interruzione è più agevole.
Nota
- Questo è anche uno dei vantaggi della corrente alternata per la realizzazione di interruttori adatti alle reti trasmissione e distribuzione di grandi potenze elettriche in alta tensione. La corrente continua avrebbe però molti altri vantaggi. Una discussione in proposito c'è in questo articolo di alcuni anni fa. Recentemente comunque ABB ha annunciato la realizzazione di un interruttore adatto ai sistemi HVDC il che dovrebbe cambiare notevolmente lo sviluppo futuro delle reti di potenza.
In questo articolo esamineremo l'interruzione di una corrente continua per individuarne i principali parametri che la caratterizzano.
Apertura di un circuito in continua
Ad interruttore chiuso la corrente nel circuito vale

in quanto l'induttanza, come è noto, è un cortocircuito in continua, quindi uL = 0 e l'interruttore, considerato ideale, pure. La KVL è allora E − RI = 0, da cui il valore di I0.
All'apertura si forma, tra i contatti dell'interruttore, l'arco elettrico, ai cui capi c'è una tensione ua, mentre la corrente varia, per cui l'induttanza entra in gioco con la tensione

La KVL è dunque

Il problema di questa equazione differenziale è l'espressione matematica da assumere per ua. Essa è infatti funzione della distanza tra i contatti e delle condizioni di temperatura e ionizzazione del gas, tutte fortemente variabili. Anche quando si è nelle condizioni finali di apertura, la caratteristica dinamica dipende dalla velocità con cui varia la corrente che determina la variazione di temperatura e ionizzazione. La seguente figura illustra come, a partire da una certa situazione, le caratteristiche dinamiche ua = f(I) che si hanno a seconda della derivata della corrente. Occorre fare alcune ipotesi semplificative per ricavare un modello matematico.
Un primo modello matematico
Un modello matematico approssimato, utilizzato nel dossier tecnico del primo link riportato nei riferimenti, considera l'arco come un generatore ideale di tensione, il che equivale ad assumere la curva c della precedente figura come caratteristica dinamica dell'arco.
All'apertura dei contatti si forma immediatamente l'arco, e la tensione ua inizia a crescere. Si suppone però che la corrente non vari fino all'istante in cui ua = E. E' questo l'istante zero dell'analisi che segue, ed è l'istante in cui si suppone che la tensione d'arco assuma il valore Ua che si manterrà costante. Ciò corrisponde ad applicare in quell'istante un gradino di tensione pari ad Ua, come mostrato nel seguente schema. Il gradino è un generatore ideale di tensione che cessa di essere tale non appena la corrente si annulla. Una ulteriore ipotesi è che il tempo che intercorre tra l'istante di apertura dei contatti e l'istante in cui la corrente comincia a variare, sia piccolo rispetto alla durata dell'arco , quindi rispetto alla costante di tempo del circuito che, come si vedrà, vi è strettamente legata.
All'istante apertura, che assumiamo come istante 0, per comodità e per le ipotesi fatte, la corrente vale

Dopo l'apertura l'equazione da considerare è, come già visto,

La soluzione è data da

con

con  costante di tempo
costante di tempo

Questa ultima equazione ci dice subito che se E > Ua ci sarà una corrente a regime permanente; quindi per avere l'interruzione, cioè per potere avere corrente nulla a regime, occorre che siaUa > E.
Per la continuità della corrente nell'induttore deve essere

quindi

quindi

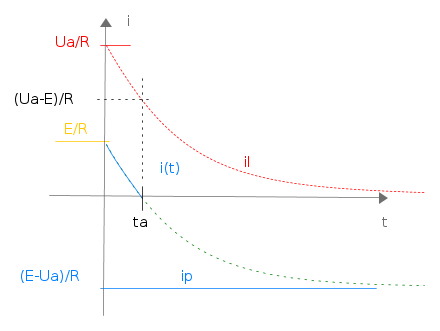
per cui per t > 0 si ha

L'istante ta in cui la corrente si annulla, avendo considerato t=0 l'istante iniziale, rappresenta il tempo di spegnimento e vale



L'energia sviluppata dall'arco è data da

Sviluppiamo i calcoli ed elaboriamo pazientemente la formula






![= \frac{{{U_a}\tau }}{R}E\left[ {\ln \frac{{{U_a}}}{{{U_a} - E}}\left( {1 - \frac{{{U_a}}}{E}} \right) + 1} \right] =](/mediawiki/images/math/0/7/3/073f767ebcbfc8c856b2081364e49885.png)
![= \frac{{{U_a}L}}{E}\frac{{{E^2}}}{{{R^2}}}\left[ {\ln \frac{{{U_a}}}{{{U_a} - E}}\left( {1 - \frac{{{U_a}}}{E}} \right) + 1} \right] =](/mediawiki/images/math/1/4/6/1467e19096b4c3dc14dea963a279cae9.png)
![= \frac{{{U_a}}}{E}LI_0^2\left[ {\ln \frac{{{U_a}}}{{{U_a} - E}}\left( {1 - \frac{{{U_a}}}{E}} \right) + 1} \right]](/mediawiki/images/math/1/d/6/1d66437647bd06455bb7309a8310baad.png)
Finalmente, posto  che è l'energia magnetica immagazzinata nell'induttanza all'istante iniziale, otteniamo
che è l'energia magnetica immagazzinata nell'induttanza all'istante iniziale, otteniamo
![W_a = 2{W_0}\frac{{{U_a}}}{E}\left[ {\ln \frac{{{U_a}}}{{{U_a} - E}}\left( {1 - \frac{{{U_a}}}{E}} \right) + 1} \right]](/mediawiki/images/math/1/d/2/1d297b6d6d34b1fd39559d972f9ed409.png)
Posto  sono di seguito tracciati i grafici di
sono di seguito tracciati i grafici di  e
e 
Secondo modello matematico
E' la trattazione seguita dal prof. Lorenzo Fellin nel testo riportato nel secondo link dei riferimenti.
Ipotizza una caratteristica dinamica dell'arco di tipo a (grafico del secondo paragrafo), assumendo che la corrente inizi a variare quando i contatti hanno raggiunto la posizione finale. Ciò presuppone che il tempo necessario a raggiungerla sia molto inferiore alla costante di tempo del circuito.
Ragionando sui grafici si possono ricavare espressioni del tempo di estinzione dell'arco e dell'energia da smaltire, che portano a valori sostanzialmente simili a quelli del precedente modello.
La forza elettromotrice di autoinduzione che si genera ai capi dell'induttanza per effetto della variazione di corrente è

Se tale tensione è costantemente negativa, il che significa che lo è la derivata della corrente, essendo l'induttanza L un numero positivo, la corrente diminuirà gradualmente dal valore iniziale I0 fino ad annullarsi.
In caso contrario assumerà un valore I1 inferiore ad I0, ma non nullo, in quanto a destra di I1 Δe è negativa, quindi la corente diminuisce; a sinistra di I1 è invece positiva quindi la corrente aumenta. In definitiva la corrente si stabilizza sul valore I1 e non si estingue.
Il permanere di questa situazione in genere determina il danneggiamento dei poli dell'interruttore.
Le due situazioni sono rappresentate rispettivamente nelle due figure seguenti.
figura 1
In questo caso la caratteristica d'arco è sempre superiore alla retta E − Ri. La tensione autoindotta nell'induttanza, è sempre in opposizione alla corrente per cui la corrente si estingue.
figura 2
Qui invece per correnti inferiori ad I1, la caratteristica d'arco è superiore alla retta E − Ri e la corrente si stabilizza su I1
Tempo di spegnimento
Dalla relazione

si ricava

cioè il tempo occorrente per la variazione di corrente Δi
Sommando tutti gli intervalli di tempo corrispondenti a tutte le variazioni che la corrente subisce per annullarssi, quindi per passare dal valore iniziale I0 a zero, si ricava il tempo di spegnimento (o durata dell'arco ta, che può essere calcolato con l'integrale

Per ottenere lo spegnimento che, come detto, si ha solo se si realizzano le condizioni illustrate nella figura 1, possiamo, in via semplificata, supporre che Δe sia costante e negativa, quindi porre Δe = − kE con k > 0
La caratteristica d'arco è perciò rettilinea come rappresentato in figura

Il tempo di spegnimento è in tal modo messo in relazione con la costante di tempo  del circuito.
del circuito.

Energia d'arco
Essendo
ua = E − Ri − Δe
quindi, assumendo l'ipotesi già fatta in precedenza
ua = E − Ri + kE
l'energia d'arco vale





Posto sempre  l'energia magnetica iniziale, si ha
l'energia magnetica iniziale, si ha

Nei grafici che seguono è riportato l'andamento del rapporto tra l'energia d'arco e l'energia immagazzinata nell'induttanza e del tempo di estinzione dell'arco con la costante di tempo del circuito in funzione del fattore k.
Parametri di un interruttore per corrente continua
Tensione massima e potere di interruzione: EM , IM
Le precedenti analisi matematiche mostrano che per ottenere lo spegnimento di una corrente continua, occorre che la caratteristica d'arco stabilita dall'interruttore, quando i suoi contatti hanno raggiunto la posizione finale, deve presentare una tensione sempre superiore alla tensione di alimentazione del generatore, diminuita della caduta dovuta alla corrente sulla resistenza in serie; in altre parole, la caratteristica d'arco non deve intersecare mai la retta E − Ri.
Ciò definisce una tensione massima di alimentazione EM, nonché una corrente massima  , quest'ultima detta potere di interruzione dell'interruttore.
, quest'ultima detta potere di interruzione dell'interruttore.
Costante di tempo massima ed induttanza limite: τM , LM
Nelle considerazioni precedenti si è ipotizzato un tempo di apertura dei contatti molto inferiore alla costante di tempo del circuito. A quest'ultima sono legati il tempo di estinzione dell'arco e l'energia da esso sviluppata che l'interruttore deve smaltire.
La minima energia d'arco è quella magnetica immagazzinata nell'induttanza, ma tale valore minimo si può ottenere solo con una durata dell'arco molto inferiore alla costante di tempo del circuito con conseguente aumento della potenza dell'arco.
Con tempi di spegnimento dell'ordine della costante di tempo  l'energia da smaltire è, come si può vedere dai grafici dell'ordine del 30% maggiore dell'energia minima W0.
l'energia da smaltire è, come si può vedere dai grafici dell'ordine del 30% maggiore dell'energia minima W0.
Con riferimento al primo modello un buon compromesso è fare in modo che sia
 il che comporta un'energia d'arco compresa nell'intervallo
il che comporta un'energia d'arco compresa nell'intervallo
1,17W0 < Wa < 1,3W0 ed un tempo di spegnimento compreso nell'intervallo 0,5τ < ta < τ
Con riferimento al secondo si trovano valori simili. Ad un tempo di apertura compreso nell'intervallo precedente, che corrisponde ad un valore della costante k nell'intervallo 1 < k < 2, l'energia da smaltire è compresa tra limiti simili ai precedenti.
Per ogni interruttore dunque esiste dunque una costante di tempo del circuito massima τM , quindi anche un'induttanza massima del circuito 
Le correnti che l'interruttore deve interrompere, oltre a quelle di normale funzionamento, quindi del valore della nominale od inferiore, sono le correnti di sovraccarico e di cortocircuito. Queste ultime sono le più gravose e lo sono tanto più quanto più vicino ai terminali dell'interruttore è il guasto che le determina.
In tale situazione, oltre alla elevata corrente il cui valore massimo deve essere inferiore al potere di interruzione, si ha un aumento della costante di tempo del circuito, e la retta E − Ri potrebbe intersecare la caratteristica d'arco impedendo lo spegnimento. Le norme specificano la costante di tempo a cui deve essere riferito il potere di interruzione degli interruttori in continua. Deve essere 
| Icn ( kA) | τcn(ms) |
|---|---|

| 5 |

| 5 |

| 5 |

| 5 |

| 10 |

| 15 |
| 50 < Icn | 15 |
E' in generale consigliabile prevedere in serie all'interruttore fusibili atti ad intervenire in caso di tale cortocircuito.
Per entrare nei dettagli dei vari parametri che caratterizzano un interruttore, occorre riferirsi alla Norma CEI 17.5
La figura seguente rappresenta qualitativamente l'andamento di tensione d'arco e corrente durante l'interruzione di un cortocircuito.
La corrente i assumerebbe il valore Icn secondo la costante di tempo del circuito, (indicata con T). All'istante ti i contatti cominciano ad allontanarsi. Si forma l'arco e la sua tensione ua cresce. Pochissimo dopo, all'istante t0, la corrente cessa di crescere ed inizia a calare, per effetto della tensione d'arco che raggiunge nelle rapide oscillazioni un valore massimo Ua con i contatti in posizione finale. All'istante tf la corrente si annulla e l'arco si spegne. Tra i contatti dell'interruttore si ha la tensione nominale di alimentazione. La durata dell'arco è ta = tf − t0

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)