Cos'è ElectroYou | Login Iscriviti

ElectroYou - la comunità dei professionisti del mondo elettrico

17
voti

Modellizzazione di un magnete permanente

Indice

Premessa

Come ha osservato RenzoDF nel suo articolo Magneti Permanenti -1, l'argomento è poco trattato nei tradizionali testi di Elettrotecnica.
Il recente commento ad un articolo sull'analogia tra circuiti elettrici e circuiti magnetici, mi ha indotto ad ampliare quella trattazione.

Magnete Permanente

il magnete permanente si ottiene sottoponendo ad opportuno campo magnetico un materiale ferromagnetico con ciclo di isteresi molto ampio, caratterizzato da una notevole induzione residua e da una elevata forza coercitiva.
Una volta realizzato, il magnete si troverà in un certo ambiente, nel quale svilupperà il campo magnetico dipendente dalle caratteristiche dell'ambiente.
Il magnete può essere "isolato" cioè lontano da altri materiali magnetici, ma, generalmente, l'ambiente che interessa è quello che gli si crea appositamente attorno con materiali magnetici: il circuito magnetico, un percorso prefissato per i flussi magnetici.

Prefissato nei limiti del possibile però, in quanto non un isolante magnetico, corrispondente agli isolanti elettrici. E' perciò molto più difficile, praticamente impossibile, definire con estrema precisione il circuito.
Nel circuito magnetico il magnete permanente è un componente attivo. Lo possiamo vedere come un generatore reale di flusso magnetico, corrispondente ad un generatore di corrente reale, o, dualmente, ad un generatore di tensione reale magnetica, corrispondente ad un generatore reale di tensione elettrica.
A seconda del circuito magnetico in cui è inserito induzione e campo del magnete si modificano, assumendo i valori che corrispondono a punti della sua caratteristica di smagnetizzazione.
Di seguito riporto, per comodità, le figure del citato articolo di RenzoDF:

Ciclo di isteresi

Ciclo di isteresi

Caratteristiche di smagnetizzazione

Caratteristiche di smagnetizzazione

Modellizzazione

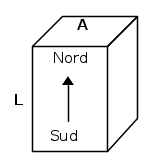
Consideriamo un magnete al Neodimio-Ferro-Boro a forma di parallelepidedo, di lunghezza L e sezione A.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad


Come si può vedere dalle curve di smagnetizzazione (la 2, blu), esso ha una caratteristica lineare.
Indicato con B0 il magnetismo residuo, con H0 il valore assoluto della forza coercitiva, nel secondo quadrante
\begin{array}{l} 0 \le B \le B_0 \\ - H_0 \le H \le 0 \\ \end{array}
si può scrivere

B=B_0+ \mu_P \cdot H

oppure

H=\frac {B_0}{\mu_p}-H_0

avendo posto
\mu_p=\frac {B_0}{H_0}
detta permeabilità reversibile del magnete.
Se il campo interno al magnete è uniforme, possiamo porre
\Phi=A \cdot B
uguale al flusso che lo attraversa e
\Im = -H \cdot L pari alla tensione magnetica, positiva, esistente tra il polo Nord, da cui esce il flusso, ed il polo Sud.
In pratica consideriamo il magnete come un generatore di flusso magnetico ed assumiamo per il segno di flusso e tensione magnetica, la convenzione dei generatori elettrici per tensione ed intensità di corrente: quindi flusso uscente dal punto a potenziale magnetico più alto, il Nord.
Avremo allora

\Phi=\Phi_0-\Lambda _P \cdot \Im

oppure

\Im = \Im _0 - \Re _P \cdot \Phi

dove

\begin{array}{l} \Lambda _P = \mu _P \cdot \frac{A}{L} \\ \Re_P = \frac{1}{{\Lambda _P }} \\ \Phi _0 = A \cdot B_0 \\ \Im _0 = H_0 \cdot L \\ \end{array}

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad


Limiti del modello

La modellizzazione è valida se il campo interno al magnete è uniforme. L'ipotesi di uniformità è verificata maggiormente quanto minore è la lunghezza del magnete, e si può verificare soprattutto quando il magnete è inserito in un ambiente o fa parte di un circuito ad alta permeabilità magnetica come mostrano le figure seguenti, relative ad un MP al NdFeB di dimensione 20 mm x 30 mm x 30 mm.

1-MP immerso in materiale magnetico ad alta permeabilità

1-MP immerso in materiale magnetico ad alta permeabilità

1a-Induzione in sezione centrale

1a-Induzione in sezione centrale

1b-Induzione sulla superficie del polo nord

1b-Induzione sulla superficie del polo nord

2-MP immerso in aria

2-MP immerso in aria

2a-Induzione in sezione centrale

2a-Induzione in sezione centrale

2b-Induzione sulla superficie del polo Nord

2b-Induzione sulla superficie del polo Nord

Oltre alla disuniformità nel campo si noti come nel caso del MP in aria si abbassino sensibilmente i valori di induzione per l'azione del campo smagnetizzante che, nel caso della prima figura è praticamente nullo. La prima figura corrisponde alla condizione di cortocircuito; la seconda al circuito "aperto" magneticamente.

Nota: per tutte le corrispondenze tra grandezze elettriche e magnetiche si faccia riferimento alla Tabella dell'articolo citato in premessa.

Osservazione

Il prodotto di tensione elettrica per intensità di corrente è una potenza elettrica, il che sta a significare che, ad esempio, da un generatore elettrico funzionante esce continuamente energia, energia che entra nel generatore dall'esterno. Il flusso di energia uscente dal generatore elettrico può continuare finché permane la fonte primaria di energia che fa funzionare il generatore.Il prodotto di flusso {\rm{Wb}}= {\rm{V}} \cdot {\rm{s}} per tensione magnetica A ha invece le dimensioni di un'energia, non di una potenza. E' legato all'energia complessiva immagazzinata nell'ambiente in cui è inserito il magnete permanente. Movimenti meccanici di parti del circuito magnetico ne alterano l'energia magnetica. Se diminuisce, è il campo magnetico a produrre il lavoro corrispondente ma, evidentemente, è una diminuzione che non può procedere all'infinito. Necessariamente per poter estrarre energia dal campo magnetico, occorre ripristinarla dall'esterno eseguendo lavoro sugli organi mobili, contro le forze del campo. Quindi tutti i marchingeni che girano in internet basati solo su MP e che promettono energia senza limiti ricavata dai magneti permanenti sono degli imbrogli.
L'analogia circuiti elettrici- circuiti magnetici presenta dunque a questo riguardo una differenza notevole: mentre il circuito elettrico è legato ad un flusso di energia che lo attraversa, il circuito magnetico rappresenta uno stato energetico.

Esercizio

Sia dato il seguente circuito magnetico con magneti permanenti.


Le dimensioni sono in millimetri. La profondità è di 30 mm.
Tra i magneti ed i gioghi esiste un traferro l_{t0}=0,1 \, {\rm{mm}}.
I magneti permanenti sono al Neodimio-Ferro-Boro.
L'induzione residua è
B_0=1,15 \, {\rm{T}}, la forza coercitiva H_0=883 \frac {{\rm{kA}}}{{\rm{m}}}
I magneti permanenti sono schematizzabili come generatori
\Phi_0=B_0 \cdot A = 1,15 \times 20 \times 10^{-3} \times 30 \times 10^{-3}=6,9 \times 10^{-4} \, {\rm{Wb}}
\Lambda_P= \mu_P \cdot \frac A L = \frac {B_0}{H_0} \cdot \frac A L=\frac {1,15}{883 \times 10^3} \times \frac {20 \times 30 \times 10^{-6}}{30 \times 10^{-3}}= =2,6 \times 10^{-8} \, {\rm{H}}
\Re _P = \frac{1}{{\Lambda _P }} = \frac{{10^8 }}{{2,6}} = 3,84 \times 10^7 {\rm{ H}}^{{\rm{ - 1}}}

Le riluttanze

Le riluttanze magnetiche dei gioghi e delle colonne sono trascurate e si considera solo la riluttanza dei traferri.
L'ampiezza totale dei due traferri che separano gioghi da una colonna è l_{t}= 2 \, {\rm{mm}}
Rs1 = Rd1
R_{d1}= \frac {1}{\mu_0} \cdot \frac {l_t}{S_t}=2 \times \frac {10^6}{1,256} \times \frac {10^{-3}}{20 \times 30 \times 10^{-6}}=2,65 \times 10^{6} \, {\rm{H^{-1}}}
Quella dei traferri che separano ciascun magnete dai gioghi vale:
R_{s0}=R_{d0}= \frac {1}{\mu_0} \cdot \frac {l_{t0}}{S_t}=0,2 \times \frac {10^6}{1,256} \times \frac {10^{-3}}{20 \times 30 \times 10^{-6}}= =0,265 \times 10^{6} \, {\rm{H^{-1}}}
Occorre poi tenere conto del flusso in aria tra i gioghi. Ricordiamo che non esiste un isolante magnetico. La riluttanza complessiva in aria tra i gioghi è data da
\Re_{gg}=\frac {L}{\mu_0 \cdot (A_g-2 \cdot A)}
\Re _{gg} = \frac{{10^6 }}{{1,256}} \times \frac{{30 \times 10^{ - 3} }}{{\left( {154 - 2 \times 20} \right) \times 30 \times 10^{ - 6} }} = 6,98 \times 10^6 \, {\rm{ H}}^{{\rm{ - 1}}}

Essa è l'equivalente di due riluttanze uguali
\Re _{gs} = \Re _{gd} = 2 \cdot \Re _{gg} \cong 14 \times 10^6 \, {\rm{ H}}^{{\rm{ - 1}}}

Osservazioni. I calcoli sono approssimati. La sezione effettiva del traferro è in generale maggiore di quella del ferro. Di quanto, dipende dall'ampiezza del traferro e dalla forma delle superfici affacciate. Si può ritenere trascurabile l'errore sulla riluttanza Rd0, un po' meno quello su Rd1, abbastanza meno su Rgd.

Ad ogni modo posto
R_0=\frac 1 {\Lambda_P}
I0 = Φ0
ed indicate con R le riluttanze ed i flussi con I ecco

Il circuito elettrico equivalente

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Il circuito è simmetrico rispetto all'asse AB. Si può allora considerare solo una delle due parti, immaginando di tagliare a metà il circuito, dove la corrente-flusso I è nulla.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

I_d = I_{0d} \cdot \frac{R_{gs}}{R_{gs}+R_{d1}}
R_{AB=}\frac{{R_{gs} \cdot R_{d1} }}{{R_{gs} + R_{d1} }} = \frac{{14 \times 2,65}}{{14 + 2,65}} \times 10^6 = 2,23 \times 10^6 \, {\rm{ H}}^{{\rm{ - 1}}}
R_{AC} = R_{AB} + R_{d0} = \left( {2,23 + 0,265} \right) \times 10^6 = 2,5 \times 10^6 \, {\rm{ H}}^{{\rm{ - 1}}}
I_{0d} = I_0 \times \frac{{R_0 }}{{R_0 + R_{AC} }} = 6,9 \times 10^{ - 4} \frac{{38,4}}{{40,7}} = 6,48 \cdot 10^{ - 4} \, {\rm{ Wb}}
I_d = \frac{{14}}{{16,65}} \times 6,48 \times 10^{ - 4} = 5,45 \times 10^{ - 4} \, {\rm{ Wb}}
Questo è il valore del flusso, Φd, che attraversa il traferro che separa il giogo dalla colonna.

Induzione al traferro

Ci interessa ad esempio conoscere il valore dell'induzione nel traferro. Qui occorre conoscere l'effettiva sezione di passaggio in aria, generalmente maggiore della sezione di ferro, tanto più quanto maggiore è lo spessore del traferro. Qui poi alterata probabilmente dalla maggior lunghezza delle colonne rispetto alla distanza tra i gioghi.
Ipotizzando un allargamento del 10%, avremo nel traferro un'induzione media di
B_t = \frac{{\Phi _d }}{{1,1 \cdot S_t }} = \frac{5,45 \times 10^{ - 4}}{{1,1 \times 20 \times 30 \times 10^{ - 6} }} = 0,826 \, {\rm{ T}}

Punto di lavoro del magnete

La tensione magnetica ai capi del magnete vale
U_P = U_{AC} = I_{0d} \cdot R_{AC}=6,48 \times 10^{-4} \times 2,5 \times 10^6=1620 \, {\rm{A}}
Il campo magnetico interno al magnete vale, in valore assoluto
\left| {H_P } \right| = \frac{{U_{AB} }}{{l_P }} = \frac{{1620}}{{0,03}} = 54000 \, \frac{{\rm{A}}}{{\rm{m}}}
La diminuzione di flusso dovuta alla permeanza del magnete è
I_{0d}^' = \frac{{U_{AB} }}{{R_0 }} = \frac{{1620}}{{38,4}}10^{ - 6} = 0,422 \times 10^{ - 4} {\rm{ Wb}}
Il flusso di lavoro del magnete è
I_{0d} = I_0 - I_{0d}' = (6,9 - 0,422) \times 10^{ - 4} = 6,48{\rm{ Wb}}
L'induzione di lavoro
B_P = \frac{{I_{0d} }}{A} = \frac{{6,48 \times 10^{ - 4} }}{{30 \times 20 \times 10^{ - 6} }} = 1,08{\rm{ T}}

Osservazione

è bene ricordare che i calcoli precedenti relativi alle grandezze puntuali, presuppongono una valore costante di queste nel volume considerato. Le cose in realtà sono più complesse ed i calcoli puntuali devono essere eseguiti con strumenti quali FEMM.

Verifica con FEMM

Ecco i risultai dei calcoli effettuati con [http://www.electroportal.net/admin/wiki/femmtutorial FEMM.
Nella seguente figura il valore dell'induzione (B=0,813 T) in un punto ed il grafico della stessa lungo il traferro.

Induzione nel traferro

Induzione nel traferro

Nella seguente i valore del campo (48364 A/m), dell'induzione (1,096 T) in un punto interno al magnete ed il calcolo della tensione magnetica (1494 A in valore assoluto).

Campo e tensione magnetica in MP

Campo e tensione magnetica in MP


I valori assomigliano abbastanza a quelli trovati con il circuito elettrico equivalente. La differenza è da attribuire all'approssimazione con cui sono calcolate le riluttanze. In particolare la riluttanza tra i gioghi è sicuramente inferiore al valore effettivo. Il che determina una derivazione del flusso prodotto maggiore ed un conseguente flusso minore verso il traferro giogo-colonna, con induzione minore. La minor riluttanza complessiva, vista di conseguenza dal magnete, determinerà una minore tensione magnetica ai suoi capi. I risultati di FEMM confermano tali considerazioni.

Nota 1: gli assi cartesiani sono quelli "soliti": asse delle ascisse x orientato a destra; asse delle ordinate, y, orientato verso l'alto. Il valore di Hy è negativo ed il calcolo di MMF è l' integrale di linea di H calcolato lungo un segmento parallelo e concorde all'asse y. La tensione magnetica ha segno opposto per la convenzione assunta dei generatori.
Nota2: le condizioni al contorno sono "Prescribed A", cioè con i coefficienti Ai tutti nulli, il che corrisponde a considerare tutto il campo magnetico confinato nel volume di calcolo di FEMM.

Riferimenti

"Modellistica dei sistemi elettromeccanici" - G. Superti Furga - 2003

Estratto da "https://www.electroyou.it/mediawiki/index.php?title=UsersPages:Admin:magnete-permanente"
7

Commenti e note

Inserisci un commento

di ,

wow è bello aver trovato un sito come questo, tempo fà quando trovavo nei risultati electroportal li scartavo sempre, perché ma sembrava un sito lasciato a se stesso...però ad oggi rimangio tutte le parole e, come dire, rignrazio questo articolo per avermi chiarito molte lacune sull'elettromagnetismo! grazie!

Rispondi

di ,

D'accordo Isidoro,la riluttanza non dissipa potenza; si intenda che l'analogia a volte aiuta a chiarire alcuni aspetti,(almeno nel mio caso... :( ..) a tal proposito ho trovato questo interessante articolo: http://www.electroportal.net/vis_resource.php?section=Lezio&id=116 ...... :) per metodi piu' complicati, presumo che ti riferisca a modelli matematici, vero?

Rispondi

di ,

Adminm, chiaro come al solito! Per mir: che l'analogia circuito elettrico/magnetico vada poco lontano lo si vede anche ad esempio dal fatto che la riluttanza viene rappresentata da una resistenza, ma la riluttanza non dissipa potenza! Ci sono altri modi di modellare i circuiti magnetici che non hanno di questi inconvenienti, ma sono parecchio piu` complicati.

Rispondi

di ,

Grazie per la risposta, chiara come sempre.Temo che dovrò rispolverare il sacro testo al capitolo : il campo magnetico-l'induzione elettromagnetica-materiali ferromagnetici-circuiti magnetici-

Rispondi

di ,

Il flusso energetico è rappresentato dalla potenza, non dalla corrente. La corrente è una componente della potenza elettrica. Nell'analogia, il flusso magnetico corrisponde all'intensità di corrente, quindi, se alla corrente vuoi associare il flusso di energia in transito nel circuito, la quale entra nel circuito attraverso il generatore, pone in movimento le cariche che l'acquisiscono trasferendola al carico, al flusso magnetico assocerai l'energia acquistata dallo spazio in cui esso esiste. Energia che permane cosi' com'è, se la causa che produce il flusso, o l'ambiente in cui il flusso si stabilisce, non si modificano. La corrente elettrica è costituita da particelle materiali in movimento lungo le linee di forza del campo elettrico; lungo le linee di forza che costituiscono il flusso magnetico, non c'è alcuna particella materiale in movimento (e neppure ferma). Il flusso magnetico rappresenta una proprietà che lo spazio acquisisce e mantiene e corrisponde ad un determinato quantitativo di energia; è una specie di deformazione dello stesso rispetto ad uno stato di riposo caratterizzato da assenza di energia. Puoi paragonarlo ad un corpo elastico che, in seguito ad una deformazione acquista energia; deformazione che il corpo mantiene finché non ne è rimossa la causa. Nello stato di deformazione non c'è un flusso di energia che attraversa il corpo elastico, ma c'è solo l'energia conseguente alla sua deformazione. E' la deformazione che rappresenta l'energia.

Rispondi

di ,

Interessante l'osservazione "Il prodotto di tensione elettrica ....." ed anche la differenza nell'analogia fra circuito elettrico e circuito magnetico; il flusso energetico che attraversa un circuito elettrico è rappresentato (se non erro) dall'intensità di corrente elettrica, mentre lo stato energetico del circuito magnetico ?

Rispondi

di ,

Non posso far ealtro che riconoscer ela mia ignoranza, anche in questo articolo. Non sapevo, ad esempio, che H0 fosse anche "forza coercitiva", come, non so nemmeno bene, cosa questa sia, a parte vaghe idee. Mi era tutto molto più chiaro quando la pensavo con intensità del campo magnetico.

Rispondi

Inserisci un commento

Per inserire commenti è necessario iscriversi ad ElectroYou. Se sei già iscritto, effettua il login.