Indice |
Introduzione
Il seguente articolo si propone di effettuare una breve panoramica degli impianti motori idraulici.
In principio erano le ruote idrauliche
Tra le macchine motrici più antiche, si ricordano sicuramente quelle idrauliche, che sono occorse all'uomo per sfruttare al meglio le energie che la natura aveva e metteva a sua disposizione.
Tra i "modelli" più elementari vi è senz'altro la ruota idraulica, sperimentata nelle sue forme più rudimentali per irrigare i terreni o per azionare delle piccole macine per cereali e furono sviluppate da Cinesi ed Egizi migliaia di anni fa.
Essa può essere messa in rotazione :
- sfruttando l'energia cinetica di un corso d'acqua, la cui corrente investe le pale inferiormente (immagine tratta da http://it.wikipedia.org/wiki/Ruota_idraulica) :
- impiegando il peso dell'acqua in delle apposite cassette, le quali vengono riempite nella parte superiore e svuotate poi in maniera graduale verso il basso per via della rotazione, come avviene nel caso della ruota idraulica a cassette (immagine tratta da http://web.tiscalinet.it/smsverdi/energia/ruotaidraulica.htm) :
Il loro limite consiste in :
- possibilità di impiego per piccoli salti;
- possibilità di impiego per portate limitate.
Le potenze impiegate corrispondono quindi a qualche kW o al più a qualche decina di kW.
Sono macchine ingombranti che funzionano con velocità di rotazione di certo non elevate, dell'ordine cioè dei pochi giri al minuto.
Per alcune di esse la costruzione è ancora di tipo artigianale.
/Le ruote idrauliche sono ancora oggi utilizzate laddove è possibile disporre di acqua di scarsa purezza e laddove l'affidamento della macchina debba essere dato a mani poco esperte, tenendo poco in considerazione il rendimento.
Le macchine idrauliche odierne sono le turbine che utilizzano l'energia cinetica che deriva dalla trasformazione di energia potenziale gravitazionale del fluido motore (che è sempre acqua) prima in energia di pressione e poi cinetica.
Inoltre l'applicazione delle turbine idrauliche è caratterizzata da accoppiamento diretto ad alternatori per la produzione di energia elettrica, senza l'impiego cioè di riduttori o moltiplicatori intermedi.
Le turbine ad azione (turbine Pelton)
Prima di entrare nella macchina il fluido possiede in sé un contenuto energetico notevole, che si esplica in energia di pressione.
Questo contenuto energetico può essere trasformato interamente o non interamente in energia cinetica nella parte fissa della turbina, mentre nel rotore si trasferisce energia meccanica all'esterno prelevandola solo dall'energia cinetica del fluido, se il contenuto energetico di cui si è detto prima viene trasformato interamente in energia cinetica, oppure la si preleva sia dall'energia cinetica sia da quella di pressione se tale contenuto energetico non è stato interamente convertito in energia cinetica.
Si parla quindi di turbina idraulica ad azione se il contenuto energetico viene convertito integralmente in energia cinetica nella parte fissa della macchina, cioè nello statore.
Si definisce inoltre il grado di reazione come il rapporto tra l'aliquota di energia convertita in energia cinetica e l'intero valore dell'energia stessa.
In sostanza, detta gH' l'energia potenziale gravitazionale di 1 chilogrammo di acqua e c1 la velocità di uscita dell'acqua dalla parte fissa della turbina, il grado di reazione R è pari a :

Viene da sé che per una turbina ad azione il grado di reazione R è pari a 0. Infatti in essa tutta l'energia potenziale gravitazionale si trasforma in energia cinetica nella parte fissa e quindi si ha che :

mentre se la trasformazione non è completa si ha un grado di reazione R > 0 con :

Una turbina idraulica ad azione, detta anche turbina Pelton dal nome dell'inventore Lester Allan Pelton, è formata da :
- una parte fissa o boccaglio, sagomato in maniera opportuna, da cui esce il fluido alla velocità
 ;
;
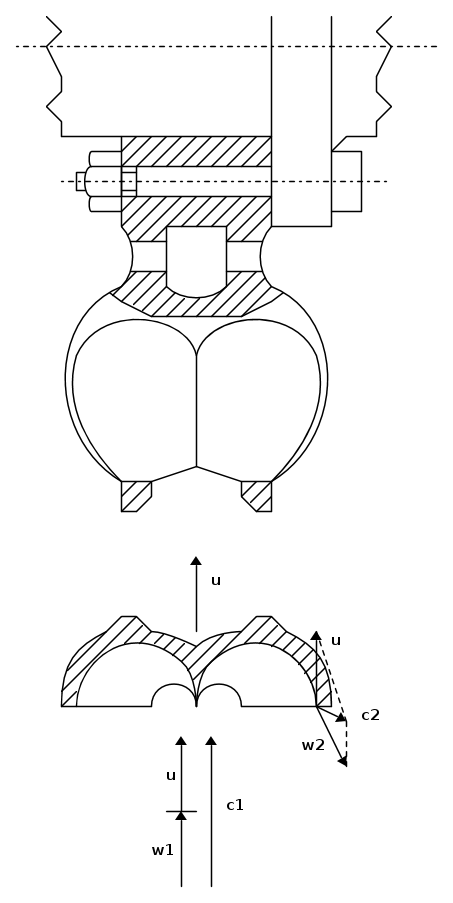
- una parte mobile, una ruota, formata da un disco portato da un albero munito dei relativi cuscinetti; alla periferia del disco sono sistemate le pale, quasi sempre fuse di pezzo con il disco, di forma particolare simile a quella di un doppio cucchiaio con uno spigolo tagliente al centro che consente di dividere il getto in modo simmetrico e che consente anche la ricaduta dell'acqua nel canale inferiore di scarico dopo un attraversamento fluidodinamicamente razionale.
Consideriamo la seguente figura, in cui è ritratta schematicamente la pala di ruota Pelton e i triangoli di velocità in ingresso ed in uscita :
Detta u la velocità periferica della ruota alla circonferenza dei getti e c1 la velocità assoluta del getto con direzione tangenziale alla ruota; u e c1 hanno quindi la stessa direzione.
Il triangolo di velocità all'ingresso si riduce ad un semplice segmento di retta dato che α1 = 0. La w1, che è a velocità relativa di ingresso, si ricava sottraendo la u alla c1. Se si trascurano gli attriti la velocità relativa di uscita w2 è pari alla w1 ed è diretta tangenzialmente al profilo del cucchiaio, nel bordo di uscita. La velocità assoluta di uscita, c2, si ottiene sommando u e w2.
L'acqua abbandona la ruota con una velocità c2 < c1 e quindi il lavoro meccanico trasferito all'esterno è uguale alla diminuzione di energia cinetica  che è subita dal fluido nella girante.
che è subita dal fluido nella girante.
Nel caso ideale il rendimento è :

Nel caso reale intervengono gli attriti e l'espressione del rendimento risulta molto più complessa.
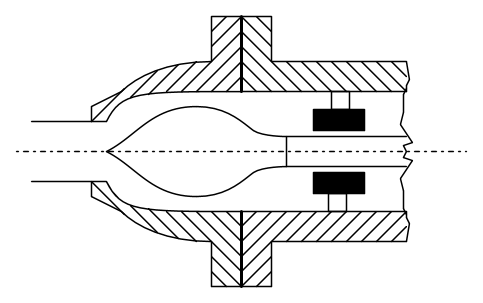
Nella figura che segue è rappresentato schematicamente il boccaglio della turbina Pelton, chiamato anche ugello Doble :
Esso è costituito da un condotto fortemente convergente nella parte finale, con al centro una spina otturatrice che scorre in direzione assiale grazie all'azione di un servomeccanismo e consente di aprire e chiudere l'ugello e di regolare la macchina.
Ad ogni posizione della spina corrisponde un diverso valore della sezione di efflusso Ω e quindi della portata volumetrica Q, che sarà pari a :

Dato che la  rimane praticamente inalterata, la variazione di sezione si esplica in una variazione di portata e quindi di potenza della turbina.
rimane praticamente inalterata, la variazione di sezione si esplica in una variazione di portata e quindi di potenza della turbina.
La spina fa sì che il getto sia molto compatto nel tratto tra la sezione di uscita e l'ingresso nella pala, con una distribuzione uniforme della velocità in tute le sezioni, dato che i filetti fluidi subiscono dei rallentamenti che sono praticamente uguali per la presenza all'esterno delle pareti del boccaglio e all'interno della spina.
Se la ruota è alimentata da un solo getto, il diametro d di quest'ultima è ricavabile dalla relazione :

da cui si ha :

Il diametro D della ruota dipende invece dalla velocità periferica della girante e si ricava dal rapporto u / c1 di massimo rendimento e dal numero di giri stabilito in base alla caratteristiche dell'alternatore dalla relazione :

dove :
- f è la frequenza;
- p il numero delle coppie di poli.
Inoltre per ogni diametro della ruota vi sono dei limiti riguardanti le dimensioni delle pale e dipendono dal diametro d del getto.
Nella pratica costruttiva il rapporto D / d è compreso tra 12 e 18 e non può andare al di sotto di 8. Occorre avere molta attenzione anche nello stabilire il numero delle pale, cioè il passo. Una pala, infatti, ruotando, taglia il getto mentre la parte di quest'ultimo a valle della pala stessa prosegue la sua traiettoria rettilinea.
Affinché tutta l'energia cinetica venga interamente sfruttata è necessario che l'ultimo filetto del getto tagliato raggiunga la pala successiva e la percorre tutta prima che essa esca fuori dalla traiettoria.
Comunque, quando si va a progettare una turbina Pelton è difficile rispettare tutte le condizioni finora citate e quindi è necessario frazionare la portata dividendola in due o più getti.
Le Pelton possono avere da 2 a 6 getti, disposti in maniera opportuna attorno alla girante. La seguente foto (tratta da http://www.cmr-hydro.it/prodotti-turbine-pelton2.htm) ritrae una spirale Pelton a 4 getti :
Le potenze erogate dalle turbine Pelton sono dell'ordine di decine di migliaia di kW (fino a 100 MW e anche oltre).
Le turbine a reazione
In turbine di questo tipo l'energia potenziale gravitazionale corrispondente al salto utile Hu si trasforma in energia cinetica in parte nello statore ed in parte nelle pale mobili della girante.
Quest'ultima è alimentata tramite acqua in pressione e solo al suo interno questa pressione decresce fino al valore della pressione atmosferica o anche a valori inferiori, se a valle della ruota e fino al canale di scarico è posizionato un condotto fisso sagomato in maniera opportuna, che è il tubo di aspirazione o diffusore.
Francis
La turbina idraulica a reazione più antica è la turbina Francis.
E' formata principalmente da una ruota munita di pale, detta girante, circondata da una corona di pale fisse che forma lo statore o distributore. Una voluta convoglia poi l'acqua nei condotti : essa ha una forma tipica a chiocciola e tale forma è funzione prevalentemente del valore della portata che attraversa le singole sezioni della stessa e che decresce a mano a mano che l'acqua fluisce verso la parte interna della turbina.
La seguente figura, tratta da http://www.salesianischio.it/cfp/lavori/energiaingioco/it/Produzione/turbina_francis.html, ritrae la girante di una turbina Francis :
Questa invece (tratta da http://www.cmr-hydro.it/prodotti-turbine-francis3.htm), ritrae il distributore di una turbina Francis :
Un esempio di voluta a chiocciola di turbina Francis e distributore ci è dato, invece, dalla seguente figura (tratta da http://www.cmr-hydro.it/prodotti-turbine-francis1.htm) :
Il distributore è formato da una serie di pale direttrici d che delimitano condotti a sezione decrescente in modo tale da favorire l'aumento della velocità c1 dell'acqua che in tal caso, dato che il grado di reazione R è diverso da zero, è data da :

Nella ruota si riscontrano anche un disco, una corona esterna, le pale che si incurvano avvicinandosi tra loro dall'entrata all'uscita e delimitano anch'esse dei condotti a sezione decrescente dato che, trattandosi di turbina a reazione, ci deve essere un aumento della velocità relativa (w2 > w1) e una diminuzione di pressione anche nella girante.
Sia la velocità relativa di ingresso w1 nelle pale, sia quella assoluta di uscita c2 sono dirette verso l'asse a cui si avvicina il getto liquido nel suo percorso.
La turbina Francis è quindi una macchina centripeta.
Il massimo rendimento si ha per valori nulli della componente tangenziale della c2 della c2 di uscita, ma i rapporti u1 / c1 variano in un intervallo più esteso rispetto a quello delle turbine Pelton. Tale rapporto può andare da 0,45-0,50 fino a 0,90 ed oltre ed è influenzato in maniera considerevole dagli angoli (α1 e β1) che la velocità assoluta c1 in ingresso alla girante e quella relativa w1 formano con la velocità periferica u1.
Per regolare la potenza della turbina Francis, si ricorre alla variazione della portata grazie alla modifica simultanea dell'orientamento della pale d del distributore che possono ruotare su perni appositi durante i transitori.
Le turbine Francis sono adoperate per salti geodetici che variano da qualche decina di metri fino 300-400 m, con portate anche molto elevate.
Assiale ad elica e Kaplan
L'evoluzione della pala della turbina Francis porta ad una girante assiale, simile ad una elica di propulsione. Si arriva alla turbina ad elica, in cui dopo il distributore (centripeto) il fluido è soggetto ad una deviazione di 90° nel condotto fisso prima di giungere alla girante formata da poche grandi pale, che sono fissate ad un mozzo di dimensioni notevoli, con un profilo piatto e che sono progettabili per mezzo della teoria aerodinamica, assegnando ai vettori delle velocità relative gli angoli di incidenza maggiormente idonei a realizzare il rendimento massimo.
Turbine di questo tipo riescono ad essere impiegate anche per salti geodetici piccoli con portate molto elevate, fino a 500 m3/s e con potenze di 300-500 MW .
Una evoluzione ulteriore di questa categoria di macchine conduce alle turbine Kaplan, dal nome del professore Viktor Kaplan. Esse sono dotate di un dispositivo posizionato nel mozzo che permette di variare l'inclinazione delle pale in riferimento alle variazioni del carico e in sincronismo con le pale del distributore.
Tubo di aspirazione o tubo diffusore
Nelle turbine con grado di reazione elevato, il salto geodetico utile può essere anche piccolo e in questo caso la perdita allo scarico dovuta alla velocità assoluta di uscita c2 può avere una incidenza dal punto di vista percentuale rilevante che porta poi ad una diminuzione del rendimento.
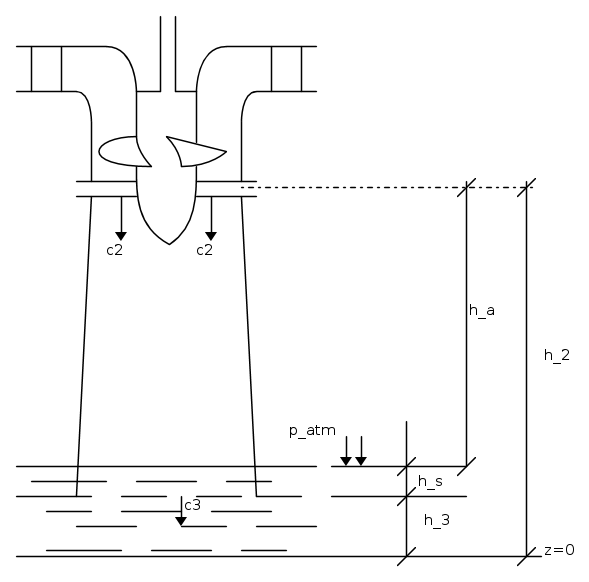
Si può ovviare all'inconveniente se si installa la turbina ad un livello superiore al canale di scarico e se si sistema all'uscita della macchina un tubo di aspirazione conico in cui il fluido viene rallentato (c3 < c2) e una parte dell'energia cinetica relativa alla velocità c2 di uscita si converte in energia di pressione.
Poiché nel canale di scarico si è alla pressione atmosferica, all'uscita della girante è necessario avere una pressione minore di quest'ultima e ciò porta ad un aumento virtuale del salto utile Hu.
La seguente figura ritrae schematicamente il tubo diffusore o di aspirazione :
Possiamo scrivere la equazione di Bernoulli tra le sezioni di ingresso ed uscita del tubo di aspirazione :

dove ξ rappresenta le perdite di carico che si hanno durante l'attraversamento del condotto.
Se hs è la distanza tra il pelo libero del canale di scarico e la sezione di uscita del tubo, l'altezza h3 del tubo è pari a :
e si ha anche :

Si ricava quindi anche l'altezza piezometrica nella sezione 2 di ingresso nel tubo :

Il termine sottrattivo dell'espressione precedente è il recupero ottenuto con il tubo di aspirazione conico che consiste in un aumento virtuale del salto utile Hu. Se il tubo fosse cilindrico il recupero sarebbe nullo ed in tal caso la depressione creata dal tubo aspirante compensa solo l'aumento dell'altezza geodetica con cui la turbina è sistemata rispetto al canale di scarico.
La depressione creata a valle della ruota ha comunque un limite perché vi è un minimo possibile per il termine p2 / γ dato che deve essere sempre rispettata la condizione :

dove i termini pv / γ e pa / γ sono le altezze piezometriche che corrispondono alla tensione di vapore alla temperatura dell'acqua e alla pressione parziale dell'aria disciolta.
Se non fosse rispettata la condizione prima citata si avrebbe il fenomeno della cavitazione con il liberarsi di bolle d'aria e di vapore che comporterebbe un funzionamento irregolare e rumoroso nonché l'usura dei materiali.
una volta stabilito il valore minimo di p2 / γ si può risalire all'altezza del tubo :

L'altezza in generale arriva a valori massimi di 7 m.
Bibliografia
Quanto esposto è tratto da :
- Macchine - Renato della Volpe :

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)