ElectroYou - la comunità dei professionisti del mondo elettrico

Vai a: navigazione, ricerca

In un recente post [1] MarcoD domandava quali fossero i criteri di dimensionamento del filtro LC di un convertitore Buck in una applicazione particolare. Mentre i normali convertitori a commutazione sono progettati per lavorare con tensione di ingresso variabile e devono mantenere la tensione di uscita fissa, anche con carico variabile, in questa applicazione con celle Peltier, la tensione di ingresso è costante, come pure il carico resistivo, ma si deve poter variare la tensione di uscita e di conseguenza la corrente sul carico.

Questo articoletto non è un vero rapporto di progetto ma sono semplicemente le note di "brutta copia" che normalmente scriverei sul retro di una busta (back-of-the-envelope calculations). Suppongo che chi legge sappia come funziona un Buck, per cui ci saranno solo brevi richiami alla teoria del circuito.

Introduzione

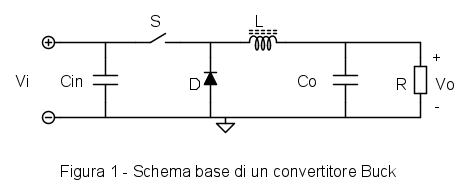
Uno dei convertitori più flessibili e versatili è il convertitore Buck o step-down, detto anche chopper. Questo convertitore ha svariate buone proprietà quali facilità di controllo e possibilità di utilizzo in un campo enorme di potenze, dalla frazione di watt alla decina di megawatt!

Nella sua implentazione più comune, Fig. 1, il circuito presenta un interruttore in posizione hi-side, quindi un pochino più complicato da pilotare rispetto a un interruttore riferito a ground.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

L'applicazione analizzata in questo articolo è l'alimentazione di celle Peltier per un sistema raffreddante. La differenza rispetto a un normale applicazione di un convertitore Buck è che questa applicazione ha il carico $R\,$ costante come pure la tensione di ingresso $V_{i}\,$ , mentre deve essere variata la tensione di uscita $V_{o}\,$ variando il duty cycle $D\,$ , e di conseguenza anche la corrente di uscita $I_{o}\,$ . La tensione di uscita deve poter essere variata fra zero e $V_{i}\,$ .

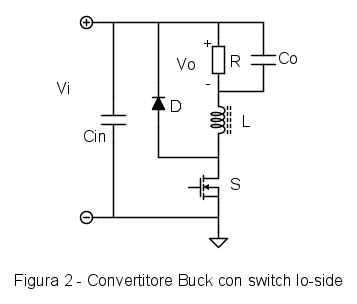
In questa applicazione il controllo viene fatto misurando la temperatura del sistema, che risponde con costanti di tempo enormemente più lunghe rispetto al periodo di commutazione, mentre non è richiesto avere una retroazione dalla tensione di uscita. Questo permette di modificare il circuito portando l'interruttore in posizione lo-side, come mostrato in Fig. 2.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Le proprietà di questo circuito sono esattamente quelle del Buck standard, anche perché è un Buck solo disegnato in un altro modo, ma presenta lo switch riferito a ground, quindi più facile da pilotare. Inoltre il carico è ancora collegato a un potenziale fisso, in questo caso il positivo dell'ingresso, quindi la tensione di modo comune sul carico è costante e non ci sono problemi di compatibilità elettromagnetica.

Equazioni di progetto

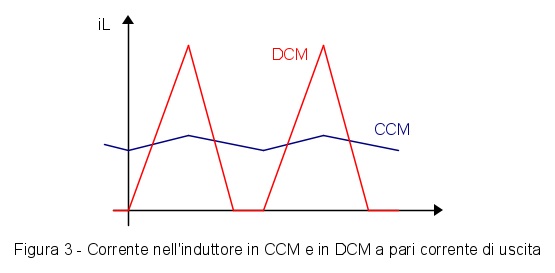
I convertitori a commutazione possono essere progettati per funzionare in modo continuo, CCM, in cui la corrente dell'induttore non va mai a zero e in modo discontinuo, DCM, in cui la corrente va a zero alla fine di ogni ciclo, come mostrato in Fig. 3.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

La differenza di comportamento fra i due modi è sostanziale. In DCM la corrente di picco è almeno doppia rispetto al funzionamento in CCM, inoltre in CCM il convertitore si comporta per se come una buona sorgente di tensione. In generale si cercherebbe di far lavorare un convertitore in CCM, ma in alcuni casi il legame dinamico fra tensione di uscita e duty cycle in CCM fa sì che il convertitore sia molto difficile o impossibile da controllare, per cui si è costretti a progettare il convertitore in DCM.

Nel caso del Buck si è fortunati, perché è facile controllarlo e addirittura in questo caso il controllo sulla tensione di uscita non è necessario perché anche staccando il carico la tensione di uscita non diverge, come invece capita con altre topologie.

Le equazioni di progetto permettono di calcolare il valore dell'induttanza e gli stress elettrici dei componenti, così da poterli selezionare in fase di progetto. Nel seguito si useranno le equazioni ricavate per componenti ideali. Nel caso di componenti reali le variazioni dei risultati sono sufficientemente piccole per cui non vale la pena di sviluppare equazioni più complicate e sostanzialmente poco utili. Si supporrà anche di lavorare a frequenza di commutazione costante $f_{sw}=1/T_{sw}\,$ , come capita nella grande maggioranza dei casi, e sempre quando il convertitore è controllato da un microcontrollore.

Le equazioni fondamentali in CCM, che non cambiano anche quando si lavora a tensione di ingresso fissa e tensione di ucita variabile sono il legame fra tensione di ingresso e uscita

$V_{o}=D V_{i} \qquad \qquad (1)$

in cui si vede che la tensione di uscita dipende linearmente dal duty cycle, e può variare da zero, con duty cycle nullo e quindi interruttore sempre aperto, a un valore pari alla tensione di ingresso quando il duty cycle è pari a uno, quindi interruttore costantemente chiuso.

La seconda equazione invariante è quella che definisce l'induttanza critica, cioè quel valore di induttanza che porta il convertitore a lavorare sul confine fra modo continuo e modo discontinuo

$L_{crit}=\frac{R(1-D)}{2 f_{sw}}\qquad \qquad (2)$

Per rimanere in modo continuo l'induttanza deve essere maggiore di quella critica nel caso più sfavorevole, come sarà mostrato nella prossima sezione.

La formula (2) è l'unica relazione che fornisce il valore di un componente, gli altri componenti vengono scelti in base agli stress elettrici che debbono sopportare o in base ai loro parametri parassiti. È quindi necessario trovare gli stress di tensione e corrente dei vari componenti. Per questo scopo bisogna trovare i valori di picco della corrente nell'induttore, riferendo questi valori alla tensione di ingresso (costante) e al duty cycle.

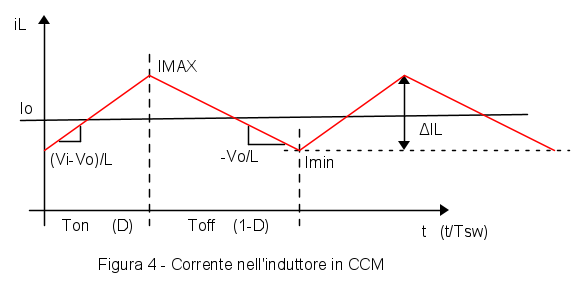
In Fig. 4 è rappresentata la corrente di induttore di un Buck in modo continuo, con la pendenza delle rampe di salita e discesa. La corrente di uscita $I_o\,$ è il valor medio della corrente nell'induttore.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

La pendenza delle correnti nell'induttore è valutata trascurando le resistenze parassite e le cadute sull'interruttore e sul diodo. Se si volessero includere anche le cadute di tensione sui semiconduttori, le due pendenze risulterebbero rispettivamente pari a $\frac{V_i-V_o-V_{sw}}{L}$ e $\frac{-V_D-V_o}{L}$ con l'effetto di ridurre la pendenza della salita e aumentare quello della discesa di corrente. L'effetto delle perdite è minuscolo e se si considerassero le formule risultanti sarebbero inutilmente complicate.

I valori di $I_{max}\,$ e $I_{min}\,$ vengono ricavati imponendo che la variazione di corrente in salita sia uguale a quella in discesa e uguale a $\Delta I_L\,$ e che la corrente media dell'onda triangolare sia pari alla corrente di uscita $I_o\,$ .

$\Delta I_L=I_{MAX}-I_{min}=\frac{(V_{i}-V_o)D}{f_{sw}L}=\frac{V_o(1-D)}{f_{sw}L}\qquad \qquad (3a)$

$I_o=\frac{V_o}{R}=\frac{I_{MAX}+I_{min}}{2} \qquad \qquad \qquad \qquad(3b)$

Risolvendo il sistema delle equazioni (3) e portando tutto in funzione di $V_{i}\,$ e $D\,$ si ottiene

$I_{MAX}=\frac{ V_i D}{R}+\frac{V_iD(1-D)}{2 f_{sw}L}\qquad \qquad (4a)$

$I_{min}=\frac{ V_i D }{R}-\frac{V_iD(1-D)}{2 f_{sw}L}\qquad \qquad (4b)$

e il ripple picco-picco della corrente nell'induttore vale

$\Delta I_L=\frac{V_iD(1-D)}{f_{sw}L} \qquad \qquad \quad (5)$

Le equazioni da (3) a (5) sono essenzialmente le relazioni diverse da quelle standard che devono essere usate per il progetto del Buck usato a tensione di uscita variabile.

Per calcolare lo stress sui componenti servono essenzialmente le correnti, in qualche caso il valore di picco, in altri quello medio e in altri ancora quello efficace. Si parte identificando le correnti che interessano, in particolare quella attraverso l'interruttore $I_{sw}\,$ , attraverso il diodo $I_{D}\,$ e i condensatori di ingresso $I_{Ci}\,$ e uscita $I_{Co}\,$ .

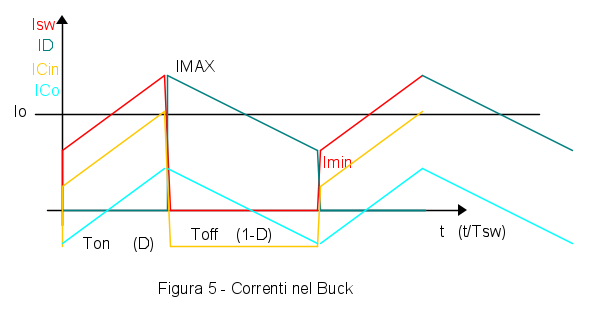
In Fig. 5 sono riportate le forme d'onda che servono, ricavate dalla corrente attraverso l'induttore.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

In particolare la corrente dell'interruttore (traccia rossa) è uguale a quella dell'induttore durante l'intervallo $T_{on}\,$ , oppure, se si usa il tempo normalizzato rispetto a $T_{sw}\,$ , bisogna considerare l'intervallo $D\,$ . La corrente attraverso il diodo (traccia blu) e` pari a quella dell'induttore durante la fase $T_{off}\,$ oppure $1-D\,$ . Le correnti attraverso i condensatori di ingresso e di uscita sono rispettivamente pari a quella dell'interruttore depurata del suo valore medio (traccia gialla), mentre nel condensatore di uscita la corrente e` quella dell'induttore depurata del suo valore medio (traccia azzurra).

Correnti

Le correnti importanti per il dimensionamento dipendono dal componente. Se il componente ha un comportamento resistivo (ad esempio il MOS) oppure ha una resistenza parassita (ad esempio l'induttore o le $ESR\,$ dei condensatori), lo stress è dato dalla corrente efficace poiché la potenza dissipata dipende dalla corrente efficace al quadrato. Invece se il componente ha un comportamento a tensione costante, ad esempio il diodo, si deve calcolare la corrente media, perché la potenza dissipata è appunto dato dal valor medio della corrente. Per calcolare i valori efficaci delle onde trapezioidali si utilizza la flat top approximation, che consiste nell'approssimare il trapezio con un rettangolo con la stessa area e poi si calcola il valore efficace del rettangolo, molto più rapido da calcolare di quello del trapezio. L'errore commesso e` minimo!

MOS

Il MOS in conduzione si comporta come una resistenza di valore $R_{sw}\,$ che dipende dalla $r_{DSon}\,$ e dalla temperatura.

Il valore efficace della forma d'onda rossa di Fig. 5, usando l'approssimazione di flat top, vale

$I_{swRMS}=I_o \sqrt{D}=\frac{V_i D\sqrt{D}}{R} \qquad \qquad (6)$

Il valore massimo di questa corrente si ha per $D=1\,$ , mentre il valore di picco è ovviamente $I_{MAX}\,$ .

Diodo

Per il diodo i valori importanti sono la corrente media e la corrente di picco. Il valore medio della corrente blu di Fig. 5 vale

$I_{Dave}=I_o(1-D)=\frac{V_i D(1-D)}{R}\qquad \qquad (7)$

e il suo valore massimo si ha per $D=0.5\,$ . mentre il valore di picco è di nuovo $I_{MAX}\,$

Induttore

La scelta dell'induttore richiede il valore della corrente di picco, legata alla saturazione del nucleo magnetico, e la corrente efficace per le perdite nel conduttore. Nei convertitori in CCM il ripple di corrente, che provoca potenza dissipata per perdite nel nucleo è praticamente ininfluente.

La corrente efficace nell'induttore si potrebbe calcolare con una formula abbastanza complicata, ma a tutti gli effetti può essere approssimata con la sua corrente media

$I_{LRMS}=\sqrt{I_o^2+\frac{\Delta I_L^2}{12}}=\sqrt{\left(\frac{V_iD}{R}\right)^2+\left(\frac{V_iD(1-D)}{f_{sw}L}\right)^2 \bigg / 12}\approx \frac{V_iD}{R}\qquad \qquad (8)$

La corrente di picco, ancora una volta, è pari a $I_{MAX}\,$

Condensatore di uscita

Le correnti da specificare per il condensatore di uscita sono il valore efficace della corrente attraverso il condensatore, traccia azzurra di Fig. 5, e il valore picco picco della corrente.

Il valore efficace di un'onda triangolare a valor medio nullo e di ampiezza $\Delta I\,$ vale

$I_{CoRMS}=\sqrt{\frac{\Delta I_L^2}{12}}=\frac{\Delta I_L}{\sqrt{12}}=\frac{V_iD(1-D)}{\sqrt{12}f_{sw}L}\qquad (9)$

L'ampiezza picco picco della corrente attraverso il condensatore di uscita è dato dall'equazione (5), cha ha la condizione di massimo per $D=0.5\,$

Condensatore di ingresso

Un aspetto importante da tenere presente nel progetto è che il condensatore di ingresso $C_{in}\,$ , essendo collegato direttamente all'interruttore $S\,$ è soggetto ad un elevato stress di corrente, mentre il condensatore di uscita, alimentato dall'induttore $L\,$ subisce uno stress molto minore.

La corrente efficace che attraversa il condensatore di ingresso sembrerebbe complicata da calcolarsi perché la forma d'onda non è standard. Ovviamente non si può usare la legge di Kirchhoff sul nodo di ingresso per le correnti efficaci, in quanto l'operatore RMS non è lineare. Si può per usare una variante della KCL, detta KCL quadratica che si applica ai valori efficaci. Applicata a questo caso si ha $I_{CinRMS}^2=I_{swRMS}^2-I_{inDC}^2$ da cui

$I_{CinRMS}=\sqrt{\frac{V_i^2 D^3}{R^2}-\frac{V_i^2 D^4}{R^2}}=\frac{V_iD}{R}\sqrt{D-D^2}=\frac{V_iD}{R}\sqrt{D(1-D)}\qquad (10)$

IL massimo di questa espressione si ha per $D=0.75\,$ Nel condensatore di ingresso il valore picco picco della corrente non è importante.

Tensioni

Per i semiconduttori e i condensatori sono importanti anche le tensioni massime che si trovano a sopportare. In questo caso non ci sono particolari problemi. Il condensatore di ingresso, il MOS e il diodo sono sempre sottoposti alla tensione di ingresso mentre il condensatore di uscita ha ai suoi capi una tensione varibile, che puo` arrivare al valore della tensione di ingresso. Quindi tutti i componenti devono essere dimensionati per sopportare almeno $V_{i}\,$ .

Progetto

Dopo aver ricavato l'equazione di progetto e quelle di stress dei componenti si può passare al dimensionamento del circuito che deve soddisfare i seguenti requisiti:

Tensione di ingresso costante pari a $V_i=50\,\text{V}$
Carico costante con valore $R=11.5\,\Omega$
Tensione di uscita variabile con il duty cycle $0\,V\le V_o \le V_i$ . La tensione nulla in uscita si ottiene tenendo continuamente spento il transistore, la tensione massima, quasi uguale a $V i$ la si ottiene tenendo acceso continuamente l'interruttore.
Ripple picco picco della tensione di uscita, supponiamo $1\,%$ della tensione di uscita massima, quindi $0.5\,\text{V}$ .

Il progetto di un Buck è praticamente sempre fatto in modo continuo, riducendo gli stress di corrente e avendo una tensione di uscita ad anello aperto ben regolata, di valore

$V_o=V_i\,D$

Come si vede dalle equazioni della sezione precedente, compare spesso il prodotto $f_{sw}L\,$ che impica che si può scegliere più o meno liberamente uno di questi due parametri e l'altro viene determinato di conseguenza. Di solito la scelta iniziale è sulla frequenza di commutazione, tenendo presente che maggiore è la frequenza minore è il valore dell'induttanza, ma con la frequenza crescono anche le perdite di commutazione.

Di solito la scelta è fatto a buon senso e in base all'esperienza, ma in questo caso esiste un vincolo ulteriore che è dato dal voler utilizzare un microcontrollore per la generazione del segnale di comando in PWM. Il microcontrollore in questione, ATMega328 può generare una frequenza massima di PWM pari a $f_{sw}=62.5\,\text{kHz}$ , un po' bassa per questi livelli di potenza, ma comunque non disprezzabile e sicuramente utilizzabile. Il contatore che genera il segnale PWM ha una larghezza di 8 bit, e riesce quindi a generare 256 diversi valori di durata dell'impulso, una risoluzione ampiamente sufficiente per il controllo delle Peltier.

Induttore

Il primo componente da dimensionare è l'induttore, poiché dal suo valore dipende il ripple di corrente e quindi gli stress di picco.

Avendo scelto la frequenza di commutazione, la sola equazione di progetto del Buck è la (2) che permette di calcolare il valore dell'induttore. Volendo lavorare in modo continuo bisogna mettersi nel caso in cui il valore di $L_{crit}\,$ è massimo e poi scegliere un valore $L>L_{crit}\,$ . Nella formula (2) entrano in gioco la resistenza di uscita, costante, la frequenza di commutazione, già scelta e il duty cycle, che può variare fra 0 e 1. Per massimizzare il valore di $L_{crit}\,$ si considera il caso di $D=0\,$

$L_{crit}=\frac{R(1-D)}{2f_{sw}}\qquad \Rightarrow \qquad \frac{R}{2f_{sw}}=\frac{11.5\Omega}{2\times 62.5\text{kHz}}=88\mu\text{H}$

Poiché l'induttanza effettiva deve essere maggiore di quella critica, la si sceglie di almeno $100\,\mu\text{H}$ . In realtà, considerando una tolleranza del $20\,%$ , bisognerebbe salire almeno a $120\,\mu\text{H}$ , ma in pratica non è necessario perché l'induttanza massima è richiesta con il duty cycle minimo, quindi con corrente di uscita minima. Gli induttori a bassa corrente hanno una induttanza pari o maggiore di quella dichiarata, quindi si rispetta comunque la specifica. Ad alta corrente l'induttanza diminuisce dal $20%\,$ fino al $40%\,$ circa, ma questo non porta il convertitore a lavorare in DCM perche' questa riduzione avviene quando la corrente di uscita è elevata.

D'ora in avanti il valore dell'induttanza nominale sarà di $100\,\mu\text{H}$ . Al più, se si volessero calcolare casi di worst case, la si può ridurre quando l'uscita è ad alta tensione e corrente.

Per selezionare l'induttore servono ancora la corrente massima e la corrente efficace. Analizzando la relazione (4a) che fornisce la corrente di picco si trova in questo caso specifico che la corrente di picco massima capita per $D=1\,$ (cosa che non capita in generale nei buck usati a tensione di uscita costante). Dalla eq. (4a) si vede che per D=1 la corrente massima è pari a quella di uscita.

$I_{max}=\frac{V_i}{R}=\frac{50\text{V}}{11.5\Omega}=4.4\,\text{A}$

La corrente efficace attraverso l'induttore è praticamente la corrente di uscita massima, che si ha con tensione di uscita massima applicata al carico.

In definitiva serve un induttore con induttanza di $100\,\mu\text{H}$ e corrente di lavoro di almeno $5\,\text{A}$ . Possibili componenti adatti per questa applicazione sono mostrati nei data sheet [2],[3] e [4]. Si vede che per questi componenti la resistenza in continua dell'avvolgimento è circa di una cinquantina di milliohm a temperatura ambiente. Quando lavorano la temperatura sale di circa $\Delta T=40^\circ\text{C}$ e la resistenza aumenta di circa il $15\,%$ . Dal data sheet [4] si vede che a corrente molto piccola, l'induttanza di questo particolare induttore è molto al di sopra del valore nominale.

MOS

Avendo scelto una topologia con interruttore lo-side, serve un mos a canale N. Il processore di Arduino è alimentato a $5\,\text{V}$ , sembrerebbe che usando un MOS logic-level lo si possa pilotare direttamente. In realtà il processore non riesce ad erogare abbastanza corrente per accendere e spegnere il mos in modo sufficientemente veloce, per cui servirà un MOS driver alimentato a $12\,\text{V}$ .

La scelta del MOS consiste nello specificare due o tre parametri: massima tensione $V_{DS}\,$ quando il MOS è spento, la massima resistenza fra drain e source $r_{DSon}\,$ quando è acceso ed eventualmente il tipo di MOS, logic level oppure standard.

La tensione massima vista dal MOS è pari a $V_{i}\,$ , quindi serve un MOS con $V_{DSMAX}>60\,\text{V}$ , in modo da avere un minimo di margine. Probabilmente un MOS da 100V costituisce una scelta migliore.

La resistenza drain source quando è acceso dipende dalla caduta di tensione che si è disposti ad accettare quando il MOS conduce. Una scelta ragionevole è che la caduta di tensione massima sul mos possa arrivare all'1% della tensione di ingresso, quindi $V_{DSon}=0.5\text{V}\,$ . Essendo il MOS una resistenza, conoscendo la caduta di tensione ammessa e la corrente massima che lo attraversa, si determina che $r_{DSonHOT}=\frac{0.5\text{V}}{4.4\text{A}}=114\,\text{m}\Omega$ . Questa è la resistenza del mos a caldo, quando lavora, mentre sul data sheet si trova la resistenza a freddo, con il silicio a temperatura ambiente. Il rapporto fra le due resistenze è di circa 2, quando il mos è circa alla sua massima temperatura. In questo caso la temperatura non dovrebbe salire troppo, visto le piccole correnti in gioco e il fatto che il circuito sarà in un ambiento a temperatura non troppo calda, per cui si può assumere un rapporto di circa 1.5. Questo significa che sul catalogo bisogna cercare un MOS con una tensione di lavoro di 60V (o anche 100V) e $r_{DSon}=\frac{114\text{m}\Omega}{1.5}=\,76\text{m}\Omega$ Due delle centinaia di possibili candidati sono in [5] e [6]. Si osservi la specifica di corrente media non entra praticamente mai nella scelta del MOS, perché se questo viene scelto in base alla sua resistenza drain source in conduzione, la corrente sopportabile dal dispositivo è quasi sempre molto maggiore di quella effettivamente circolante.

Il MOS OnSemi logic level richiede per essere acceso richiede sul gate circa 10nC. Ammesso che il processore riesca a fornire 20mA per tutta la durata della commutazione, il tempo di commutazione è, come ordine di grandezza $t_{com}=\frac{10\text{nC}}{20\text{mA}}=500\,\text{ns}$ un po' lungo rispetto ai normali tempi di commutazione dei mos. Un tempo di commutazione lungo comporta dissipazione nel MOS ogni volta che commuta. Si noti che questa è solo una stima grossolana del tempo di commutazione, il calcolo esatto è abbastanza più complicato e spesso non si hanno dal data sheet i valori per il calcolo.