Elettrotecnica e non solo (admin)
Un gatto tra gli elettroni (IsidoroKZ)
Esperienza e simulazioni (g.schgor)
Moleskine di un idraulico (RenzoDF)
Il Blog di ElectroYou (webmaster)
Idee microcontrollate (TardoFreak)
PICcoli grandi PICMicro (Paolino)
Il blog elettrico di carloc (carloc)
DirtEYblooog (dirtydeeds)
Di tutto... un po' (jordan20)
AK47 (lillo)
Esperienze elettroniche (marco438)
Telecomunicazioni musicali (clavicordo)
Automazione ed Elettronica (gustavo)
Direttive per la sicurezza (ErnestoCappelletti)
EYnfo dall'Alaska (mir)
Apriamo il quadro! (attilio)
H7-25 (asdf)
Passione Elettrica (massimob)
Elettroni a spasso (guidob)
Bloguerra (guerra)
Indice |
Introduzione
In questo articolo espongo alcuni esercizi sulla semplificazione degli schemi a blocchi funzionali. Nell' altro mio articolo ( al seguente link: http://www.electroyou.it/mrc/wiki/operazioni-sugli-schemi-a-blocchi-funzionali ), relativo a questo argomento, ho esaminato le varie operazioni che si possono eseguire sugli schemi a blocchi.
Un ulteriore metodo è quello denominato delle uscite singole, si esamina lo schema e si ricava l' espressione dell' uscita considerando l' apporto dei singoli blocchi. I primi due esercizi saranno svolti utilizzando questo metodo.
Esercizio n° 1
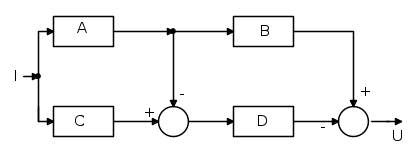
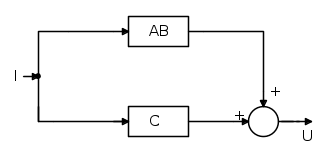
Dato il seguente schema a blocchi, ricavare la Funzione di Trasferimento ( FdT ):
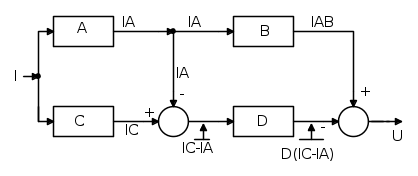
Dallo schema a blocchi, di cui sopra, possiamo ricavare le varie espressioni matematiche all' uscita di ogni blocco, nel seguente disegno riporto tali espressioni:
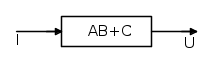
Da cui ottengo:
quindi sviluppando, risulta:
Esercizio n° 2
Dato il seguente schema a blocchi, ricavare la Funzione di Trasferimento ( FdT ):
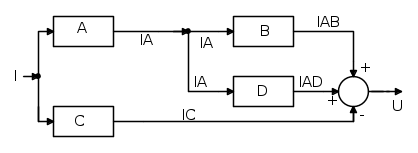
Dallo schema a blocchi, di cui sopra, possiamo ricavare le varie espressioni matematiche all' uscita di ogni blocco, nel seguente disegno riporto tali espressioni:
Da cui si ottiene:
U = IAD + IAB − IC
La FdT risulta:
Esercizio n° 3
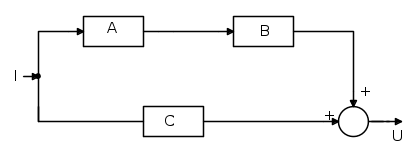
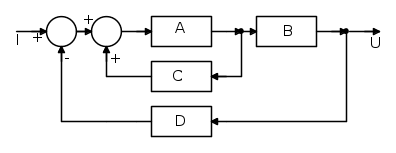
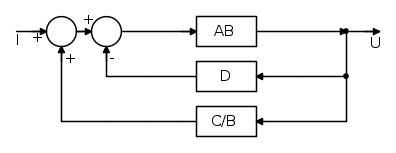
Dato il seguente schema a blocchi, ricavare la Funzione di Trasferimento ( FdT ):
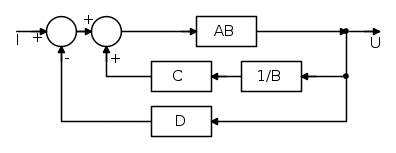
In questo caso, con un primo passaggio, si ottiene il seguente schema:
Da cui:
Quindi si ottiene la seguente:
ed infine:
Esercizio n° 4
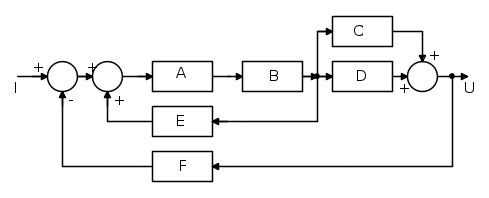
Dato il seguente schema a blocchi, ricavare la Funzione di Trasferimento:
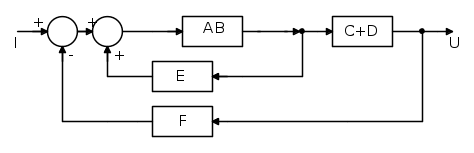
Lo schema a blocchi, di cui sopra, si può semplificare eseguendo i passaggi che vado ad esporre:
Dallo schema ricavo la seguente:
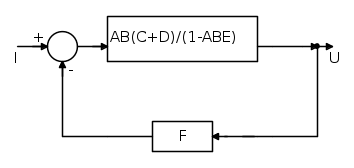
Dopo alcuni passaggi, che lascio al lettore, si ottiene:
Da cui:
Esercizio n° 5
Dato il seguente schema a blocchi, ricavare la Funzione di Trasferimento:
Lo schema a blocchi, di cui sopra, si può semplificare eseguendo i passaggi che vado ad esporre:
Dallo schema ricavo la seguente:
Dopo alcuni passaggi, che lascio al lettore, si ottiene:
Bibliografia
[1] Miei appunti scolastici.
