Indice |
Abstract
Questo articolo si propone di analizzare il comportamento di un classico sistema a retroazione in regime permanente, ossia a transitorio esaurito, sottoposto ad un opportuno segnale di ingresso. Al fine di rendere l'esposizione non troppo pesante, ho deciso di dividere l'articolo in due parti: nella prima saranno trattati gli effetti dei disturbi additivi sul sistema di controllo assieme a qualche esempio pratico; nella seconda, l'attenzione sarà rivolta alla classificazione dei sistemi di controllo in base agli errori di regolazione a regime (anche qui supportata da qualche esempio applicativo) e si farà un breve cenno per quel che riguarda la sensitività di un sistema. Le uniche conoscenze preliminari richieste sono la teoria della trasformata di Laplace e le regole basilari di trasformazione degli schemi a blocchi.
Regolazione automatica: schema di principio
In un qualsiasi sistema fisico, quando viene applicato un segnale all'ingresso di uno dei suoi elementi, si ingenera una "reazione" temporanea nota come risposta transitoria: le modalità con le quali si esplica questo fenomeno (durata temporale, ampiezza massima raggiunta in uscita, ecc.) sono dipendenti dalle caratteristiche intrinseche del sistema stesso. Una volta esaurito il transitorio, il sistema permane in una condizione di regime: si sono instaurate dunque delle condizioni statiche, anch'esse legate alle peculiarità del sistema e al tipo di sollecitazione applicata in ingresso e che permettono, soprattutto, di valutarne le prestazioni in termini di precisione, stabilità e robustezza.
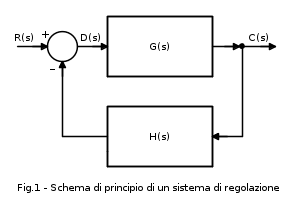
Lo schema di principio di un sistema di regolazione automatica è riportato in Fig.1:
in cui le varie grandezze hanno il seguente significato:
- R(s) è la t.d.L. (trasformata di Laplace) del segnale di ingresso o di riferimento (nel caso dei regolatori);
- C(s) è la t.d.L. della grandezza controllata o di uscita;
- D(s) è la t.d.L. del segnale differenza: D(s) = R(s) - C(s)H(s);
- G(s) è la funzione di trasferimento (f.d.t.) della linea di azione diretta;
- H(s) è la f.d.t. di retroazione (trasduttore del segnale di retroazione).
Per completezza, ricordiamo inoltre quanto segue:
- G(s)H(s) è la f.d.t. ad anello aperto o guadagno di anello;
-
 è la f.d.t. ad anello chiuso.
è la f.d.t. ad anello chiuso.
Un importante strumento per la stima di tali grandezze in condizioni statiche è il teorema del valore finale, il quale enuncia che se ![\mathcal{L}[f(t)]=F(s)](/mediawiki/images/math/d/a/2/da2f970e0ce2a8e3c27a1fcfb75f7364.png) allora:
allora:

ove il limite a primo membro esiste qualora la funzione F(s) non presenti poli a parte reale positiva, mentre l'esistenza del limite a secondo membro non implica necessariamente quella del primo.
Nel caso di sistemi di regolazione, il segnale di riferimento R è costante ed il suo valore dipende da quello che deve assumere la grandezza regolata e dal coefficiente di reazione H; supponendo infatti che G(s) ed H(s) non abbiamo poli nulli, in condizioni di regime le f.d.t. delle linee di andata e retroazione si riducono a delle costanti K ed H (avendo applicato il teorema del valore finale). Lo schema di Fig.1 può essere quindi così ridisegnato:
La grandezza controllata assume quindi l'espressione seguente:
![C=R\frac{K}{1+KH}\,\,\,\,\,\,\,\,\,\,\,\,\,[1]](/mediawiki/images/math/d/9/4/d94c6783d1bc5ab4885dae30838a2135.png)
e, nel caso in cui KH >> 1:
![C_{0}=\frac{R}{H}\,\,\,\,\,\,\,\,\,\,\,\,\,[2]](/mediawiki/images/math/4/5/b/45bfbc53bae676d5a86f628f084c785a.png)
Il termine KH prende adesso il nome di guadagno statico di anello (è da notare che la condizione  dovrebbe essere raggiunta con
dovrebbe essere raggiunta con  ed H costante, altrimenti C tenderebbe a 0, oppure per avere un certo valore di C il segnale di riferimento R dovrebbe assumere un valore infinitamente grande).
ed H costante, altrimenti C tenderebbe a 0, oppure per avere un certo valore di C il segnale di riferimento R dovrebbe assumere un valore infinitamente grande).
E' chiaro però che, nelle applicazioni reali, il valore di K non è infinitamente grande a parità di valore di R, per cui la grandezza controllata C assume un valore un po' inferiore (dato dalla [1]): si dice in tal caso che la grandezza regolata è affetta da un certo errore E. Analiticamente esso rappresenta lo scostamento di C dal valore ideale dato dalla [2]:
![E=C_{0}-C\,\,\,\,\,\,\,\,\,\,\,\,\,[3]](/mediawiki/images/math/a/7/1/a7182500a105639ccd129dd38d641071.png)
Sostituendo la [1] e la [2] nella [3], otteniamo:
![E=\frac{R}{H}-R\frac{K}{1+KH}=\frac{R}{H}\frac{1}{1+KH}=\frac{C_{0}}{1+KH}\,\,\,\,\,\,\,\,\,\,\,\,\,[4]](/mediawiki/images/math/5/a/d/5ad602d0db6788cabd3101af55d3b777.png)
da cui si vede che l'errore di regolazione a regime è tanto minore quanto più è elevato il guadagno statico di anello KH. Il segnale differenza dato da:
![D=R-HC\,\,\,\,\,\,\,\,\,\,\,\,\,[5]](/mediawiki/images/math/d/3/4/d34aa9c64347e39c64590a6c518fbc36.png)
in base alla [1] diventa:
![D=R-HR\frac{K}{1+KH}=\frac{R}{1+KH}\,\,\,\,\,\,\,\,\,\,\,\,\,[6]](/mediawiki/images/math/4/0/0/4006bb9a3b5978259659e89f60a1f338.png)
Tale segnale fornisce una indicazione sulla precisione della regolazione e molte volte, impropriamente, viene indicato come segnale errore. Confrontando la [4] e la [6] ci rendiamo conto invece che essi coincidono solo nel caso in cui H sia unitario.
1. Effetto dei disturbi in un sistema di regolazione
L'errore di regolazione, per come lo abbiamo definito, riveste nella pratica un'importanza relativamente modesta; se infatti applichiamo in ingresso un segnale del tipo:
![R^{'}=\frac{R}{H}\frac{1+KH}{K}\,\,\,\,\,\,\,\,\,\,\,\,\,[7]](/mediawiki/images/math/3/f/6/3f66163ac65edabf6feb1740b00bb89e.png)
la grandezza controllata assume il valore:
![C=R^{'}\frac{K}{1+KH}=\frac{R}{H}=C_{0}\,\,\,\,\,\,\,\,\,\,\,\,\,[8]](/mediawiki/images/math/4/f/e/4fecdebe61eddce099a0ebc2189fda93.png)
avendo di fatto compensato l'errore. Nei sistemi reali agiscono però altri segnali indesiderati o variazioni dei parametri intrinseci (dovuti all'inevitabile degrado nel tempo dei componenti, ma non solo) che causano comunque uno scostamento della grandezza controllata dal suo valore ideale; nella fattispecie, distinguiamo:
- disturbi additivi: nel caso si tratti di segnali esterni non desiderati che entrano in qualche elemento del sistema;
- disturbi parametrici: nel caso si tratti di variazioni non desiderate di un parametro di qualche elemento del sistema (ad esempio il fattore di amplificazione di un transistor per effetto di variazioni termiche).
La seconda categoria di disturbi, in prima istanza, è riconducibile alla prima perché spesso la variazione di un parametro avviene per una causa esterna al sistema; ad esempio, la variazione di amplificazione per effetto di variazioni termiche può essere ricondotta all'effetto di un segnale di temperatura entrante nell'amplificatore. Nella nostra trattazione pertanto consideriamo soltanto disturbi additivi; questi segnali possono entrare in qualsiasi punto dell'anello di regolazione: all'ingresso assieme al segnale di riferimento, in un punto generico della linea di azione diretta, all'uscita, oppure in un punto della linea di retroazione.
1.1 Disturbo agente in uscita
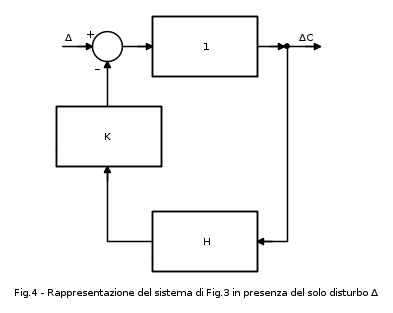
La situazione di Fig.3 è in pratica piuttosto frequente (un esempio può essere fornito dalla caduta di tensione ai morsetti di un motore elettrico, per effetto della variazione di carico, in un sistema di regolazione di tensione); esso viene supposto costante (il che è lecito visto che siamo in condizioni statiche). Data per scontata l'ipotesi di linearità del nostro sistema, è possibile applicare il principio di sovrapposizione degli effetti: consideriamo pertanto soltanto l'effetto del disturbo in uscita e semplifichiamo lo schema di Fig.3 come segue:
dove è stato inserito un blocco con f.d.t. unitaria equivalente ad un collegamento diretto. Il valore di C per effetto del disturbo vale:
![\Delta C=\Delta \frac{1}{1+KH}\,\,\,\,\,\,\,\,\,\,\,\,\,[9]](/mediawiki/images/math/d/e/b/deb999d43cd9aad4406ee8ee7ceac3ff.png)
Come vediamo, il disturbo Δ ha un'influenza sulla grandezza controllata tanto minore quanto più elevato è il guadagno statico di anello (al limite, il suo effetto è nullo per KH che diverge all'infinito).
Da un punto di vista fisico, l'effetto della regolazione sulla riduzione del disturbo può essere spiegata considerando che la variazione ΔC per effetto del disturbo provoca una variazione del segnale di retroazione di una entità pari a:
![H\Delta C=H\frac{\Delta }{1+KH}\,\,\,\,\,\,\,\,\,\,\,\,\,[10]](/mediawiki/images/math/e/f/2/ef27547900236897939377da801bfc0d.png)
A sua volta, la variazione del segnale di retroazione provoca una variazione di segno opposto del segnale differenza:
![\Delta D=-H\frac{\Delta }{1+KH}\,\,\,\,\,\,\,\,\,\,\,\,\,[11]](/mediawiki/images/math/b/a/6/ba62a8e18f05dfd2a6e7c76d32aecde7.png)
che, amplificata del fattore K, provoca una variazione del segnale C' di Fig.3:
![\Delta C^{'}=-KH\frac{\Delta }{1+KH}\,\,\,\,\,\,\,\,\,\,\,\,\,[12]](/mediawiki/images/math/0/b/0/0b01d03aa5fa60361e0683b2a47546c3.png)
Per finire, sommando il disturbo, avremo una variazione complessiva della grandezza controllata pari a:
![\Delta C=\Delta C^{'}+\Delta =-KH\frac{\Delta }{1+KH}+\Delta =\frac{\Delta }{1+KH}\,\,\,\,\,\,\,\,\,\,\,\,\,[13]](/mediawiki/images/math/f/c/e/fceba0e06001064e81c48b62c55a0ccf.png)
1.2 Disturbo agente in ingresso
L'effetto di riduzione del disturbo è tanto più efficace quanto più esso entra in prossimità dell'uscita del sistema; supponiamo adesso che il disturbo agisca all'ingresso della linea di azione diretta:
Esso equivarrebbe ad un disturbo sull'uscita di valore KΔ, per cui la variazione della grandezza controllata risulterebbe pari a:
![\Delta C=K\frac{\Delta }{1+KH}\,\,\,\,\,\,\,\,\,\,\,\,\,[14]](/mediawiki/images/math/f/1/f/f1f1be362d1f65a6601d7ade9220293f.png)
e per K divergente tenderebbe al valore finito  anziché al valore nullo.
anziché al valore nullo.
Nel dimensionamento di un sistema di regolazione, occorre quindi che i primi elementi della catena (complesso di regolazione) siano il più possibile esenti da disturbi, in quanto il sistema di regolazione è in grado di correggere in prevalenza quelli che i originano verso l'uscita del sistema (complesso regolato). Analoghe considerazioni valgono per i disturbi che si originano nei trasduttori della linea di retroazione, dal momento che essi si presentano, tramite il nodo sommatore, all'ingresso della linea di azione diretta.
2. Esempi applicativi
Qualche esempio applicativo chiarirà ulteriormente quanto sopra esposto.
Esempio 1
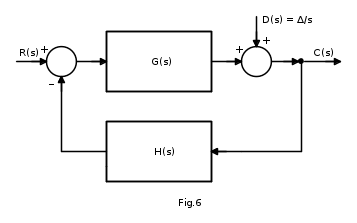
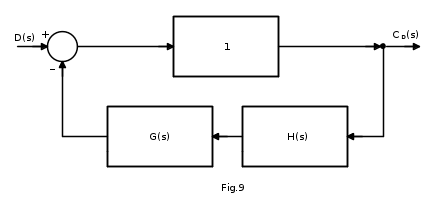
Si determini l'influenza del disturbo D(s) sulla risposta, in condizioni di regime permanente del sistema di Fig.6, assimilando D(s) ad un gradino di ampiezza Δ che agisce in uscita sulla linea di azione diretta:
Per valutare l'effetto del disturbo sulla risposta del sistema, applichiamo il principio di sovrapposizione degli effetti: consideriamo l'uscita come somma dell'uscita CR(s), dovuta al segnale R(s), e CD(s), dovuta al disturbo. Per D(s)=0 si ha:
con:
![C_{R}(s)=R(s)\frac{G(s)}{1+G(s)H(s)}\,\,\,\,\,\,\,\,\,\,\,\,\,[15]](/mediawiki/images/math/a/a/6/aa6cc4535cf3fdd385ad38dbf9f3aaed.png)
Per R(s)=0, applicando le regole degli schemi a blocchi:
ed ulteriormente semplificabile come segue:
In questo caso l'uscita vale:
![C_{D}(s)=D(s)\frac{1}{1+G(s)H(s)}\,\,\,\,\,\,\,\,\,\,\,\,\,[16]](/mediawiki/images/math/4/9/d/49db49a19bbe646dee513fc9adbb03ae.png)
Si ha quindi:
![C_{RD}(s)=C_{R}(s)+C_{D}(s)=R(s)\frac{G(s)}{1+G(s)H(s)}+D(s)\frac{1}{1+G(s)H(s)}\,\,\,\,\,\,\,\,\,\,\,\,\,[17]](/mediawiki/images/math/5/7/c/57ccbf77fadd8752d622ad1b3887d777.png)
L'effetto che vogliamo valutare, ovvero la variazione dell'uscita in presenza del segnale di disturbo, è dato dalla differenza tra l'uscita affetta da disturbo CRD(s) e quella da esso immune CR(s), per cui la variazione ΔC(s) rilevata in uscita è:

![-R(s)\frac{G(s)}{1+G(s)H(s)}\,\,\,\,\,\,\,\,\,\,\,\,\,[18]](/mediawiki/images/math/8/6/3/8637f1ab534b7a267c1bc713361e524c.png)
ovvero:
![\Delta C(s)=D(s)\frac{1}{1+G(s)H(s)}\,\,\,\,\,\,\,\,\,\,\,\,\,[19]](/mediawiki/images/math/f/5/5/f550316d49a282f1e825c8f08237dea7.png)
pertanto, la variazione di uscita è dovuta al solo disturbo (come è giusto che sia essendo il sistema lineare).
Per determinare l'effetto in condizioni di regime permanente, applichiamo il teorema del valore finale; indicando con  la variazione dell'uscita dovuta al disturbo in condizioni statiche, si ha:
la variazione dell'uscita dovuta al disturbo in condizioni statiche, si ha:
![\Delta C_{\Delta }(\infty)=\lim_{s \to 0 }s\frac{\Delta }{s}\frac{1}{1+G(s)H(s)}=\frac{\Delta }{1+G(s)H(s)}\,\,\,\,\,\,\,\,\,\,\,\,\,[20]](/mediawiki/images/math/4/b/f/4bf1b8a0677cfc52d7ddc94b4162be6a.png)
Per quanto supposto in precedenza (ossia assenza di poli nell'origine per la funzione di anello aperto), la [20] si riduce al termine  , che rappresenta proprio l'influenza del disturbo Δ sulla risposta statica. In altri termini, il disturbo risulta attenuato di una quantità
, che rappresenta proprio l'influenza del disturbo Δ sulla risposta statica. In altri termini, il disturbo risulta attenuato di una quantità  e, passando al limite, se KH tende ad infinito (H costante e K tendente all' infinito) il disturbo non avrebbe alcun effetto sull'uscita, diventando nullo il termine
e, passando al limite, se KH tende ad infinito (H costante e K tendente all' infinito) il disturbo non avrebbe alcun effetto sull'uscita, diventando nullo il termine  .
.
Esempio 2
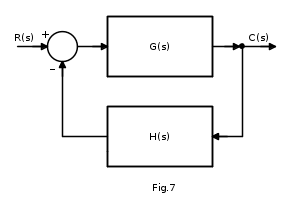
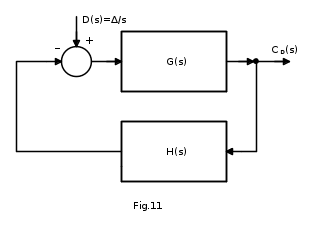
Si determini l'azione del disturbo D(s) che agisce all'ingresso della linea di azione diretta, sulla risposta del sistema di Fig.10:
Analogamente a quanto fatto nel primo esempio, applichiamo il principio di sovrapposizione degli effetti: per R(s)=0 si ha:
che ridisegnamo come segue:
quindi:
![C_{D}(s)=D(s)\frac{G(s)}{1+G(s)H(s)}\,\,\,\,\,\,\,\,\,\,\,\,\,[21]](/mediawiki/images/math/3/c/7/3c7e4a7b7dbca4913c3b1e741feb6163.png)
ed in condizioni di regime permanente:
![\Delta C_{\Delta }(\infty)=\lim_{s \to 0 }s\frac{\Delta }{s}\frac{G(s)}{1+G(s)H(s)}=\frac{\Delta G(s)}{1+G(s)H(s)}\,\,\,\,\,\,\,\,\,\,\,\,\,[22]](/mediawiki/images/math/2/4/1/241b6b69089dcd0050938674e517a0e6.png)
Per le solite ipotesi in cui G(s)=K e H(s)=H si ha:
![\Delta C_{\Delta }(\infty)=\frac{\Delta K}{1+KH}\,\,\,\,\,\,\,\,\,\,\,\,\,[23]](/mediawiki/images/math/6/0/a/60ad88389aa16fe7e007101f8ca6a61b.png)
ed in tal caso il disturbo non sarebbe annullato neanche se  avendosi
avendosi  .
.
E' evidente quindi, come sia di notevole importanza avere i primi stadi del sistema di regolazione privi di disturbi. Fisicamente si nota che sia R(s) che D(s) incontrano lo stesso blocco G(s) prima dell'uscita e quindi vengono entrambi amplificati; per ridurre l'effetto del disturbo non rimane allora che aumentare il livello del segnale R(s) a valori molto maggiori di quelli del disturbo (cosa peraltro non sempre fattibile nelle applicazioni reali).
Esempio 3
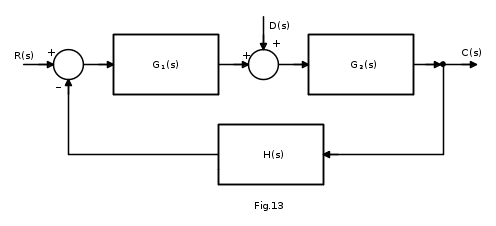
Si studi il caso in cui il disturbo a gradino di ampiezza Δ entri in un punto intermedio della linea di azione diretta:
Procedendo come nei casi precedenti, per R(s)=0 ed applicando opportunamente le regole di semplificazione dei blocchi, si perviene al seguente schema:
L'uscita per il sistema di Fig.14 risulta pertanto:
![C_{D}(s)=D(s)\frac{G_{2}(s)}{1+G_{1}(s)G_{2}(s)H(s)}\,\,\,\,\,\,\,\,\,\,\,\,\,[24]](/mediawiki/images/math/3/e/b/3eb3af2586003cd460db7fd30fb66d39.png)
In condizioni statiche, avendosi  ,
,  e H(s)=H, otteniamo:
e H(s)=H, otteniamo:
![\Delta C_{\Delta }(\infty)=\lim_{s \to 0 }s\frac{\Delta }{s}\frac{G_2(s)}{1+G_1(s)G_2(s)H(s)}=\frac{\Delta K_2}{1+K_1K_2H}\,\,\,\,\,\,\,\,\,\,\,\,\,[25]](/mediawiki/images/math/4/1/b/41ba26da3884147829e32602992ecaa1.png)
che mostra come l'effetto del disturbo risulti attenuato se si eleva K1 e si riduce K2. Quindi, in generale, per avere un sistema con un buon comportamento nei riguardi dei disturbi, occorre che i primi stadi della catena abbiano un guadagno elevato ma, per quanto visto nel secondo esempio, questi stadi devono essere privi di disturbi.
Esempio 4
Si valuti l'effetto di un disturbo  agente sulla linea di retroazione in ingresso al blocco trasduttore H(s) nello schema di Fig.15:
agente sulla linea di retroazione in ingresso al blocco trasduttore H(s) nello schema di Fig.15:
Sulla stessa linea risolutiva dei precedenti esempi, per R(s)=0 lo schema di Fig.15 è equivalente al seguente:
L'uscita vale quindi:
![C_{D}(s)=\frac{-G(s)H(s)D(s)}{1-[-G(s)H(s)]}=\frac{-G(s)H(s)D(s)}{1+G(s)H(s)}\,\,\,\,\,\,\,\,\,\,\,\,\,[26]](/mediawiki/images/math/7/f/8/7f83bbee74d413f7a972bb151c9514df.png)
Applicando il teorema del valore finale e supponendo f.d.t. esenti da poli semplici nell'origine, perveniamo alla relazione seguente:
![\Delta C_{\Delta }(\infty)=\lim_{s \to 0 }s\frac{\Delta }{s}\frac{-G(s)H(s)}{1+G(s)H(s)}=-\frac{\Delta KH}{1+KH}\,\,\,\,\,\,\,\,\,\,\,\,\,[27]](/mediawiki/images/math/c/1/b/c1ba633f0ab910aad8b0aa59b236c238.png)
da cui deduciamo che, nei casi pratici in cui KH >> 1, risulta  , vale a dire che il disturbo resta pressoché invariato. E' allora estremamente importante avere la linea di reazione totalmente esente da disturbi, perché essi non vengono sensibilmente attenuati.
, vale a dire che il disturbo resta pressoché invariato. E' allora estremamente importante avere la linea di reazione totalmente esente da disturbi, perché essi non vengono sensibilmente attenuati.
Esempio 5
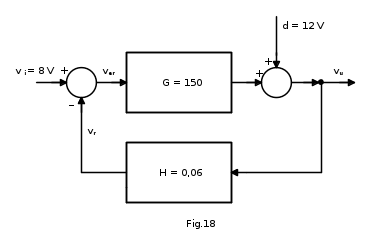
Vediamo infine un esempio numerico; dato il sistema rappresentato in Fig.17:
si determini:
- a) la tensione di uscita vu, la tensione della linea di retroazione vr, l'errore ver;
- b) l'effetto della retroazione negativa, quando è presente in uscita un disturbo d = 12 V;
- c) si confrontino i risultati ottenuti al punto b) con i risultati che si hanno in assenza della linea di retroazione.
a) Per calcolare i valori di vu, vr e ver, occorre determinare la f.d.t. ad anello chiuso:

Le grandezze richieste valgono pertanto:



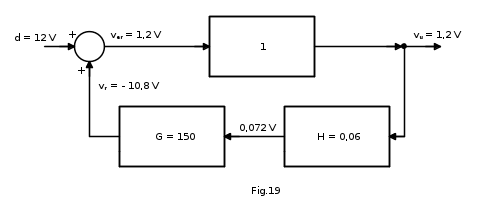
b) Per valutare l'effetto del disturbo in uscita consideriamo il seguente schema:
Annullando l'ingresso, si ha:

La tensione di uscita vud è:

da cui derivano tutte le altre grandezze della catena:



Schematicamente:
Per valutare l'effetto benefico della retroazione, si compongono le situazioni illustrate in Fig.16 e Fig.18, ottenendo così la tensione di uscita totale vuT data da:

Si ha inoltre:

e l'errore vale:

In uscita dal blocco G la tensione vale:

che sommata al disturbo fornisce un segnale pari a:

Schematicamente:
c) Se il sistema di Fig.17 fosse a catena aperta, il segnale di disturbo si sarebbe propagato interamente in uscita:

con variazione della grandezza pari a 12 V.
In presenza della retroazione invece, lo stesso disturbo d = 12 V viene ridotto e l'uscita, essendo  varia di 1,2 V anziché di 12 V.
varia di 1,2 V anziché di 12 V.
Bibliografia
[1] Appunti e dispense del corso di Controlli Automatici tenuto presso la facoltà di Ingegneria Elettronica dell'Università degli Studi di Palermo; [2] Giuseppe Sabatini - Esercizi e applicazioni di Elettronica Industriale con note teoriche, Edizioni Cupido

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)