Elettrotecnica e non solo (admin)
Un gatto tra gli elettroni (IsidoroKZ)
Esperienza e simulazioni (g.schgor)
Moleskine di un idraulico (RenzoDF)
Il Blog di ElectroYou (webmaster)
Idee microcontrollate (TardoFreak)
PICcoli grandi PICMicro (Paolino)
Il blog elettrico di carloc (carloc)
DirtEYblooog (dirtydeeds)
Di tutto... un po' (jordan20)
AK47 (lillo)
Esperienze elettroniche (marco438)
Telecomunicazioni musicali (clavicordo)
Automazione ed Elettronica (gustavo)
Direttive per la sicurezza (ErnestoCappelletti)
EYnfo dall'Alaska (mir)
Apriamo il quadro! (attilio)
H7-25 (asdf)
Passione Elettrica (massimob)
Elettroni a spasso (guidob)
Bloguerra (guerra)
Indice |
Premessa
Ho notato che sovente nel forum ci sono richieste che, dati degli schemi, si debba trovare la resistenza equivalente e molte di queste volte non si riesca a farlo.
Ho pensato allora di riportare qui degli esercizi svolti un po' da me o che ho trovato in giro su alcuni libri, su qualche sito, o sul forum stesso.
Per aiutare le persone che vogliono imparare metterò prima tutta una carrellata di esercizi, così se uno vuole li può svolgere tranquillamente, e poi, in fondo, elencherò le varie soluzioni per una eventuale verifica.
Sperando di aver fatto cosa gradita e di non aver commesso troppi errori nello svolgere gli esercizi vi lascio l'elenco.
P.S. per ogni esercizio sarà da calcolare la resistenza equivalente, per cui non lo starò a scrivere ogni volta.
Esercizi
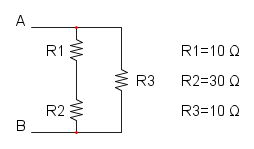
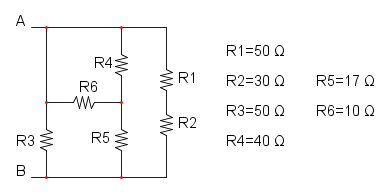
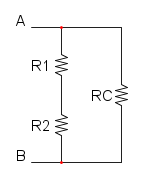
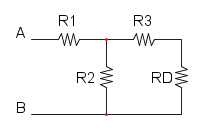
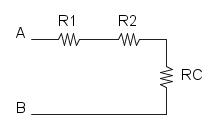
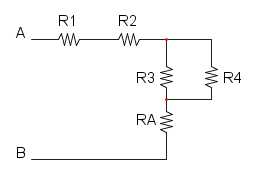
Es. 1
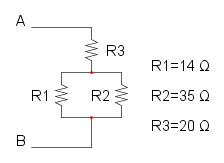
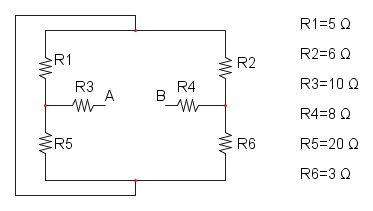
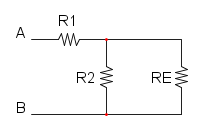
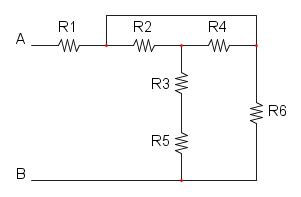
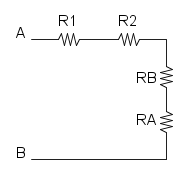
Es. 2
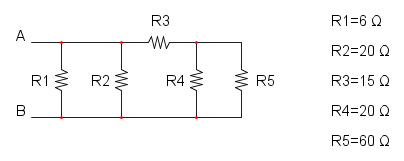
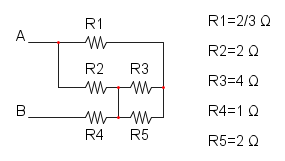
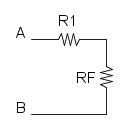
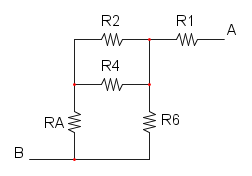
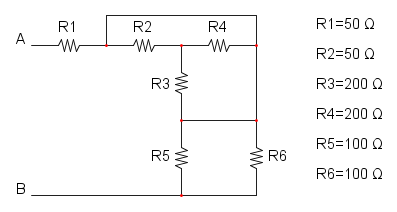
Es. 3
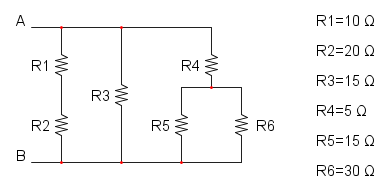
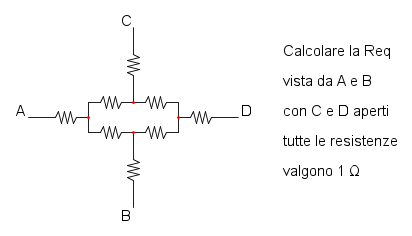
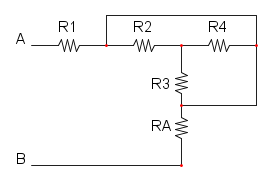
Es. 4
Es. 5
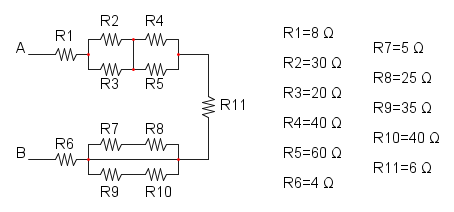
Es. 6
Es. 7
Es. 8
Es. 9
Es. 10
Es. 11
Es. 12
Es. 13
Es.14
Es. 15
Es. 16
Es. 17
Es. 18
Es. 19
Es. 20
Es. 21
Es. 22
Es. 23
Soluzioni
Per agevolare la lettura e l'utente che vuole imparare farò tutti i passaggi e allegherò ogni volta il disegno equivalente che si ha dopo una semplificazione.
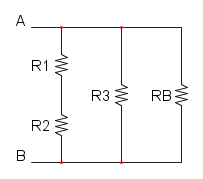
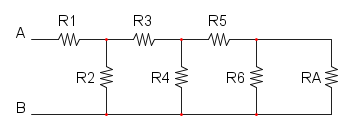
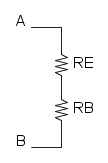
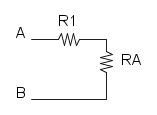
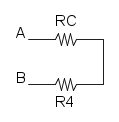
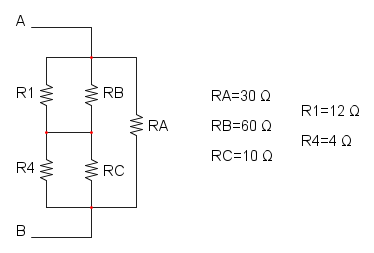
Es. 1
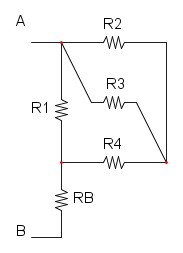
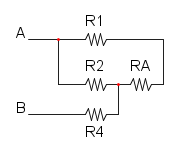
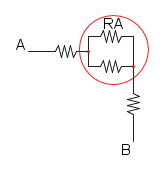
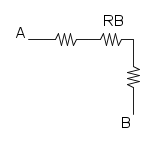
Come prima cosa si può notare che si ha R1 in serie con R2, per cui si trova:
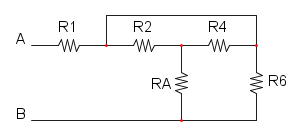
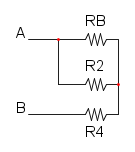
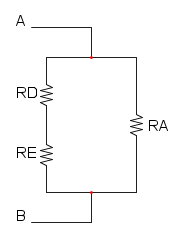
e si riduce a questo:
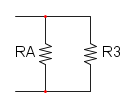
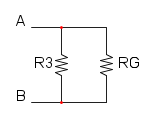
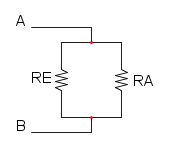
e per finere abbiamo RA in parallelo con R3:
![R_{eq} = R_A//R_3=\frac{R_A \cdot R_3}{R_A + R_3}=\frac {40\cdot10}{40+10}={\color[RGB]{0,105,50} 8\ \Omega}](/mediawiki/images/math/0/a/b/0abdaa292883ef630aa09ae1e59b699e.png)
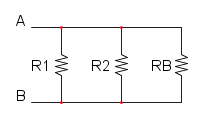
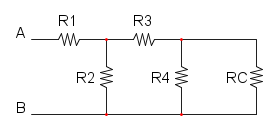
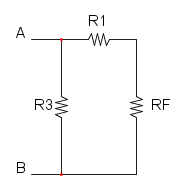
Es. 2
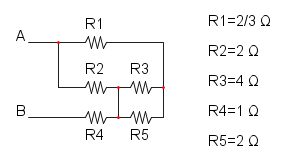
Abbiamo che R1 è in parallelo con R2 e si ha:
e si riduce così:
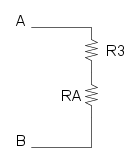
Ora abbiamo che R3 è in serie con RA e otteniamo:
![R_{eq}=R_3+R_A=20+10={\color[RGB]{0,105,50} 30\ \Omega}](/mediawiki/images/math/7/8/e/78e55edfdb2be9fa1e08b96599e067da.png)
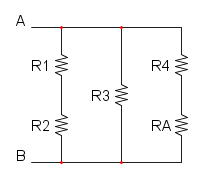
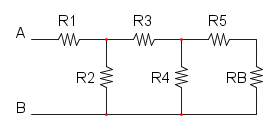
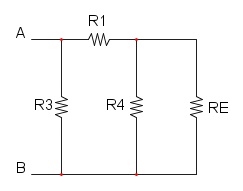
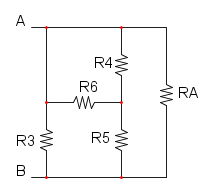
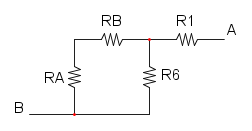
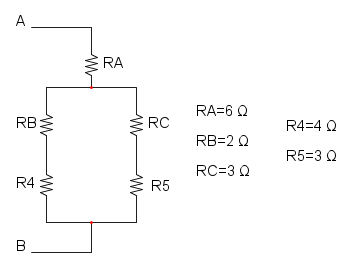
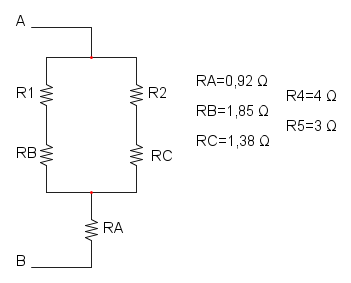
Es. 3
Qui abbiamo che R4 è in parallelo a R5 e otteniamo:
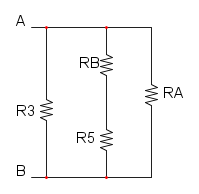
e ridisegnamo:
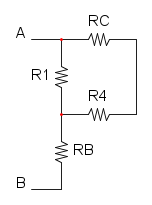
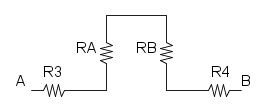
ora abbiamo che RA è in serie con R3 e otteniamo:
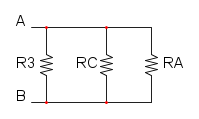
e diventa:
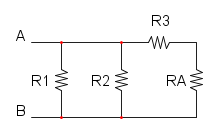
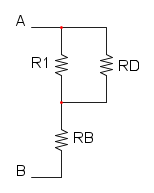
e per finire abbiamo R1, R2 e RB che sono in parallelo:
![R_{eq}=R_1//R_2//R_B=\frac{1}{\frac{1}{6}+\frac{1}{20}+\frac{1}{30}}={\color[RGB]{0,105,50} 4\ \Omega}](/mediawiki/images/math/7/d/9/7d9b97aa2c8213c02c0cbb089a3b8142.png)
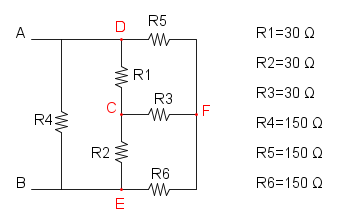
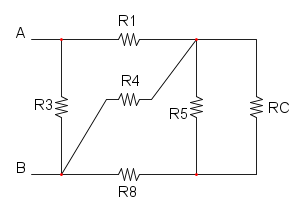
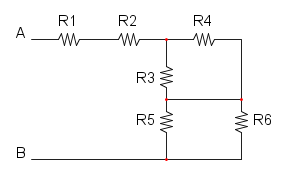
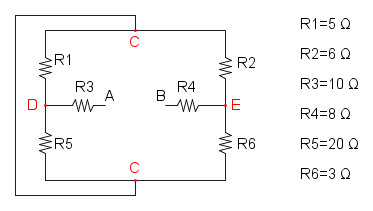
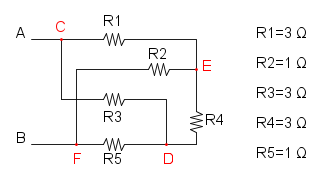
Es. 4
Partiamo col ridurre R5 e R6 che si trovano in parallelo e otteniamo:
e diventa:
ora abbiamo RA in serie con R4 e si ha:
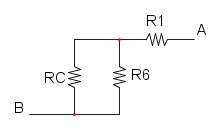
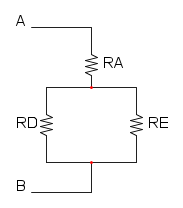
riduciamo ora R3 e RB che sono in parallelo:
e diventa:
ora possiamo semplificare R1 e R2 che sono in serie:
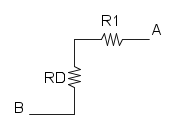
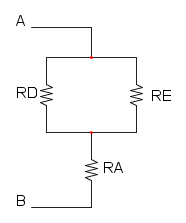
e ridisegnamo:
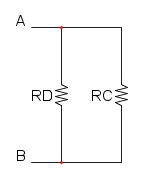
e per concludere abbiamo RD in parallelo a RC:
![R_{eq}=R_D//R_C=\frac{30\cdot 7,5}{30+7,5}={\color[RGB]{0,105,50} 6\ \Omega}](/mediawiki/images/math/f/c/8/fc884a40d3ce9c453487bb69a4dd9eeb.png)
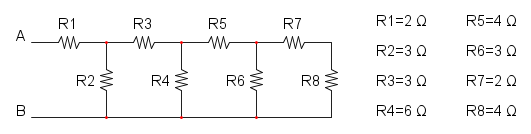
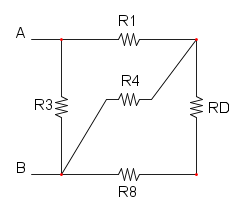
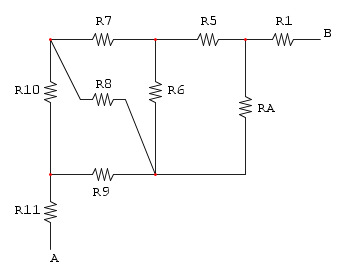
Es. 5
Partiamo col semplificare R7 e R8 che sono in serie:
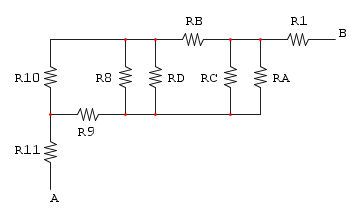
il disegno è:
ora semplifichiamo RA che è in parallelo con R6:
e ridisegnamo:
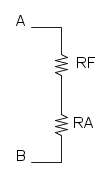
ora abbiamo RB in serie con R5:
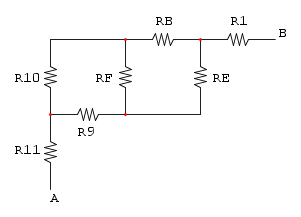
adesso abbiamo RC in parallelo con R4:
semplifichiamo RD con R3 che sono in serie:
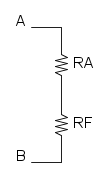
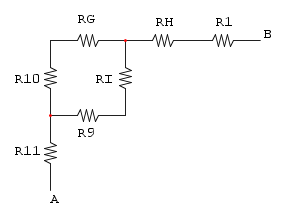
adesso abbiamo RE in parallelo a R2:
e per finire abbiamo RF in serie a R1:
![R_{eq}=R_F+R_1=2+2={\color[RGB]{0,105,50} 4\ \Omega}](/mediawiki/images/math/0/1/e/01e08e1b0717b654e7ce7740d0fd5847.png)
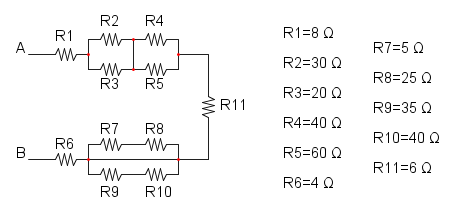
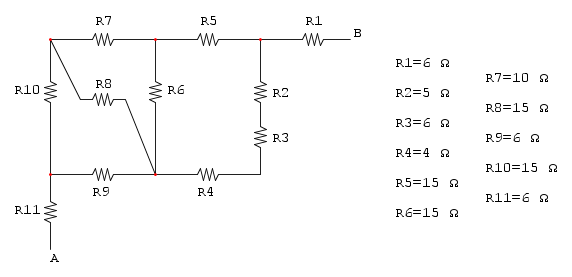
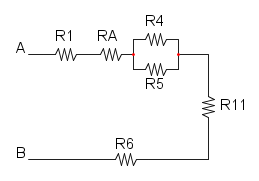
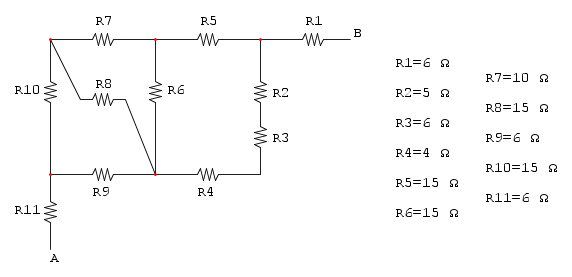
Es.6
Dallo schema si può intuire che le resistenze R7, R8, R9 e R10 non influiscono sul calcolo della Req in quanto sono collegate ad un cortocircuito e di conseguenza si possono eliminare:
possiamo cominciare ora col semplificare R2 in parallelo a R3:
continuiamo con R4 in parallelo con R5:
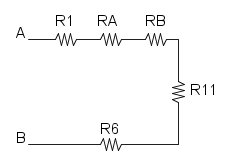
e per finire abbiamo la serie tra R1, RA, RB, R11 e R6:
![R_{eq}=R_1+R_A+R_B+R_{11}+R_6=8+12+24+6+4={\color[RGB]{0,105,50} 54\ \Omega}](/mediawiki/images/math/a/e/a/aea10fd686e533cd810c9366fe7c04e9.png)
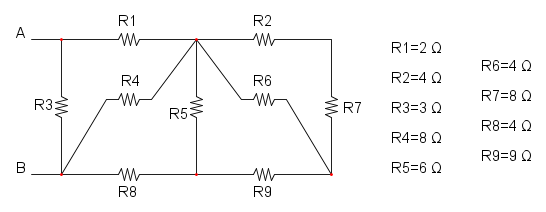
Es.7
Iniziamo con la serie tra R2 e R7:
proseguiamo col parallelo tra RA e R6:
continuiamo con la serie tra RB e R9:
ora riduciamo il parallelo tra RC e R5:
adesso semplifichiamo RD in serie con R8:
semplifichiamo RE in parallelo con R4:
ora abbiamo la serie tra RF e R1:
e per finire il parallelo tra RG e R3:
![R_{eq}=R_G//R_3=\frac{6\cdot 3}{6+3}={\color[RGB]{0,105,50} 2\ \Omega}](/mediawiki/images/math/d/6/9/d69e3e27b66088a46656ace3c453b46d.png)
Es.8
Cominciamo col semplificare R6 in serie a R7:
procediamo con il parallelo tra RA e R5:
semplifichiamo ora il parallelo tra R2 e R3:
continuiamo con la serie tra RC e R4:
ora R1 e RD si rovano in parallelo:
e per concludere abbiamo la serie tra RB e RE:
![R_{eq}=R_B+R_E=12+20={\color[RGB]{0,105,50} 32\ \Omega}](/mediawiki/images/math/7/2/a/72a0817a22ac2efd2ec4fd49c848ebc4.png)
Es.9
Incominciamo col semplificare la serie tra R1 e R2:
R4 e R6 si trovano in parallelo:
ora RB e R5 si trovano in serie:
e per concludere abbiamo il parallelo tra R3, RC e RA:
![R_{eq}=R_3//R_C//R_A=\frac{1}{\frac{1}{50}+\frac{1}{25}+\frac{1}{80}}={\color[RGB]{0,105,50} 13,8\ \Omega}](/mediawiki/images/math/b/f/7/bf788ca5838f87fe87cc79a6c1961dcd.png)
Es.10
Qui possiamo partire dalla serie tra R4 e R6:
proseguiamo con la serie tra R3 e R5:
ora il parallelo tra RA e RB:
e per concludere la serie tra R1, R2 e RC:
![R_{eq}=R_1+R_2+R_C=50+50+150={\color[RGB]{0,105,50} 250\ \Omega}](/mediawiki/images/math/4/7/0/4708c33d1cf1723227c6cd0357198e0d.png)
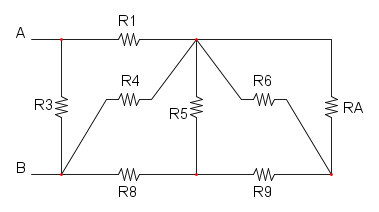
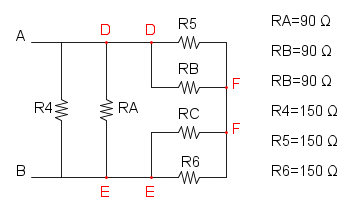
Per prima cosa qui si nota subito la serie tra R3 e R5:
a questo punto potrebbe sembrare che non vi sia più nulla da semplificare, oppure si potrebbe anche pensare che RA, R4 e R6 formino un triangolo, ma proviamo a disegnare lo schema in un'altra maniera:
così facendo ci si accorge che R2 e R4 sono in parallelo:
ora abbiamo la serie tra RA e RB:
poi abbiamo il parallelo tra RC e R6:
e per concludere la serie tra RD e R1:
![R_{eq}=R_D+R_1=77,3+50={\color[RGB]{0,105,50} 127,3\ \Omega}](/mediawiki/images/math/0/2/b/02bb502a21565c910fecdecda6516468.png)
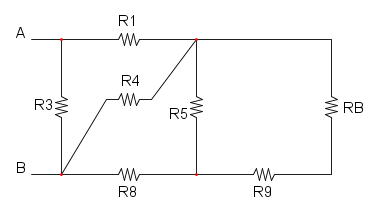
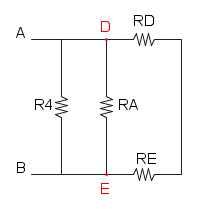
riduciamo R5 e R6 che si trovano in parallelo:
ora abbiamo il parallelo tra R3 e R4:
e per ultimo la serie tra R1, R2, RB e RA:
![R_{eq}=R_1+R_2+R_B+R_A=50+50+100+50={\color[RGB]{0,105,50} 250\ \Omega}](/mediawiki/images/math/3/2/d/32d3b586770158c0b34197fbf90e426d.png)
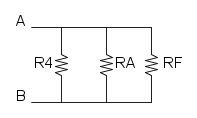
partiamo da R5 e R6 che sono sempre in parallelo:
a questo punto si può notare che le resistenze R2, R3 e R4 sono bypassate da un cortocircuito e quindi si possono eliminare:
a questo punto si ha solo la serie tra R1 e RA:
![R_{eq}=R_1+R_A=50+50={\color[RGB]{0,105,50} 100\ \Omega}](/mediawiki/images/math/6/2/a/62a350a7bb48b97f01a984cfcba76984.png)
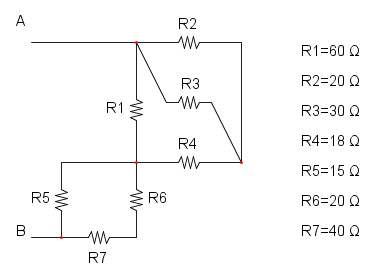
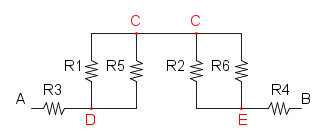
Es.11
Guardando lo schema ad occhio inesperto risulta difficile trovare una semplificazione; per cui possiamo ridisegnare lo schema e facilitarci le cose:
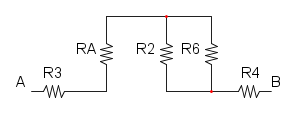
ora è tutto più chiaro e possiamo incominciare col semplificare R1 in parallelo con R5:
continuiamo col parallelo tra R2 e R6:
e per finire abbiamo la serie tra R3, RA, RB e R4:
![R_{eq}=R_3+R_A+R_B+R_4=10+4+2+8={\color[RGB]{0,105,50} 24\ \Omega}](/mediawiki/images/math/d/9/a/d9a0827ae553376d641e75cc5f610647.png)
Es.12
partiamo dal parallelo tra R3 e R5:
riduciamo ora la serie tra R1 e RA:
ora il parallelo tra RB e R2:
e per finire la serie tra RC e R4:
![R_{eq}=R_C+R_4=1+1={\color[RGB]{0,105,50} 2\ \Omega}](/mediawiki/images/math/1/a/8/1a85b82c6b8f9554fdf36d99d9d43f32.png)
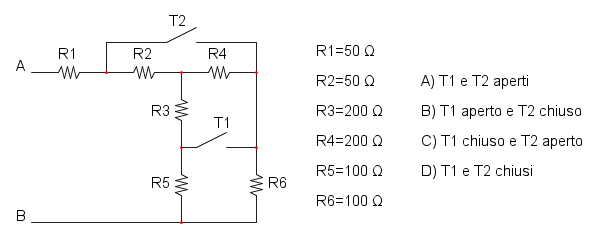
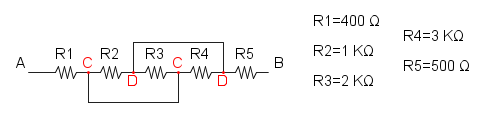
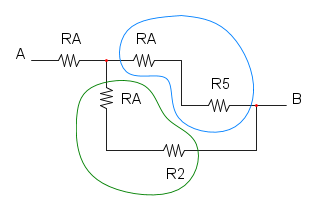
Es.13
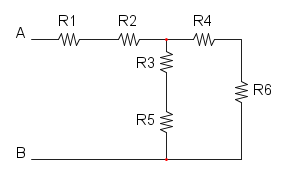
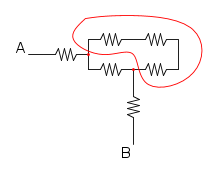
Essendo c e d aperti le resistenze che fuoriesco in quei punti non influenzano il curcuito e pertanto di possono eliminare:
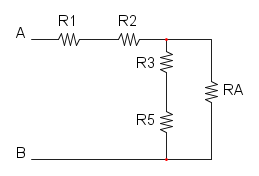
ora le tre resistenze che sono dentro alla curva rossa sono in serie e si possono semplificare:
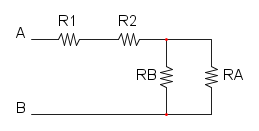
nel cerchio ora ci sono le due resistenze in parallelo:
e per conclure abbiamo le tre resistenze in serie:
![R_{eq}=R+R_B+R=1+\frac{3}{4}+1={\color[RGB]{0,105,50} \frac{11}{4}\ \Omega}](/mediawiki/images/math/f/3/9/f398b5713692c8c4c3d4e90fcbb867ef.png)
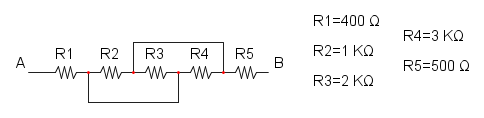
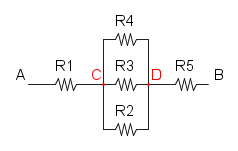
Es.14
anche questo schema non e di facile lettura per cui proviamo a ridisegnarlo:
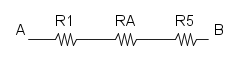
con il nuovo schema si può notare molto più agevolmente che R2, R3 e R4 sono in parallelo:
e per finire abbiamo la serie tra R1, RA e R5:
![R_{eq}=R_1+R_A+R_5=400+545,45+500={\color[RGB]{0,105,50} 1,445\ k\Omega}](/mediawiki/images/math/4/6/4/4644e8c9a9a587f789b4897f5cb6ede6.png)
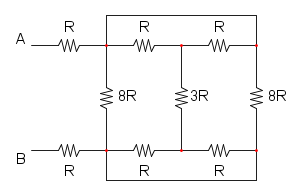
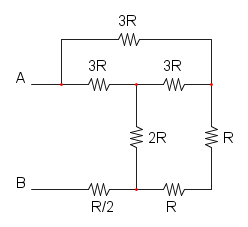
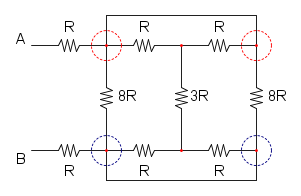
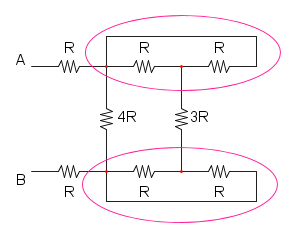
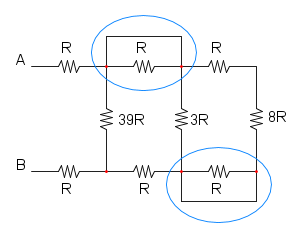
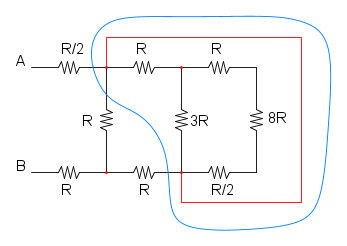
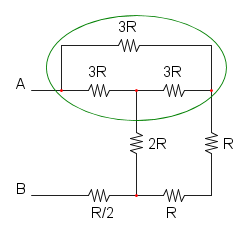
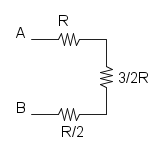
Es.15
Ho cerchiato di rosso i due punti in alto per far capire che si trovano allo stesso potenziale, idem per quelli cerchiati di blu.
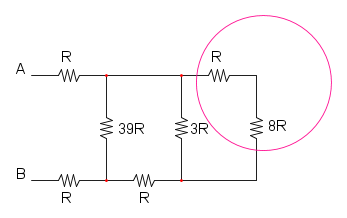
A questo punto si può notare che le due resistenze da 8R sono in parallelo:
RA = 8R / / 8R = 4R
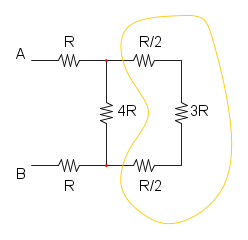
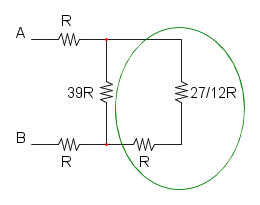
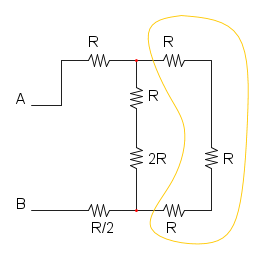
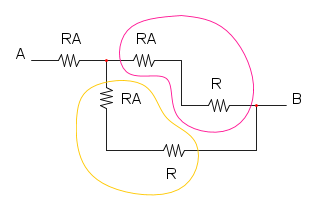
ora possiamo notare che le resistenze nella curva magenta sono in parallelo, sia quelle sopra che quelle sotto:
nella curva gialla abbiamo la serie di tre resistenze:
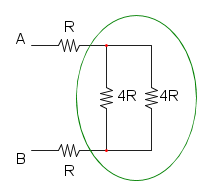
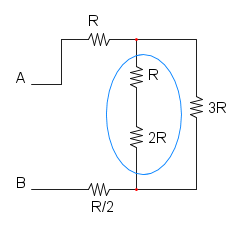
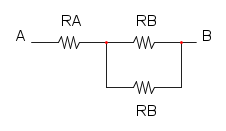
a questo punto semplifichiamo il parallelo:
RD = 4R / / 4R = 2R
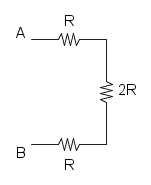
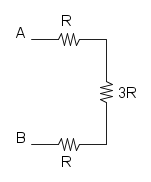
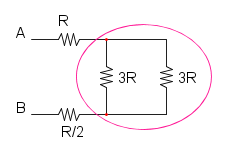
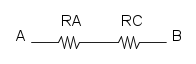
e per finire la sere delle tre resistenze rimaste:
![R_{eq}=R+2R+R={\color[RGB]{0,105,50} 4R}](/mediawiki/images/math/2/e/1/2e1d2f9c88750bc2190c730744bff275.png)
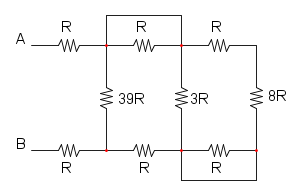
Es.16
possiamo notare che le resistenze all'interno della curva blu sono entrambe in parallelo ad un cortocircuito e per cui si possono eliminare in quanto non influiscono sul circuito:
a questo punto si possono semplificare le resistenze in serie nella curva magenta:
si prosegue con il parallelo delle resistenze indicate nella curva azzurra:
continuiamo con la serie di resistenze nella curva verde:
ora semplifichiamo il parallelo nelle curva gialla:
e per concludere calcoliamo le ultime tre resistenze in serie:
![R_{eq}=R+3R+R={\color[RGB]{0,105,50} 5R}](/mediawiki/images/math/3/9/b/39bdf00c9d698749dc4c9ca6a0120dec.png)
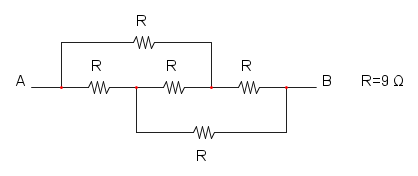
Es.17
Questo esercizio è molto semplice in quanto tutte le resistenze dentro alla curva blu, alla fine riducendole, sono in parallelo ad un cortocircuito (linea di colore rosso) e pertanto sono ininfluenti, quindi lo schema risulterebbe:
possiamo ora semplificare le due resistenze in parallelo all'interno della curva verde:
e per concludere abbiamo la serie delle resistenze rimaste:
![R_{eq}=\frac{R}{2}+\frac{R}{2}+R={\color[RGB]{0,105,50} 2R}](/mediawiki/images/math/5/0/5/505ca19a70b9afc3c05d8e14d3d8ed20.png)
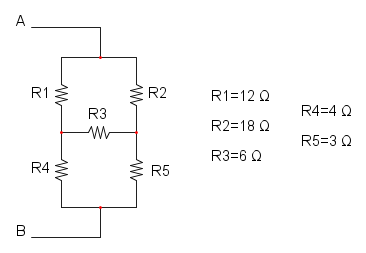
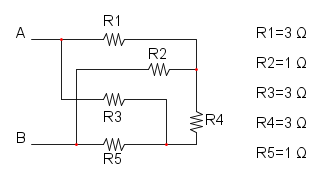
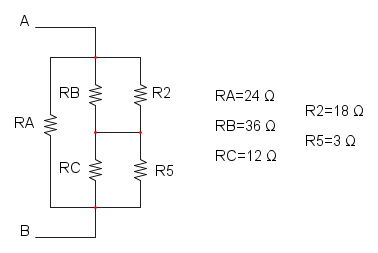
Es. 18
Per risolvere questo tipo di esercizio abbiamo la possibilità di ben 4 casi:
- Con la trasformazione da stella a triangolo di R1, R3 e R4;
- Con la trasformazione da stella a triangolo di R2, R3 e R5;
- Con la trasformazione da triangolo a stella di R1, R2 e R3;
- Con la trasformazione da triangolo a stella di R3, R4 e R5;
Ci sarebbe anche la quinta possibilità che sarebbe l'algebra di Wang che però io non tratterò; se siete interessati potete trovare maggiori informazioni leggendo questo articolo.
Calcoliamo da prima le tre resistenze equivalenti:
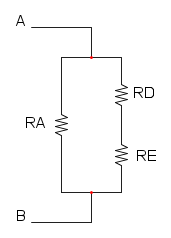
a questo punto ridisegnamo il circuito:
Da qui possiamo semplifichare il parallelo tra RB e R2 e il parallelo tra RC e R5; per cui avremo:
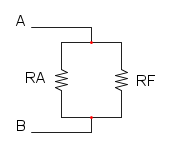
continuiamo con la serie tra RD e RE:
e per finire il parallelo tra RA e RF:
![R_{eq}=R_A//R_F=\frac{24\cdot14,4}{24+14,4}={\color[RGB]{0,105,50}9\ \Omega}](/mediawiki/images/math/b/6/8/b68f2d8fcde9d6c41fd8bbcaace90939.png)
Partiamo sempre a trovare le tre resistenze equivalenti:
ridisegnamo il circuito:
Come prima ora possiamo semplificare il parallelo tra R1 e RB e tra R4 e RC:
ora la serie tra RD e RE:
e per concludere il parallelo tra RF e RA:
![R_{eq}=R_F//R_A=\frac{12,86\cdot30}{12,86+30}={\color[RGB]{0,105,50}9\ \Omega}](/mediawiki/images/math/2/8/3/2837a905b0c94aca523d3a62ff1739ee.png)
Semplifichiamo il triangolo:
e ridisegnamo lo schema:
Ora possiamo semplificare la serie tra RB e R4 e tra RC e R5:
continuiamo col parallelo tra RD e RE:
e per concludere la serie tra RA e RF:
![R_{eq}=R_A+R_F=6+3={\color[RGB]{0,105,50}9\ \Omega}](/mediawiki/images/math/4/7/c/47c5afdc36372b37dba9178fb2abec85.png)
Semplifichiamo il triangolo:
e ridisegnamo lo schema:
ora semplifichiamo la serie tra R1 e RB e tra R2 e RC:
semplifichiamo il parallelo tra RD e RE:
e finiamo con la serie tra RF e RA:
![R_{eq}=R_F+R_A=8,08+0,92={\color[RGB]{0,105,50}9\ \Omega}](/mediawiki/images/math/a/7/4/a7450a30a268a8c5896784809fe86ddb.png)
Es. 19
Anche questo esercizio si potrebbe svolgere in più modi, ossia, trasformando il triangolo formato da R1, R3 e R5; oppure il triangolo formato da R2, R3 e R6; oppure la stella formata da R1, R2 e R3. Noi propenderemo per quest'ultimo caso, perchè se osserviamo le 3 resistenze in questione sono tutte uguali, per cui il calco della trasformazione sarà molto più semplice in quanto ricordo che: RΔ = 3RY, per cui avremo:
e ridisegnamo il circuito:
a questo punto possiamo semplificare i paralleli formati da R5 e RB e da RC e R6:
a questo punto semplifichiamo la serie tra RD e RE:
e per finire facciamo il parallelo delle tre resistenze rimaste R4, RA e RF:
![R{eq}=R_4//R_A//R_F=\frac{1}{\frac{1}{150}+\frac{1}{90}+\frac{1}{112,5}}={\color[RGB]{0,105,50}37,5\ \Omega}](/mediawiki/images/math/5/b/3/5b33d1d5a8d8f79e3d37479e72c86ff6.png)
Es. 20
Anche qui ci sarebbero più modi per risolvere il circuito ma siccome notiamo la presenza di tre resistenze a triangolo tutte uguali andremo a semplificare quelle, così i calcoli saranno più semplici:
semplifichiamo ora le tre resistenze in serie dentro la curva gialla:
RD = R + R + R = 3R
semplifichiamo la serie dentro alla curva blu:
RE = R + 2R = 3R
semplifichiamo il parallelo nella curva magenta:
e per finire la serie delle ultime tre resistenze:
![R_{eq}=R+\frac{3}{2}R+\frac{R}{2}={\color[RGB]{0,105,50}3R}](/mediawiki/images/math/f/2/4/f24d175f07901f245200e82a0e98b3d8.png)
Es. 21
Per comodità trasformiamo uno dei triangoli in stella e avremo:
semplifichiamo le serie che si trovano dentro alle curve che saranno uguali:
ora semplifichiamo il parallelo tra le due resistenze RB:
e per ultimo facciamo la serie tra RA e RC:
![R_{eq}=R_A+R_C=3+6={\color[RGB]{0,105,50}9\ \Omega}](/mediawiki/images/math/2/2/1/221194ff0ebe40c6d1d296918c6669c5.png)
Es. 22
A vederlo sembrerebbe un po complicato, ma proviamo a ridisegnarlo:
possiamo notare che praticamente è uguale all'Es. 21; per cui avendo R1, R3 e R4 che sono uguali trasformeremo quel triangolo in stella:
semplifichiamo le serie nelle curve che sono uguali perchè 
e avremo:
semplifichiamo il parallelo formato dalle RB:
e per finire la serie tra RA e RC:
![R_{eq}=R_A+R_C=1+1={\color[RGB]{0,105,50}2\ \Omega}](/mediawiki/images/math/2/3/6/23614c75c6b4f8b3c4b2e2fcbca08eb7.png)
Es. 23
partiamo con la serie tra R2, R3 e R4:
a questo punto si possono seguire diverse strade perchè ci sono varie stelle o triangoli; io seguirò quello che aveva fatto l'utente di questo esercizio e semplificherò la stella formata da R5, R6 e R7:
ora abbiamo il parallelo tra RA e RC e tra RD e R8:
ora trasformiamo il triangolo formato da RB, RE e RF in stella:
continuiamo con la serie tra R1 e RH, tra RG e R10 e tra RI e R9:
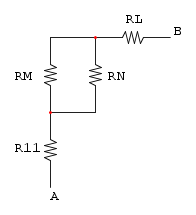
ora il parallelo tra RM e RN:
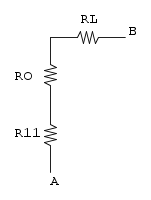
e finiamo con la serie tra R11, RO e RL:
![R_{eq}=R_{11}+R_O+R_L=6+5,9+13,14={\color[RGB]{0,105,50}25.04\ \Omega}](/mediawiki/images/math/7/5/6/756d48c04f933eaafeed186395df74f5.png)
