Introduzione
Una recente domanda sul forum riguardava il calcolo dell'impedenza vista guardando dentro l'emettitore di un transistore bipolare in linearità, in particolare si voleva conoscere un modo rigoroso di calcolare questa impedenza.
La mia risposta era stata breve, indicando solo un possibile metodo di calcolo, anche se avevo detto che ve n'erano parecchi possibili.
In questo articoletto saranno presentati vari metodi di calcolo delle impedenze, alcuni ben noti e comuni, mentre altri sono meno diffusi e si spera di contribuire a diffonderli. In realtà questo intervento è solo una scusa per ripassare alcuni metodi per calcolare impedenze varie. Saranno solo presentate le procedure di calcolo, senza approfondire le dimostrazioni.
Il circuito usato per illustrare i vari procedimenti di calcolo è così semplice che in alcuni casi diventa difficile applicare qualche metodo "avanzato" perché ogni cambiamento fatto al circuito per applicare il metodo snatura o distrugge il circuito. Si cercherà comunque di usare in modo rigoroso la citata "mezza dozzina" di metodi per trovare l'impedenza.
Circuito di riferimento
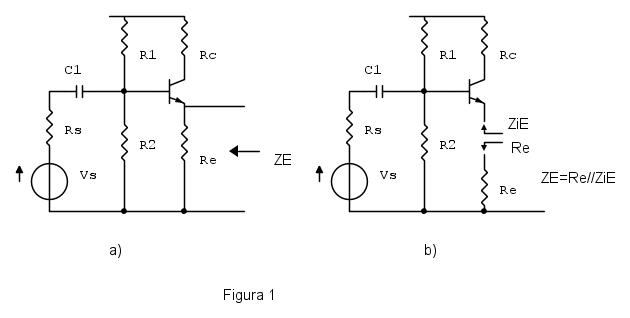
Il circuito originale cui si faceva riferimento è quello di figura 1a in cui si voleva sapere l'impedenza  . Molto spesso èconveniente fare il conto come indicato in figura 1b, considerando il parallelo fra
. Molto spesso èconveniente fare il conto come indicato in figura 1b, considerando il parallelo fra  e
e  e calcolando separatamente
e calcolando separatamente  .
.
Nel seguito il transistore sarà modellato con il suo equivalente a pi greco ibrido [1], usando solo i parametri  e
e  . si assumerà che il transistore non presenti effetto Early, quindi la resistenza
. si assumerà che il transistore non presenti effetto Early, quindi la resistenza  ha valore infinito, e di lavorare a bassa frequenza, quindi le capacità parassite del transistore, che danno una limitazione in alta frequenza alla banda di funzionamento, non intervengono.
ha valore infinito, e di lavorare a bassa frequenza, quindi le capacità parassite del transistore, che danno una limitazione in alta frequenza alla banda di funzionamento, non intervengono.
Per semplificare i conti si fa un equivalente Thévenin di tutta la parte di ingresso del circuito, che quindi si riduce all'impedenza equivalente

e al generatore equivalente  il cui valore non è importante, dovendo calcolare una impedenza. Si omette di disegnare la resistenza
il cui valore non è importante, dovendo calcolare una impedenza. Si omette di disegnare la resistenza  che in assenza di effetto Early non dà effetti sull'impedenza di emettitore, e quando possibile si calcola direttamente
che in assenza di effetto Early non dà effetti sull'impedenza di emettitore, e quando possibile si calcola direttamente  , valutando successivamente il parallelo con
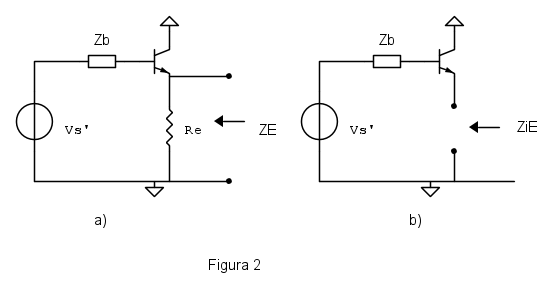
, valutando successivamente il parallelo con  . I due circuiti di riferimento saranno quindi quelli di figura 2.
. I due circuiti di riferimento saranno quindi quelli di figura 2.
Il valore dell'impedenza  è una espressione ben conosciuta che si trova su tutti i libri e vale
è una espressione ben conosciuta che si trova su tutti i libri e vale

mentre l'impedenza  complessiva vale ovviamente
complessiva vale ovviamente

Da notare che è sbagliato scrivere

o peggio ancora scrivere ad esempio

L'ultima espressione, ancorché corretta, va tuttavia evitata poiché è illeggibile, non fornisce indicazioni sul circuito che si sta studiando. Stesso discorso per l'espressione (3), anche lei non è una espressione a bassa entropia [2][3].
Metodi di calcolo
I metodi di calcolo dell'impedenza illustrati e commentati nel seguito, ma non dimostrati, sono i seguenti, dove è indicato l'anno della definizione del metodo oppure la sua prima pubblicazione.
- Generatori di prova
- Tensione a vuoto e corrente di cortocircuito
- Metodo dei nodi
- Formula di Blackman (1943)
- Teorema delle impedenze (<1988)
- Metodo dell'elemento aggiunto (<1988)
- Metodo Rosenstark (1974)
- Teorema di Scomposizione (1972)
- General Feedback Theorem (2001)
- E Miller? (1920)
Da notare che la lista non è esaustiva, ma direi che rappresenti i metodi più utilizzati.
I primi metodi della lista sono di estrazione elettrotecnica. A partire dalla formula di Blackmnan si inizia con i metodi "elettronici", in cui spesso la retroazione compare in modo evidente. Nella sezione dedicata al General Feedback Theorem viene anche mostrato che molti dei metodi elettronici sono tra di loro equivalenti e derivabili uno dall'altro.
Purtroppo a causa della topologia del circuito, alcuni metodi non sono applicabili, come ad esempio i teoremi di Miller, mentre la semplicità del circuito rende difficoltoso o non conveniente usare delle estensioni dei precedenti metodi, ad esempio la sovrapposizione degli effetti usata in concomitanza ad esempio con i generatori di prova.
Altre possibili strade per il calcolo dell'impedenza di emettitore, come ad esempio l'utilizzo del modello a T del transistore, o il modello con la transconduttanza, oppure ancora metodi più astratti, come l'utilizzo delle matrici dei doppi bipoli, saranno altresì tralasciati.
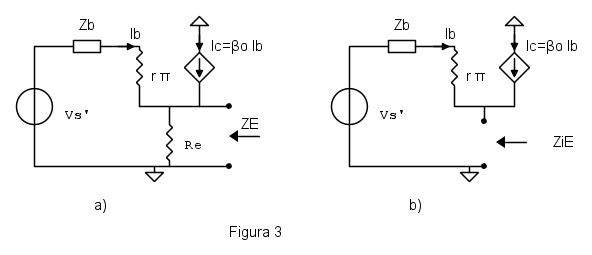
Il circuito equivalente su cui si lavorerà è mostrato in figura 3, al solito si cercherà di lavorare sul circuito 3b, ma in qualche caso potrebbe essere necessario includere la resistenza di emettitore fin dall'inizio dei calcoli.
Il generatore di ingresso  è ancora indicato, anche se molto spesso dovrà essere spento.
è ancora indicato, anche se molto spesso dovrà essere spento.
Il solo metodo che è praticamente mai applicabile in presenza di generatori pilotati, è la valutazione a vista, o by inspection dell'impedenza. Procedendo a vista quasi certamente si commettono errori grossolani. Ad esempio si potrebbe essere tentati di dire che  dimenticando l'effetto del generatore pilotato e ottenendo un risultato totalmente errato.
dimenticando l'effetto del generatore pilotato e ottenendo un risultato totalmente errato.
Generatori di prova
In questo caso è possibile calcolare da subito  perciò si aggiungerà la resistenza
perciò si aggiungerà la resistenza  solo alla fine.
solo alla fine.
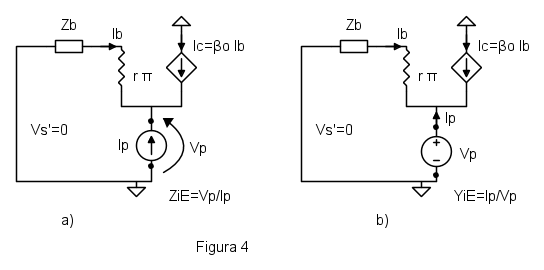
Il metodo con i generatori di prova applica la definizione di impedenza o di ammettenza. Si spengono tutti i generatori indipendenti e si applica ai morsetti sui quali si vuole trovare l'impedenza un generatore di corrente di prova  calcolando la tensione
calcolando la tensione  che si localizza ai suoi capi. Il rapporto
che si localizza ai suoi capi. Il rapporto  fornisce l'impedenza cercata, figura 4a.
fornisce l'impedenza cercata, figura 4a.
Da osservare che anche l'impedenza è una funzione di trasferimento, dove l'ingresso è la corrente applicata e l'uscita la tensione che si localizza agli stessi morsetti.
Se invece si usa un generatore di prova di tensione  , sempre dopo aver spento tutti i generatori indipendenti, si calcola la corrente
, sempre dopo aver spento tutti i generatori indipendenti, si calcola la corrente  che esce dal generatore, figura 4b. In questo caso l'ingresso alla funzione di trasferimento è la tensione e l'uscita è la corrente e quindi il rapporto uscita/ingresso fornisce
che esce dal generatore, figura 4b. In questo caso l'ingresso alla funzione di trasferimento è la tensione e l'uscita è la corrente e quindi il rapporto uscita/ingresso fornisce  l'ammettenza vista ai due morsetti. Ovviamente
l'ammettenza vista ai due morsetti. Ovviamente  e quindi si può calcolare indifferentemente Z o Y a seconda di quale sia più comoda.
e quindi si può calcolare indifferentemente Z o Y a seconda di quale sia più comoda.
Generatore di corrente
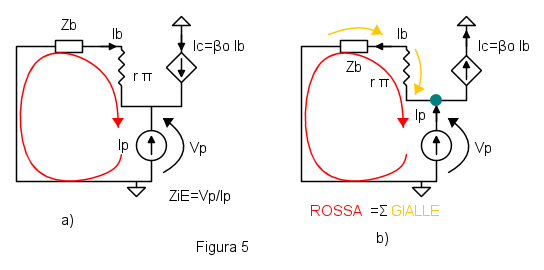
Per trovare la tensione ai capi del generatore di corrente di prova bisogna usare una maglia di tensioni che non passi per il generatore di corrente controllato, altrimenti avremmo una tensione incognita in più. La maglia da utilizzarsi è in figura 5a, dalla quale si riesce a calcolare la tensione ai capi del generatore di corrente  che è pari alla caduta tensione su
che è pari alla caduta tensione su  più quella su
più quella su  . Questa è la solita legge di Kirchhoff per le tensioni, e si potrebbe scrivere facilmente la tensione in funzione della corrente di base
. Questa è la solita legge di Kirchhoff per le tensioni, e si potrebbe scrivere facilmente la tensione in funzione della corrente di base  .
.
Però a me non piace molto scrivere tante equazioni, soprattutto se la corrente di base  va al contrario rispetto a quanto ci farebbe comodo. Può essere più conveniente girare i versi delle correnti
va al contrario rispetto a quanto ci farebbe comodo. Può essere più conveniente girare i versi delle correnti  e
e  in modo da eliminare segni negativi e vedere le tensioni che si sommano con le correnti che scorrono nel verso "giusto", come mostrato in figura 5b.
in modo da eliminare segni negativi e vedere le tensioni che si sommano con le correnti che scorrono nel verso "giusto", come mostrato in figura 5b.
Per trovare la corrente  si lavora sul nodo di emettitore (pallino verde) e si vede che
si lavora sul nodo di emettitore (pallino verde) e si vede che

da cui con arditi passaggi matematici si ha che

da cui infine si ricava
 .
.
Dato che dobbiamo trovare l'impedenza, il passaggio finale è

e come è giusto che sia  si semplifica, anzi deve proprio capitare, il risultato non deve contenere nessun generatore! Il risultato che si trova è quindi lo stesso indicato in (1)
si semplifica, anzi deve proprio capitare, il risultato non deve contenere nessun generatore! Il risultato che si trova è quindi lo stesso indicato in (1)

Generatore di tensione
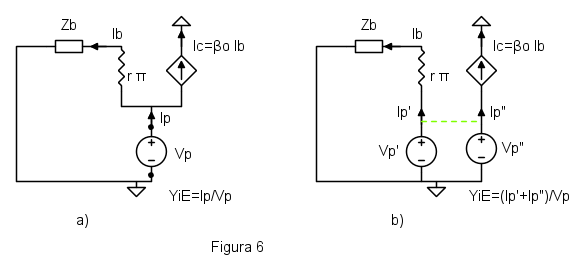
L'analisi con il generatore di tensione è analoga: si mette un generatore di prova di tensione  ai morsetti sui quali si vuole trovare l'impedenza e si spengono tutti gli altri generatori indipendenti. Si calcola la corrente che esce dal positivo del generatore di tensione e il rapporto dà l'ammettenza ai morsetti, come mostrato in figura 6a, dove si è provveduto a girare i segni delle correnti.
ai morsetti sui quali si vuole trovare l'impedenza e si spengono tutti gli altri generatori indipendenti. Si calcola la corrente che esce dal positivo del generatore di tensione e il rapporto dà l'ammettenza ai morsetti, come mostrato in figura 6a, dove si è provveduto a girare i segni delle correnti.
I teorici dell'elettrotecnica i dispositivisti elettronici et similia usano sempre la convenzione delle correnti entrante positiva. Anche sui data sheet si usa la stessa convenzione, ma facendo i conti forse è meglio usare una convenzione con il minor numero possibile di segni negativi, si riduce di molto la probabilità di errore, come dice anche pietrobaima ad esempio qui.
La corrente di base  la si calcola direttamente osservando che
la si calcola direttamente osservando che  e
e  sono in serie e la corrente di base vale quindi
sono in serie e la corrente di base vale quindi

La corrente di emettitore, che è anche  vale quella di base più quella di collettore pari a
vale quella di base più quella di collettore pari a  volte quella di base, per cui la corrente
volte quella di base, per cui la corrente  risulta essere
risulta essere

e quindi l'ammettenza guardando dentro l'emettitore del transistore vale

e infine l'impedenza di ingresso vale, come era già stato calcolato prima

Al solito il valore del generatore di prova si semplifica e non compare nel risultato.
Split del generatore
Quando si calcola l'impedenza di un nodo rispetto al riferimento, come in questo caso, spesso è conveniente suddividere il generatore di tensione di prova  in tanti generatori uguali, collegati ciascuno a un ramo che converge nel nodo [4]. Tutti i generatori generano la stessa tensione
in tanti generatori uguali, collegati ciascuno a un ramo che converge nel nodo [4]. Tutti i generatori generano la stessa tensione  , ma può essere opportuno usare nomi diversi, ad esempio
, ma può essere opportuno usare nomi diversi, ad esempio  ,
,  ...
...
Dopo aver fatto questa suddivisione, come indicato in figura 6b, si utilizza la sovrapposizione degli effetti accendendo un solo generatore per volta e sommando tutti i contributi di corrente. In generale, con un generatore iniziale  suddiviso in
suddiviso in  generatori separati, potrebbero esserci
generatori separati, potrebbero esserci  contributi di corrente, ma di solito sono molti di meno.
contributi di corrente, ma di solito sono molti di meno.
Nel caso di figura 6b l'ammettenza è data da

dove la sommatoria tiene conto di tutti i contributi. In linea di principio si potrebbero avere 4 correnti in questo modo

In questo esempio i contributi  e
e  sono nulli e rimangono solo
sono nulli e rimangono solo
 e
e

sommando i quali si ottiene l'identico risultato di prima.
In questo caso il metodo della suddivisione del generatore non porta ad alcun vantaggio, ma in circuiti più complicati può risultare molto utile.
Tensione a vuoto e corrente di cortocircuito
Se lasciando attivo un generatore indipendente della rete si riesce a calcolare la tensione a vuoto  fra due morsetti e la corrente di cortocircuito
fra due morsetti e la corrente di cortocircuito  fra gli stessi due morsetti, allora l'impedenza di uscita o di entrata (sono la stessa cosa!) fra quei due morsetti è data da
fra gli stessi due morsetti, allora l'impedenza di uscita o di entrata (sono la stessa cosa!) fra quei due morsetti è data da

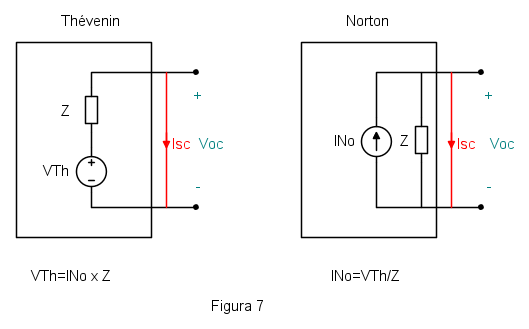
I pedici oc e sc indicano Open Circuit e Short Circuit. La (10) è una ovvia conseguenza se si osservano gli equivalenti Thévenin e Norton a due morsetti della stessa rete, indicata in figura 7.
Sia che si lavori sulla rete di sinistra che su quella di destra, il rapporto fra tensione a vuoto divisa per la corrente di cortocircuito dà sempre  : non per nulla si chiamano equivalenti!
: non per nulla si chiamano equivalenti!
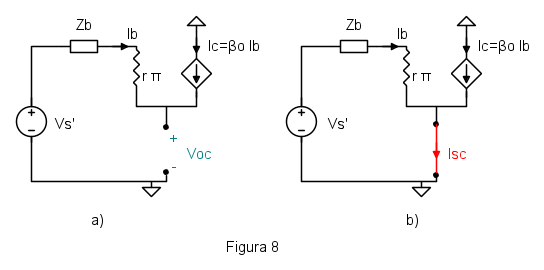
Nel caso del transistore si può calcolare la tensione a vuoto e la corrente di cortocircuito escludendo dal calcolo la resistenza di emettitore  , lasciando attivo il generatore di ingresso
, lasciando attivo il generatore di ingresso  e calcolando le due grandezze, come mostrato in figura 8.
e calcolando le due grandezze, come mostrato in figura 8.
Il calcolo della tensione a vuoto  è immediato. Essendo l'emettitore non collegato a nulla, la corrente di collettore deve essere opposta a quella di base, ovvero
è immediato. Essendo l'emettitore non collegato a nulla, la corrente di collettore deve essere opposta a quella di base, ovvero

Essendo  l'unica soluzione di (18) è
l'unica soluzione di (18) è  . Essendo la corrente di base nulla, non vi è caduta di tensione lungo
. Essendo la corrente di base nulla, non vi è caduta di tensione lungo  e quindi la tensione di emettitore e quindi la vuoto vale
e quindi la tensione di emettitore e quindi la vuoto vale

Se fosse stata presente la resistenza di emettitore il conto sarebbe stato più lungo.
il conto sarebbe stato più lungo.
Per valutare la corrente di cortocircuito si osserva che  ed
ed  sono in serie e ai loro capi vi è la tensione
sono in serie e ai loro capi vi è la tensione  , quindi la corrente di base vale
, quindi la corrente di base vale  . La corrente di cortocircuito
. La corrente di cortocircuito  è data dalla somma di
è data dalla somma di  e quindi si ha
e quindi si ha

e infine dividendo la (19) per la (20) si ottiene

che è ancora l'espressione (1). Al solito il generatore indipendente lasciato nel circuito si semplifica e il risultato non dipende dall'ampiezza del segnale. In questo caso il segnale che eccita la rete è il normale ingresso del circuito, e anche lui deve semplificarsi, dato che il risultato è una funzione di trasferimento.
Questo metodo viene più spesso usato per calcolare la tensione di uscita dell'amplificazione e quindi l'amplificazione di un circuito, valutando separatamente l'impedenza di uscita  e la corrente di cortocircuito
e la corrente di cortocircuito  e trovando la tensione di uscita come
e trovando la tensione di uscita come  come spiegato in [5] e [6].
come spiegato in [5] e [6].
Metodo dei nodi
Prima di abbandonare la sezione dei metodi elettrotecnici, viene presentato un metodo formale e astratto per il calcolo dell'impedenza, metodo basato su matrici e determinanti. Il metodo dei nodi o dei potenziali ai nodi [10] è molto generale e viene usato per l'analisi con calcolatore dei circuiti, permettendo di calcolare qualunque grandezza di rete (amplificazioni, impedenze...). Il suo uso a mano è spesso molto laborioso, confesso di averlo usato qualche volta per trovare delle funzioni di trasferimento, ma non mi pare di averlo mai usato per trovare una impedenza!
L'idea base del metodo dei nodi consiste nello scrivere le equazioni di funzionamento del circuito usando come incognite i potenziali dei vari nodi, e come termini noti si usano le correnti dei generatori di ingresso. Se ci sono dei generatori di tensione bisogna cercare di rappresentarli come equivalenti Norton, oppure si introduce una incognita in più. I generatori pilotati di corrente devono avere il pilota dato dal potenziale a un nodo o dalla differenza di potenziale fra due nodi.
Infine se si fanno conti algebrici è opportuno scrivere tutti gli elementi della rete sotto forma di ammettenze, a meno di non volersi complicare la vita con espressioni del tipo 1/R.
Il circuito di figura 9 è il solito circuito preparato per l'analisi con il metodo dei nodi. Il segnale di ingresso è stato trasformato in generatore di corrente e il generatore pilotato è ora comandato dalla tensione  e la sua amplificazione vale
e la sua amplificazione vale  .
.
Il sistema matriciale  che descrive il circuito, dove
che descrive il circuito, dove  è la matrice delle ammettenza si può scrivere a vista, se si conosce la tecnica delle conduttanze direzionali, altrimenti bisogna fare un po' di algebra. I segni delle correnti vengono presi positivi uscenti da ciascun nodo, anche per il generatore pilotato, la cui grandezza pilota dovrà essere scritta in modo coerente con questa convenzione.
è la matrice delle ammettenza si può scrivere a vista, se si conosce la tecnica delle conduttanze direzionali, altrimenti bisogna fare un po' di algebra. I segni delle correnti vengono presi positivi uscenti da ciascun nodo, anche per il generatore pilotato, la cui grandezza pilota dovrà essere scritta in modo coerente con questa convenzione.
In entrambi i casi sulla diagonale principale della matrice delle ammettenze, termini  c'è la somma delle ammettenze che partono da ogni nodo, mentre sui termini fuori diagonale
c'è la somma delle ammettenze che partono da ogni nodo, mentre sui termini fuori diagonale  c'è, con il segno negativo, la somma delle ammettenze che collegano i due nodi i e j. Inoltre nella matrice sono presenti i termini dovuti al generatore pilotato.
c'è, con il segno negativo, la somma delle ammettenze che collegano i due nodi i e j. Inoltre nella matrice sono presenti i termini dovuti al generatore pilotato.

Poiché si cerca solo l'impedenza sul nodo di emettitore, si lavora solo sulla matrice delle ammettenze e l'impedenza cercata vale

dove  è il determinante della matrice delle ammettenze, e
è il determinante della matrice delle ammettenze, e  è il complemento algebrico della matrice delle ammettenze, avendo rimosso la seconda riga e la seconda colonna, dato che si vuole trovare l'impedenza sul nodo 2,
è il complemento algebrico della matrice delle ammettenze, avendo rimosso la seconda riga e la seconda colonna, dato che si vuole trovare l'impedenza sul nodo 2,  , rispetto al riferimento. Sviluppando i determinanti (quello a numeratore è un termine singolo!) si ottiene
, rispetto al riferimento. Sviluppando i determinanti (quello a numeratore è un termine singolo!) si ottiene

e risostituendo le ammettenze con le corrispondenti impedenze si ha

Stesso risultato di prima ottenuto con un lavoro di una noia suprema!
Formula di Blackman
Con la formula di Blackman usciamo dai metodi dell'elettrotecnica ed entriamo in quello dei circuiti elettronici retroazionati. Questi circuiti sono solitamente difficili da analizzare poiché richiedono la soluzione di sistemi di equazioni dato che il generatore pilotato ha la grandezza pilota che dipende dal generatore stesso. Il metodo di Blackman [7][8] permette di togliere questa dipendenza (aprire l'anello di retroazione) e i conti diventano decisamente più semplici. Anche se storicamente la formula di Blackman è venuta una trentina d'anni prima del metodo di Rosenstark [13a][13b], tuttavia Blackman è una particolare derivazione di Rosenstark, anche se quest'ultimo non ha mai notato questa derivazione.
L'impedenza fra due morsetti, in questo caso ZiE calcolata secondo Blackman richiede di identificare un componente, tipicamente un generatore pilotato che si trovi dentro l'anello di retroazione, e vale

dove  è l'impedenza vista fra i due morsetti a sistema morto (Dead), vale a dire con il generatore pilotato scelto annullato, messo con guadagno nullo. Le grandezze
è l'impedenza vista fra i due morsetti a sistema morto (Dead), vale a dire con il generatore pilotato scelto annullato, messo con guadagno nullo. Le grandezze  e
e  sono i rapporti di ritorno (anche chiamati meno correttamente guadagni di anello) calcolati rispetto al generatore pilotato scelto e con i morsetti sui quali si vuole trovare l'impedenza in cortocircuito oppure in circuito aperto.
sono i rapporti di ritorno (anche chiamati meno correttamente guadagni di anello) calcolati rispetto al generatore pilotato scelto e con i morsetti sui quali si vuole trovare l'impedenza in cortocircuito oppure in circuito aperto.
Calcolo di 
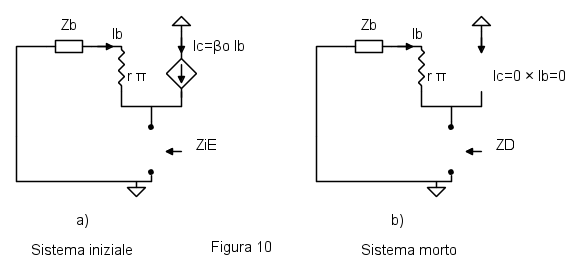
Nel caso dell'impedenza di emettitore vi è un solo generatore pilotato, sul quale si faranno le varie operazioni. Il primo passo consiste nello spegnere il generatore pilotato e calcolare l'impedenza vista dai morsetti sui quali si vuole l'impedenza finale. In figura 10a è rappresentato il circuito iniziale e in 10b la trasformazione per trovare l'impedenza a sistema morto 
Da ricordare che annullare il generatore pilotato significa mettere il suo guadagno a zero, quindi un generatore di corrente si trasforma in un circuito aperto. L'operazione di annullamento è una operazione "elettrotecnica" fatta solo sul generatore pilotato. Non si manda a zero il  del transistore, che farebbe cambiare anche
del transistore, che farebbe cambiare anche  , si manda a zero solo il guadagno del generatore, la resistenza
, si manda a zero solo il guadagno del generatore, la resistenza  ed eventualmente tutti gli altri parametri che dipendono dal guadagno
ed eventualmente tutti gli altri parametri che dipendono dal guadagno  rimangono invariati: si lavora sul generatore pilotato, non sul modello del transistore.
rimangono invariati: si lavora sul generatore pilotato, non sul modello del transistore.
L'impedenza a sistema morto viene valutata a vista poiché non ci sono più generatori pilotati e vale ovviamente

Calcolo dei rapporti di ritorno 
Il calcolo del rapporto di ritorno  viene fatto seguendo queste semplici passi
viene fatto seguendo queste semplici passi
- Si rimuove dal circuito il generatore pilotato, lasciandolo scollegato dal circuito
- Al posto del generatore pilotato si mette un generatore di prova
 dello stesso tipo e con la stessa polarità del generatore pilotato che è stato messo da parte
dello stesso tipo e con la stessa polarità del generatore pilotato che è stato messo da parte
- Si calcola l'eccitazione sul pilota del generatore pilotato causata dal generatore di prova
- Si calcola l'uscita del generatore pilotato
 provocata dal generatore di prova.
provocata dal generatore di prova.
- Il rapporto di ritorno vale

Il calcolo deve essere ripetuto due volte, una con i morsetti in circuito aperto e una in cortocircuito. Spesso uno dei due rapporti di ritorno è nullo.
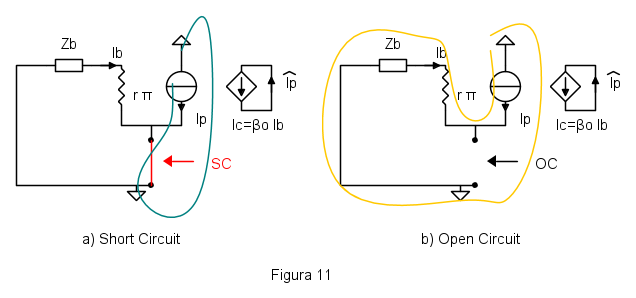
I due circuiti per il calcolo dei rapporti di ritorno sono mostrati in figura 11. Il generatore di corrente del modello del transistore è stato rimosso e collegato in cortocircuito, altrimenti un generatore di corrente in circuito aperto è fortemente infelice! Il generatore pilotato è ancora comandato dalla corrente  , che deve essere valutata in funzione della corrente di prova
, che deve essere valutata in funzione della corrente di prova  . Da notare che il generatore di prova è di corrente e spinge la corrente nello stesso verso (convenzionale) del generatore pilotato originale.
. Da notare che il generatore di prova è di corrente e spinge la corrente nello stesso verso (convenzionale) del generatore pilotato originale.
Nel caso in cui si cortocircuitano i morsetti sui quali si vuole trovare l'impedenza (figura 11a), il generatore di prova non riesce a far scorrere alcuna corrente di base. Si ha quindi

da cui si ricava il rapporto di ritorno in cortocircuito

Il conto di  viene fatto considerando il circuito di destra, figura 11b. In questo caso il generatore di prova riesce a far scorrere una corrente di pilotaggio, e si vede che
viene fatto considerando il circuito di destra, figura 11b. In questo caso il generatore di prova riesce a far scorrere una corrente di pilotaggio, e si vede che

Nel calcolo del rapporto di ritorno un segno negativo è inevitabile! La corrente di base Ib fa scorrere una corrente di collettore  e quindi di può scrivere il rapporto di ritorno a circuito aperto:
e quindi di può scrivere il rapporto di ritorno a circuito aperto:

Se anche questo rapporto di ritorno fosse stato nullo, avrebbe significato che il circuito non è reazionato. Se entrambi fossero stati diversi da zero ed uguali, avrebbe significato che l'impedenza che si sta cercando è al di fuori dell'anello di retroazione. Infine se uno dei due rapporti di ritorno è nullo, come in questo caso, vuol dire che la retroazione per quanto riguarda quei morsetti è di tipo parallelo se  mentre è di tipo serie se si ha
mentre è di tipo serie se si ha  .
.
Finalmente possiamo trovare l'impedenza di emettitore usando le formule (26), (27), (29) e (31):

Ancora lo stesso risultato! (e per fortuna!)
Teorema delle Impedenze
Il teorema delle impedenze di ingresso e di uscita [9] è una astuta applicazione del metodo della tensione a vuoto e corrente di cortocircuito presentato prima. Per applicarlo si suppone di avere a disposizione l'espressione dell'amplificazione del circuito. In effetti spesso per analizzare un amplificatore bisogna calcolarne l'amplificazione e le impedenze.
Al posto di calcolare separatamente la tensione a vuoto e la corrente di cortocircuito, come mostrato in precedenza, si fa uso dell'espressione dell'amplificazione, calcolando dei semplici limiti di espressioni in cui compare l'amplificazione calcolata precedentemente.
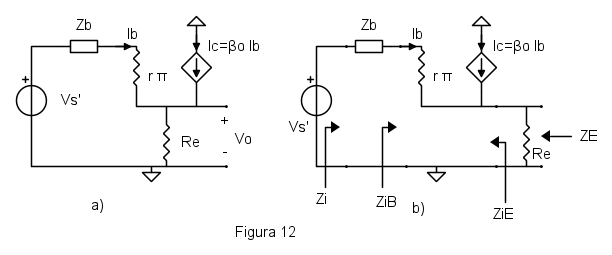
Supponiamo di aver calcolato per il circuito di figura 12a l'amplificazione di tensione  .
.
L'amplificazione di questo transistore connesso a collettore comune vale

e come c'era da aspettarsi è poco minore di 1, specie se la resistenza di emettitore cade in continua una tensione molto maggiore dell'equivalente in tensione della temperatura  .
.
Teorema dell'impedenza di uscita
La derivazione del teorema dell'impedenza di uscita è semplice. Se si vuole calcolare l'impedenza  usando la tensione a vuoto e la corrente di cortocircuito si ha che la tensione a vuoto vale
usando la tensione a vuoto e la corrente di cortocircuito si ha che la tensione a vuoto vale

Tensione a vuoto in questo caso vuol dire la tensione sull'uscita senza collegare nient'altro all'uscita tranne  che è già presente nel circuito.
che è già presente nel circuito.
La corrente di uscita (non ancora quella di cortocircuito) è data dalla tensione di uscita diviso per la resistenza  e vale
e vale

Se si vuole il valore della corrente di cortocircuito basta prendere il limite per  e si ha che
e si ha che

Dividendo la (34) per la (35) si ottiene l'impedenza "esterna", che include il valore della resistenza di carico  :
:

Se si vuole il valore di  , come calcolato in precedenza, basta calcolare la tensione a vuoto senza la resistenza
, come calcolato in precedenza, basta calcolare la tensione a vuoto senza la resistenza  quindi mandandola ad infinito e si ottiene
quindi mandandola ad infinito e si ottiene

Le (37) e (38) costituiscono il teorema delle impedenze di uscita. Applicando ad esempio la (37) al circuito di figura 12, con il guadagno (33) si ha

Evviva! Ancora una volta si è ottenuto lo stesso risultato!
Teorema dell'impedenza di ingresso
Avendo l'espressione dell'amplificazione, si può facilmente calcolare l'impedenza di ingresso, con un modo analogo al precedente. Senza stare a ricavarlo si hanno per le due impedenze  (impedenza esterna) e
(impedenza esterna) e  (impedenza interna) le seguenti espressioni (teorema delle impedenze di ingresso)
(impedenza interna) le seguenti espressioni (teorema delle impedenze di ingresso)


Anche in questo caso l'applicazione è semplice, i limiti si semplificano facilmente. Provando a valutare l'impedenza interna  si ottiene
si ottiene

Teorema dell'elemento aggiunto
Il teorema dell'elemento aggiunto, o Extra Element Theorem (EET), è un altro regalo del prof. Middlebrook [11][12]. Scherzando potrebbe anche essere chiamato il teorema per l'ingegnere distratto perché consente di fare tutti i conti su una rete senza un elemento, poi, essendosi accorti di aver dimenticato un componente, lo si può aggiungere alla rete senza dover rifare i conti da capo, ma usando il risultato trovato moltiplicato per un fattore correttivo.
In realtà questo teorema viene usato eliminando dal circuito un componente che la rende "difficile", si risolve la rete semplificata infine si aggiunge l'effetto del componente che si era tolto. L'operazione può essere essere fatta sulle funzioni di trasferimento che sulle impedenze, che tutto sommato sono anche loro funzioni di trasferimento fra tensione e corrente agli stessi morsetti.
Il teorema si presenta in due versioni, in cui si aggiunge una impedenza extra in parallelo fra due nodi, oppure in cui si inserisce una impedenza extra in serie a un collegamento, in pratica si "taglia un filo" e si aggiunge una impedenza in serie.
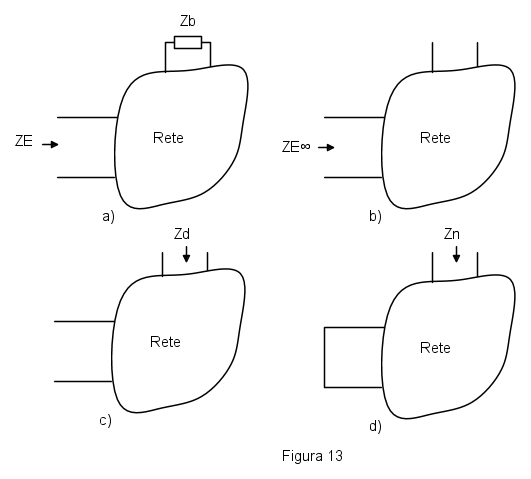
Per applicare questo teorema alle impedenze si segue la procedura di figura 13. Si vuole trovare l'impedenza  fra due morsetti di una rete che comprende anche l'impedenza
fra due morsetti di una rete che comprende anche l'impedenza  (uso già i nomi effettivi della rete su cui poi si faranno i conti), figura 13a. Come operazione preliminare si eliminano tutti i generatori indipendenti di segnale. Il primo passo consiste nel togliere l'impedenza "rompiscatole" e nel calcolare l'impedenza
(uso già i nomi effettivi della rete su cui poi si faranno i conti), figura 13a. Come operazione preliminare si eliminano tutti i generatori indipendenti di segnale. Il primo passo consiste nel togliere l'impedenza "rompiscatole" e nel calcolare l'impedenza  che si vede dai morsetti avendo tolto l'impedenza
che si vede dai morsetti avendo tolto l'impedenza  , come mostrato in figura 13b
, come mostrato in figura 13b
I due passi successivi consistono del trovare le impedenze  e
e  che sono le impedenze viste dai morsetti dove sarà collegata
che sono le impedenze viste dai morsetti dove sarà collegata  , quando i morsetti sui quali si vuole l'impedenza sono in circuito aperto (figura 13c) e in cortocircuito (figura 13d). Dopo aver trovato questi tre parametri si può trovare l'impedenza cercata con questa relazione
, quando i morsetti sui quali si vuole l'impedenza sono in circuito aperto (figura 13c) e in cortocircuito (figura 13d). Dopo aver trovato questi tre parametri si può trovare l'impedenza cercata con questa relazione

L'uso dell'EET sembrerebbe un pessimo affare: per trovare una impedenza se ne devono calcolare altre tre! In realtà il conto delle tre impedenze è normalmente molto più facile rispetto al calcolo di quella iniziale.
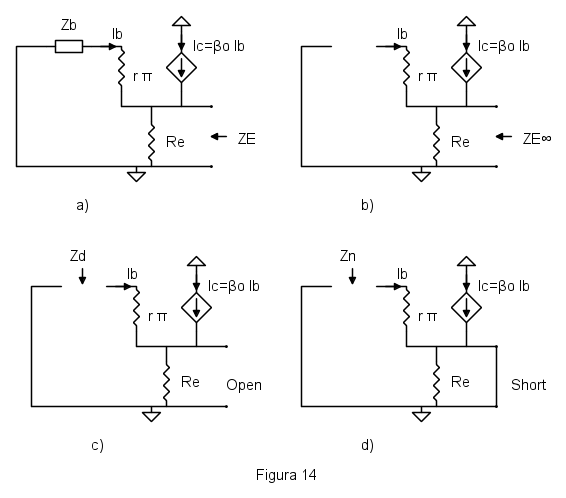
Applicazione del teorema dell'elemento aggiunto
L'uso del teorema dell'elemento aggiunto sul circuito di questo articolo non è la cosa più astuta, perché il circuito è molto semplice e se si toglie un componente si snatura il circuito. Però, for the sake of completness, ci si può provare. L'impedenza che viene tolta, per poi essere aggiunta alla fine, è  , e l'analisi deve essere fatta con la resistenza
, e l'analisi deve essere fatta con la resistenza  presente, altrimenti si hanno delle grandezze che vanno a infinito.
presente, altrimenti si hanno delle grandezze che vanno a infinito.
I vari circuiti, iniziale e per la valutazione delle varie impedenze, sono in figura 14.
L'impedenza  è immediata guardando figura 14b. Dato che avendo tolto
è immediata guardando figura 14b. Dato che avendo tolto  nella base non passa più corrente, l'impendenza che si vede guardando nell'emettitore vale
nella base non passa più corrente, l'impendenza che si vede guardando nell'emettitore vale

L'impedenza  è quella solita vista guardando nella base di un transistore. Qui devo barare un pochino, supponendo di conoscerla. Nei circuiti reali e più complicati le impedenze da calcolare in itinere sono più semplici di quella cercata. L'impedenza di ingresso guardando nella base di un transistore vale
è quella solita vista guardando nella base di un transistore. Qui devo barare un pochino, supponendo di conoscerla. Nei circuiti reali e più complicati le impedenze da calcolare in itinere sono più semplici di quella cercata. L'impedenza di ingresso guardando nella base di un transistore vale

Infine l'impedenza vista da dove si metterà l'impedenza aggiunta  con il cortocircuito sui morsetti dove si vuole l'impedenza, figura 14d, vale evidentemente
con il cortocircuito sui morsetti dove si vuole l'impedenza, figura 14d, vale evidentemente

Con questi valori si può finalmente calcolare l'impedenza vista sull'emettitore, questa volta includendo anche la resistenza di emettitore.

Il risultato trovato in (46) non è confrontabile con gli altri trovati precedentemente, perché tutti ricavati senza  . Si potrebbe dividere numeratore e denominatore di (46) per
. Si potrebbe dividere numeratore e denominatore di (46) per  si può riconoscere il parallelo fra
si può riconoscere il parallelo fra  e
e  . Oppure si può provare a ricavare la relazione senza
. Oppure si può provare a ricavare la relazione senza  prendendo il limite per
prendendo il limite per  che tende a infinito dell'espressione (46) e si ottiene
che tende a infinito dell'espressione (46) e si ottiene

Evviva! Ancora lo stesso risultato!
Metodo di Rosenstark
Poiché le impedenze sono delle funzioni di trasferimento, qualunque metodo per il calcolo delle funzioni di trasferimento può essere più o meno convenientemente usato per calcolare una impedenza. Il metodo di Rosenstark [13] può essere applicato direttamente al calcolo delle impedenze, come mostrato il [14] e costituisce una variante della formula di Blackman. Per calcolare una impedenza à la Rosenstark, in questo caso  , si applica questa relazione
, si applica questa relazione

dove  e
e  sono l'impedenza vista dai due morsetti con un generatore pilotato azzerato (morto) e il rapporto di ritorno rispetto allo stesso generatore con i morsetti sui quali si vuole l'impedenza aperti. Questa parte è identica al calcolo secondo Blackaman. La differenza si ha che non viene usato
sono l'impedenza vista dai due morsetti con un generatore pilotato azzerato (morto) e il rapporto di ritorno rispetto allo stesso generatore con i morsetti sui quali si vuole l'impedenza aperti. Questa parte è identica al calcolo secondo Blackaman. La differenza si ha che non viene usato  ma al suo posto è presente
ma al suo posto è presente  che è l'impedenza vista dai due morsetti quando il generatore pilotato ha guadagno infinito.
che è l'impedenza vista dai due morsetti quando il generatore pilotato ha guadagno infinito.
Il vantaggio di questo metodo è di dover calcolare un solo rapporto di ritorno e due impedenze. Lo svantaggio è di dover calcolare due impedenze e un rapporto di ritorno ![]() .
.
La complessità del calcolo è circa equivalente a Blackman, anche se in qualche caso si ha che  diverge e risulta infinita. In questo caso si aggiunge una resistenza in parallelo ai morsetti dai quali si vuole calcolare l'impedenza, oppure si passa a valutare l'ammettenza con la formula
diverge e risulta infinita. In questo caso si aggiunge una resistenza in parallelo ai morsetti dai quali si vuole calcolare l'impedenza, oppure si passa a valutare l'ammettenza con la formula

in cui compaiono le ammettenze e il rapporto di ritorno  con i morsetti in cortocircuito.
con i morsetti in cortocircuito.
Nell'esempio considerato in questo articolo si può usare solo la formula (48) nei quali i valori di  e
e  sono già stati calcolati con l'analisi secondo Blackman, figure 10b e 11b ed equazioni (27) e (31).
sono già stati calcolati con l'analisi secondo Blackman, figure 10b e 11b ed equazioni (27) e (31).
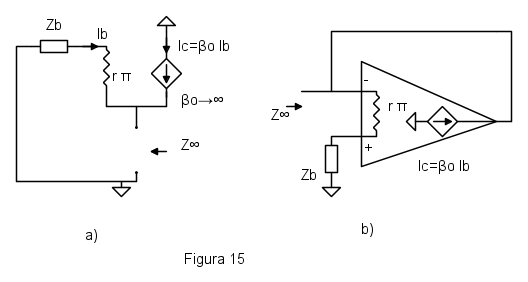
Il calcolo di  invece richiede di lavorare sul circuito di figura 15. Nella parte a) è rappresentato il circuito per il calcolo di
invece richiede di lavorare sul circuito di figura 15. Nella parte a) è rappresentato il circuito per il calcolo di  . Sembrerebbe che per calcolare questo parametro si debba già conoscere il risultato di
. Sembrerebbe che per calcolare questo parametro si debba già conoscere il risultato di  per poi prenderne il limite per
per poi prenderne il limite per
 . In realtà il caso di guadagno che tende a infinito trasforma il circuito in un nullore, in pratica in un operazionale.
. In realtà il caso di guadagno che tende a infinito trasforma il circuito in un nullore, in pratica in un operazionale.
Ridisegnando il circuito come in figura 15b si riconosce la solita configurazione di operazionale con retroazione negativa e si vede immediatamente che l'impedenza cercata è zero

perché il morsetto invertente dell'operazionale insegue la tensione del morsetto non invertente che e` a ground attraverso  .
.
Se si vuole una strada più rapida, ma più insidiosa con possibili errori, si può osservare che il circuito di figura 15a, con un generatore di corrente sull'emettitore per valutarne l'impedenza, è un sistema retroazionato con confronto in parallelo (in corrente). Quando il guadagno di anello di un sistema del genere va ad infinito, l'impedenza di ingresso viene ridotta fino a zero.
Si ha quindi, sostituendo nella (48)
 Ancora una volta lo stesso risultato.
Ancora una volta lo stesso risultato.
Uguagliando la (48) e il reciproco della (49) si ricava una importante relazione di simmetria, usata in svariate dimostrazioni

incluso ad esempio la dimostrazione della formula di Blackman (26) a partire dalla impdenza espressa come in (48).
Teorema di Scomposizione
Questo è un doppio regalo di carloc: doppio perché è lui che lo ha introdotto su EY ed è il gran sacerdote di questo metodo, essendo stato allavato a pane e Scomposizione. Il secondo regalo è che ha passato un po' di tempo a spiegarmelo, includendo i vari accorgimenti pratici per usare il teorema di Scomposizione. Una spiegazione a questo teorema si trova in [15] e [16], qui mi limeterò solo ad applicarlo.
WARNING: in questa sezione compaiono i simboli  e
e  : il primo è il guadagno di corrente del transistore bipolare, il secondo è il coefficiente di retroazione come lo si trova negli articoli del teorema, ma non ha nulla a che vedere con il transistore. In effetti quest'ultimo fattore non compare mai da solo, ma solo sempre nell'espressione
: il primo è il guadagno di corrente del transistore bipolare, il secondo è il coefficiente di retroazione come lo si trova negli articoli del teorema, ma non ha nulla a che vedere con il transistore. In effetti quest'ultimo fattore non compare mai da solo, ma solo sempre nell'espressione  .
.
L'impedenza o l'ammettenza calcolate con il teorema di scomposizione valgono (almeno in forma semplificata)


Da notare che nel teorema di scomposizione si ha per tradizione un cambiamento di segno nel sommatore di ingresso della retroazione e quindi il guadagno di anello  ha il segno negativo.
ha il segno negativo.
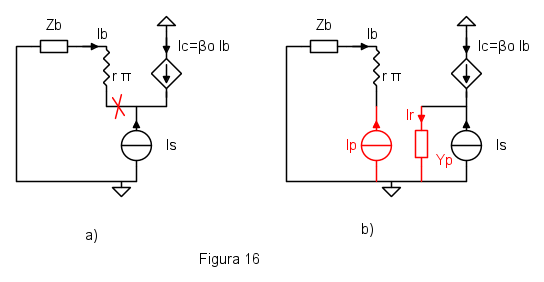
Partiamo dal circuito solito, figura 16a e mettiamo un segnale di corrente per il calcolo dell'ammettenza di emettitore.
Scegliamo la sezione di taglio dove indicato, e per far sì che il circuito non si accorga del taglio, aggiungiamo sui due lati una ammettenza  e un generatore di corrente
e un generatore di corrente  , figura 16b con la condizioni che le correnti
, figura 16b con la condizioni che le correnti  e
e  attraverso i due bipoli in rosso e le tensioni ai loro capi siano uguali.
attraverso i due bipoli in rosso e le tensioni ai loro capi siano uguali.
Con il taglio nella posizione mostrata, il parametro  è nullo, vale a dire l'ingresso
è nullo, vale a dire l'ingresso  non genera nessuna tensione ai capi del generatore
non genera nessuna tensione ai capi del generatore  : questo rende i calcoli molto più semplici.
: questo rende i calcoli molto più semplici.
Per soddisfare l'uguaglianza di tensioni e correnti fra i due bipoli rossi, è necessario che

L'ammettenza che vede il generatore di ingresso con  è data solamente data da
è data solamente data da  , non ci sono altre ammettenze in parallelo e quindi il fattore
, non ci sono altre ammettenze in parallelo e quindi il fattore  , che vuol dire che non vi sono partizioni sull'ingresso.
, che vuol dire che non vi sono partizioni sull'ingresso.
Il guadagno di anello è dato da  che in questo semplice caso vale
che in questo semplice caso vale  . A questo punto è possibile calcolare l'ammettenza vista da
. A questo punto è possibile calcolare l'ammettenza vista da  vale
vale

e quindi ancora una volta si ha lo stesso risultato.
General Feedback Theorem - GFT
Il GFT è un teorema pensato da Middlebrook nel 2001 e pubblicato nel 2005, teorema che permette di calcolare le funzioni di trasferimento di un sistema retroazionato. Se si adattano le formule del GFT al calcolo delle impedenze o alle ammettenze si ottiene


dove, come già nel metodo di Rosenstark,  o
o  è l'impedenza o l'ammettenza vista dai morsetti quando un generatore pilotato dentro l'anello di retroazione ha valore infinito.
è l'impedenza o l'ammettenza vista dai morsetti quando un generatore pilotato dentro l'anello di retroazione ha valore infinito.
I rapporti di ritorno  e
e  sono in pratica calcolati rispettivamente come
sono in pratica calcolati rispettivamente come  e
e  della formula di Blackman, cambiano solo i nomi.
della formula di Blackman, cambiano solo i nomi.
In realta` nel GFT i rapporti di ritorno  e
e  sono definiti con la doppia iniezione che annulla una uscita, ma nel caso delle impedenze il conto si semplifica notevolmente e diventa uguale a quello di Blackman (e al teorema dell'elemento aggiunto per le resistenze).
sono definiti con la doppia iniezione che annulla una uscita, ma nel caso delle impedenze il conto si semplifica notevolmente e diventa uguale a quello di Blackman (e al teorema dell'elemento aggiunto per le resistenze).
Il GFT spesso non è applicabile direttamente perché può capitare che l'impedenza o l'ammettenza vadano a zero o a infinito e le formule (56) diventano indeterminate. Si può però rimediare a questo problema aggiungendo una resistenza in più in serie a una impedenza nulla o in parallelo a una infinita e poi togliendola alla fine dei conti.
Nel circuito in esame l'impedenza vista guardando direttamente nell'emettitore e mandando il guadagno ad infinito è nulla. Mentre nel metodo di Rosenstark questo non dà problemi perché vi è un secondo addendo, nel caso del GFT l'impedenza bisogna aggiungere in serie all'emettitore una resistenza qualunque  , come mostrato in figura 17a e poi mandare a infinito il guadagno.
, come mostrato in figura 17a e poi mandare a infinito il guadagno.
Usando la tecnica del nullore, come già fatto precedentemente, e mostrata in figura 17b, si ha che l'impedenza di ingresso vale

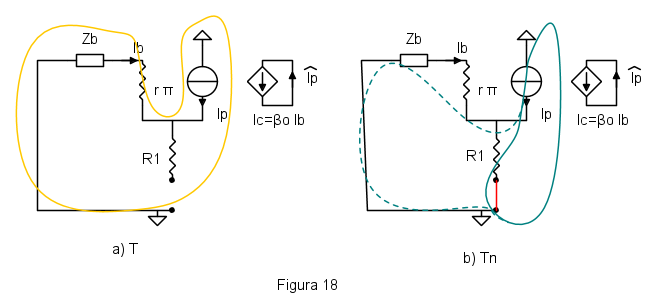
La valutazione dei rapporti di ritorno viene fatta come mostrato in figura 18, che ricalca la metodologia usata nella formula di Blackman, ma avendo aggiunto la resistenza  in serie all'emettitore.
Nella figura 18, sono indicate le maglie percorse della corrente
in serie all'emettitore.
Nella figura 18, sono indicate le maglie percorse della corrente  .
.
Il valore di  è esattamente uguale a
è esattamente uguale a  calcolato prima, e vale
calcolato prima, e vale

La valutazione di  è analoga alla precedente, ma richiede che i due morsetti siano cortocircuitati, come mostrato in figura 18b. La corrente
è analoga alla precedente, ma richiede che i due morsetti siano cortocircuitati, come mostrato in figura 18b. La corrente  si suddivide fra i due rami formati da
si suddivide fra i due rami formati da  e
e  e la corrente di base, che poi eccita il generatore pilotato e fa scorrere
e la corrente di base, che poi eccita il generatore pilotato e fa scorrere  vale
vale

e quindi la corrente del generatore pilotato vale  e quindi il rapporto di ritorno
e quindi il rapporto di ritorno  vale
vale

Sostituendo in (56a) i valori trovari in (57), (58) e (59) si ottiene l'impedenza  vista guardando nell'emettitore ma includendo anche la resistenza
vista guardando nell'emettitore ma includendo anche la resistenza 

In questo risultato si riconosce la solita impedenza  vista guardando dentro l'emettitore in serie a
vista guardando dentro l'emettitore in serie a  che era stata aggiunta preliminarmente per evitare forme indeterminate.
che era stata aggiunta preliminarmente per evitare forme indeterminate.
Legame con altri metodi
I vari metodi "moderni" di analisi delle reti, di cui il GFT fa parte, non sono scorrelati fra di loro, ma si può mostrare che sono fra di loro equivalenti: solo la convenienza di calcolo o di familiarità porta a utilizzarne uno piuttosto che un altro. Ad esempio il GFT e la formula di Blackman sono strettamente correlati attraverso il metodo di Rosenstark.
Riscriviamo il GFT usando al posto di  e
e  rispettivamente i simboli
rispettivamente i simboli  e
e  . I due metodi usano simboli diversi per ragioni storiche, ma indicano la stessa quanità.
. I due metodi usano simboli diversi per ragioni storiche, ma indicano la stessa quanità.
Queste ragioni storiche sono dovute al fatto che Blackman è nato per il calcolo delle impedenze e non si è mai evoluto nel calcolo delle funzioni di trasferimento. Invece il GFT è stato trovato per calcolare le funzioni di trasferimento, usando la tecnica di doppia iniezione, ma non è mai stato usato per le impedenze: essendosi sviluppati in contesti diversi hanno fatto uso di notazioni differenti.
L'impedenza secondo il GFT scritta con la notazione di Blackman diventa

e usando la (52) che permette di ricavare

sostituendo in (62) si ha

che è appunto la formula di Blackman. Anche il teorema dell'elemento aggiunto usato per il calcolo delle impedenze è equivalente al GFT e a tutti gli altri metodi. Una delle formula generale per questo metodo dice che

dove  è l'impedenza vista dai morsetti dove si vuole trovare l'impedenza quando
è l'impedenza vista dai morsetti dove si vuole trovare l'impedenza quando  ovvero non c'e` l'impedenza che si vorrà aggiungere in seguito in parallelo al circuito.
ovvero non c'e` l'impedenza che si vorrà aggiungere in seguito in parallelo al circuito.
Con le notazioni usate in precedenza si potrebbe rinominare  perché è l'impedenza vista quando un parametro, in questo caso
perché è l'impedenza vista quando un parametro, in questo caso  va ad infinito. In quasi tutti i casi precedenti si è lavorato mandando a zero o a infinito il guadagno di un generatore pilotato, ma la stessa cosa può essere fatta su qualunque parametro della rete, incluso il valore di un componente.
va ad infinito. In quasi tutti i casi precedenti si è lavorato mandando a zero o a infinito il guadagno di un generatore pilotato, ma la stessa cosa può essere fatta su qualunque parametro della rete, incluso il valore di un componente.
Il rapporto di impedenze  e
e  sono in realta` dei rapporti di ritorno di un partitore di impedenze, in cui uno dei due elementi è l'impedenza aggiunta e l'altro è l'impedenza che si vede guardando dentro la rete ai morsetti dove si collegherà l'elemento aggiunto.
sono in realta` dei rapporti di ritorno di un partitore di impedenze, in cui uno dei due elementi è l'impedenza aggiunta e l'altro è l'impedenza che si vede guardando dentro la rete ai morsetti dove si collegherà l'elemento aggiunto.
Il fatto che un semplice partitore di due impedenze sia un sistema retroazionato, con tanto di rapporto di ritorno o guadagno di anello, non è molto noto, ma è illustrato in [21]. I due rapporti di impedenze sono quindi il (reciproco) del rapporto di ritorno valutato fra l'impedenza aggiunta e l'impedenza vista nella rete quando i morsetti dove si vuole trovare l'impedenza sono in cortocircuito o in circuito aperto, e quindi i due rapporti di ritorno sono appunto  e
e  , mostrando che anche il teorema dell'elemento aggiunto per le impedenze è equivalente al GFT.
, mostrando che anche il teorema dell'elemento aggiunto per le impedenze è equivalente al GFT.
E Miller?
E il teorema di Miller può essere usato per calcolare l'impedenza di emettitore? Prima della risposta alcune curiosità su questo teorema.
Miller non ha "inventato" il suo teorema, ha solo riportato in un articolo [19] un effetto di abbassamento dell'impedenza di ingresso che si verificava nei tubi elettronici. L'effetto Miller ha cominciato ad essere generalizzato e chiamato teorema molto dopo la sua pubblicazione nel 1920, probabilmente nei libri di Millman Halkias intorno al 1967.
L'evoluzione del teorema di Miller ha generato in totale 4 diverse versioni, a seconda del tipo di retroazione coinvolta [20]. Neanche considerando queste estensioni non sono riuscito a trovare un modo per utilizzarlo nel calcolo dell'impedenza di emettitore ![]()
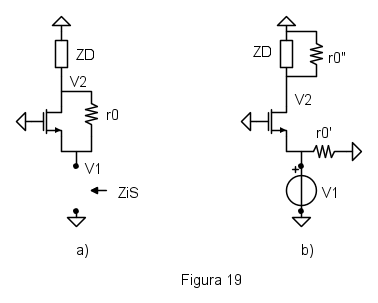
D'altra parte però il teorema di Miller "standard" è importante nei problemi per il calcolo dell'impedenza di ingresso e pare brutto non mostrarne un esempio. Per questa ragione in questa sezione si userà il teorema di Miller per valutare in modo approssimato l'impedenza vista nel source di un MOS quando è presente l'effetto di modulazione della lunghezza di canale (impropriamente detto nel MOS effetto Early) e una resistenza di carico sul drain. Il circuito di riferimento è in figura 15a, dove si considera un MOS ideale e si mette in evidenza, disegnandola fuori dal dispositivo, la sua resistenza  . Il mos che rimane, dopo aver estratto la resistenza
. Il mos che rimane, dopo aver estratto la resistenza  è quindi un dispositivo ideale e la resistenza vista guardando nel source di un mos ideale vale
è quindi un dispositivo ideale e la resistenza vista guardando nel source di un mos ideale vale 
In questo circuito si ha una retroazione parallelo/parallelo intorno allo stadio con guadagno, e si è nelle condizioni di applicare facilmente il teorema di Miller "solito" che richiede di conoscere l'amplificazione  . Supponendo di sapere questa amplificazione
. Supponendo di sapere questa amplificazione  , si può suddividere la resistenza
, si può suddividere la resistenza  , connessa fra uscita e ingresso, in due resistenze
, connessa fra uscita e ingresso, in due resistenze  ed
ed  connesse fra i due nodi ai quali era collegata l'originale
connesse fra i due nodi ai quali era collegata l'originale  e ground, come mostrato in figura 15b.
e ground, come mostrato in figura 15b.
Il valore delle due resistenze sdoppiate con Miller è


mentre l'amplificazione  dello stadio a gate comune vale
dello stadio a gate comune vale

E di qua si vede la difficoltà di usare il teorema di Miller senza approssimazioni: l'amplificazione dipende da  la quale a sua volta dipende da
la quale a sua volta dipende da  . Si può risolvere in modo esatto l'equazione derivante dal mettere insieme (66b) e (67), ma non si guadagnerebbe tempo rispetto ad altri metodi.
. Si può risolvere in modo esatto l'equazione derivante dal mettere insieme (66b) e (67), ma non si guadagnerebbe tempo rispetto ad altri metodi.
Una approssimazione che rende il teorema di Miller comodo da usare consiste nel supporre  , in questo modo la (66b) fornisce
, in questo modo la (66b) fornisce  e l'amplificazione può essere calcolata facilmente. Ovviamente quando si introduce una ipotesi, qui l'amplificazione molto maggiore di 1, si deve poi verificare che sia corretta.
e l'amplificazione può essere calcolata facilmente. Ovviamente quando si introduce una ipotesi, qui l'amplificazione molto maggiore di 1, si deve poi verificare che sia corretta.
Altra possibile approssimazione che si può usare per applicare il teorema di Miller si ha quando  : in questo caso si può completamente trascurare l'effetto di
: in questo caso si può completamente trascurare l'effetto di  nel calcolo del guadagno. In pratica usando queste due diverse approssimazioni, e supponendo il guadagno elevato o la resistenza
nel calcolo del guadagno. In pratica usando queste due diverse approssimazioni, e supponendo il guadagno elevato o la resistenza  per l'amplificazione si ottengono le seguenti espressioni
per l'amplificazione si ottengono le seguenti espressioni


Supponendo di poter usare l'approssimazione (68b) si ottiene per 

In questo circuito l'amplficazione è positiva e quindi la resistenza  è negativa: in effetti in questo circuito la retroazione è positiva, e in generale una resistenza negativa potrebbe dare fenomeni di instabilità.
è negativa: in effetti in questo circuito la retroazione è positiva, e in generale una resistenza negativa potrebbe dare fenomeni di instabilità.
L'impedenza di ingresso  , includendo l'effetto della modulazione di lunghezza di canale è data dal parallelo fra
, includendo l'effetto della modulazione di lunghezza di canale è data dal parallelo fra  e l'impedenza di ingresso del source in un mos ideale, che come detto prima è
e l'impedenza di ingresso del source in un mos ideale, che come detto prima è  . Si ha quindi
. Si ha quindi

Si può verificare, ma non viene fatto qui, che l'impedenza complessiva di ingresso è sempre positiva, e quindi il circuito è stabile.
Conclusioni
A forza di fare sono riuscito a finire questa carrellata descrittiva su metodi vari per calcolare l'impedenza fra due morsetti. Non ho messo dimostrazioni e non ho neanche approfondito quando invece sarebbe forse stato il caso, ad esempio con i generatori di prova, mostrando praticamente come usare la sovrapposizione degli effetti. Queste tecniche sono ben spiegate in [22].
Un bravo progettista ovviamente non deve sapere tutta questa roba, ma più cose si sanno meglio è. Tutti questi metodi sono degli attrezzi che il progettista mette nella sua valigetta degli attrezzi, la sua tool-box, pronti ad essere usati quando necessario. Probabilmente si può fare tutto con pochi metodi, ma si rischia di non avere lo strumento giusto a disposizione. In fondo quando si porta la macchina dal meccanico, si spera che abbia tutti gli strumenti necessari per lavorare su qualsiasi guasto, non che abbia solo il martello con cui fare tutto!
Ringraziamenti
Un ringraziamento a dirtydeeds per i suggerimenti sull'uso di Latex, e a carloc per le chiacchierate sui teoremi strani che fanno a Pisa!
pietrobaima e brunovalente si sono gentilmente prestati a rileggere le bozze cercando errori e strafalcioni vari.
Bibliografia e Sitografia
[1] Gray, Meyer, Hurst, and Lewis, Analysis and Design of Analog Integrated Circuits, Wiley, 5th ed. 2009
[2] R.D. Middlebrook, Low Entropy Expressions, Design Oriented Analysis Slides, Ch. 2, 2007.
[3] R.D. Middlebrook, Low entropy expressions, Conf. on New Approaches to Undegraduate Educations, Santa Barbara 1992.
[4] G. Weiss, Network Theorems for Transistor Circuits, IEEE Trans. on Ed. Vol 37. No. 1, Feb 1994, pp 36-41
[5] R. Kelly, Electronic Circuit Analysis and Design by Driving-Point Impedance Techniques, IEEE Trans. on Ed. Vol 13 No. 3, Sept 1970, pp. 154-167
[6] T.A. Howard, Circuit Analysis Using the Driving-Point-Impedance Technique, Sandia Laboratories Report No. SC-M-71 0896, Feb. 1972
[7] R.B. Blackman, Effect of Feedback on Impedance, BSTJ Vol 22 No. 3, Oct. 1943, pp. 269-277
[8] A. Abramovitz, Several Alternative Derivations of Blackman's Impedance Relation, J. of Circuits, Systems, and Computers Vol 18 No. 5, Aug. 2009, pp 909-921
[9] R.D. Middlebrook, The Input/Output Impedance Theorem, Design Oriented Analysis Slides, Ch. 7, 2007.
[10] C. Beccari, Teoria dei Circuiti Elettronici, CLUT 1996
[11] R.D. Middlebrook, Null double injection and the extra element theorem, IEEE Trans. on Ed., Vol. 32 No 3, Aug. 1989, pp 167-180
[12] V. Vorperian, Fast Analytical Techniques for Electrical and Electronic Circuits, Cambridge University Press, June 2002
[13a] S. Rosenstark, Feedback Amplifier Principles, McMillan Publ. Co., 1986
[13b] S. Rosenstark, A Simplified Method of Feedback Amplifier Analysis, IEEE Trans. on Ed.. Vol. 17 No 4, Nov. 1974, pp 192-198
[14] D'Amico et alii, Resistance of Feedback Amplifiers: A Novel Representation, IEEE Trans. on Circ. & Syst. II, Vol. 54 No 4, Apr. 2007, pp 297-302.
[15] Carloc, Teorema di Scomposizione, EY Giu 2012
[16] B. Pellegrini, Improved Feedback Theory, IEEE Trans. on Circ. and Syst. I, Vol.56 No 9, Sept. 2009, pp 1949-1959
[17] R.D. Middlebrook, Null Double Injection and General Feedback Theorem,Design Oriented Analysis Slides, Ch. 11, 2007
[18] R.D. Middlebrook, The General Feedback Theorem: A Final Solution for Feedback Systems, IEEE Microwave Magazine, Vol. 7 No 2, Apr 2006, pp 50-66
[19] J.M. Miller, Dependence of the input impedance of a three-electrode vacuum tube upon the load in the plate circuit, Scientific Papers of the Bureau of Standards, Vol. 15, 1920, pp. 367-385
[20] Miron, Ogrutan, and Wardegger, Two new Miller theorems, IEE Proc., Vol. 133, Pt G, No 5, Oct 1986, pp. 271-272.
[21] IsidoroKZ, La controreazione nascosta, EY Lug. 2010
[22] D.L. Skaar, W.L. Brown, Emphasizing Some Little-Used Theorems in Introductory Network Analysis, IEEE Trans. on Ed., Vol. 39 No 4, Nov 1996, pp 352-539

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)