ElectroYou - la comunità dei professionisti del mondo elettrico

Vai a: navigazione, ricerca

Questi articoli nascono da alcune richieste che periodicamente si riaffacciano, specie nel periodo natalizio, richieste miranti a sapere come montare lunghe stringhe di led e alimentarle direttamente da rete. Poiche' si dice che l'assassino torni sempre sul luogo del delitto, dopo gli articoli sulle stringhe di led [1] e sugli alimentatori transformerless [2], torno a riprendere questi argomenti.

Ho sentito domandare "se metto 63 led da 3.5V in serie, posso collegarli direttamente alla 220? In fondo 63x3.5=220.5". Per evitare danni (probabili) a cose e persone, meglio chiarire le idee, e invitare a non fare di questi circuiti!

Alimentare un circuito direttamente da rete, senza un trasformatore in mezzo, e` quasi sempre una pessima idea. Innanzi tutto il circuito NON E` ISOLATO!, il che vuol dire che toccando i conduttori si prende la scossa! Se poi le lunghe stringhe di led sono addobbi natalizi messi all'aperto, oppure in casa ci sono animali che giocano con i fili e li mordono o rosicchiano, il pericolo e` clear and present!

La seconda ragione per cui un circuito del genere potrebbe essere sconsigliabile e` che in caso di guasto la corrente disponibile da una connessione diretta alla rete potrebbe essere molto elevata creando un concreto rischio di incendio.

Infine una connessione diretta alla rete deve poter sopportare tutte le extratensioni che si possono avere sulla rete stessa, in particolare i voltage sourge. Gli alimentatori ben fatti, oltre all'isolamento, hanno anche tutte le protezioni che riguardano questi ultimi due punti. Un alimentatore diretto da rete di solito viene visto nell'ottica del "cosi` risparmio" e si tende a non mettere le protezioni, ad esempio fusibili, transzorb... Uomo avvisato...

In questi due articoli saranno analizzati, valutando pro e contro, alcuni circuiti adatti ad alimentare lunghe stringhe di led che richiedono tensioni di un centinaio di volt o piu`, con correnti medie dell'ordine delle decine di milliampere, con collegamente a una rete a $50\,\text{Hz}$ e $230\,\text{V}$ . Led che richiedono correnti piu` elevate, ad esempio da un centinaio di milliampere a salire, dovrebbero essere alimentati con appositi alimentatori elettronici a corrente costante.

In questo articolo sara` dapprima analizzato il modello della rete e dei led in serie, passando poi all'analisi e progetto di un circuito a caduta fatta con una resistenza che alimenta i led con corrente pulsante.

Nell'articolo successivo [9] saranno invece analizzati i circuiti a caduta resistiva e alimentazione a corrente costante, per poi passare ai corrispondenti circuiti con caduta a condensatore e corrente dei led sia costante che pulsante.

Dato che i led richiedono corrente unidirezionale, si usera` un raddrizzatore a ponte per raddrizzare la tensione alternata di rete.

Pare inoltre definitivamente appurato che non sia in grado di tenere le cose semplici. In questi articoli ci sono parecchie formule, e dietro ci sono tanti conti che ho dovuto fare per ricavarle, che per decenza non riporto. Avevo pensato a una appendice, ma come regalo di Natale non la scrivero`.

Considerato pero` che questi sono circuiti potenzialmente pericolosi, i conti in fase di progetto si devono fare tutti!. Dice il saggio che l'elettronica non e` semplice, se si vuole capire davvero come funziona.

Indice

1 Rete e LED: modelli
- 1.1 Tensione di rete
- 1.2 LED
2 Regolazione a resistenza - Corrente pulsante
3 Continua... alla prossima puntata!
4 Bibliografia

Rete e LED: modelli

Per fare due conti sensati e` necessario sapere come e` fatta la tensione di rete e come si comportano i led. Prima di cominciare ad analizzare i vari circuiti vediamo come sono fatti la tensione di rete e i led:

Tensione di rete

La tensione di rete dovrebbe essere di valore efficace di $230\,\text{V}$ , sinusoidale, frequenza $50\,\text{Hz}$ . Mentre la frequenza e` decisamente molto precisa, il valore di tensione puo` variare di un $10\%$ , a seconda della posizione geografica dell'utente, dell'ora del giorno... E anche la forma sinusoidale puo` lasciare abbastanza a desiderare.

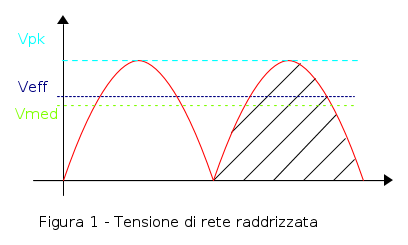
La tensione di rete raddrizzata da un ponte e` mostrata in figura 1, dove sono evidenziati i tre valori importanti di questa forma d'onda: il valore efficace o valore rms $V_\text{eff}\,$ , il valore di picco $V_\text{pk}\,$ e il valore medio $V_\text{med}\,$ della forma d'onda raddrizzata.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Per la rete domestica il valore di $230\,\text{V}$ si riferisce al valore efficace. Il valore di picco e` maggiore, ed e` di $325\,\text{V}$ mentre quello medio e` nullo. Dopo aver raddrizzato la tensione di rete, la tensione di picco e quella efficace rimangono praticamente inalterate, mentre il valore medio, in pratica l'altezza a cui arriva l'area di un semiperiodo spalmata uniformemente su un semiperiodo, diventa di $207\,\text{V}$ .

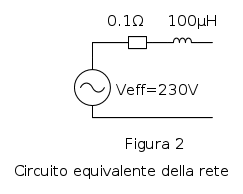
L'impedenza della rete in questo caso dovrebbe essere poco importante, si spera di non avere dei corticircuiti franchi, ma visto che usero` il simulatore non costa nulla mettere due valori di resistenza e induttanza di sorgente. Il circuito equivalente della rete che sara` utilizzato e` il seguente:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Da notare che in caso di cortocircuito franco, la corrente efficace calcolata con questo modello supera i $2\,\text{kA}$ , ed e` un valore abbastanza reale: occhio ai corticircuiti!

Da queste prime considerazioni dovrebbe essere evidente perche' non e` possibile collegare con un raddrizzatore 63 led in serie direttamente alla rete: la tensione di rete e` continuamente variabile, fra $0\,\text{V}$ e $325\,\text{V}$ .

Sulla tensione di rete, che in realta` e` una sinusoide un po' ammaccata, possono essere sovrapposti dei brevi impulsi di sovratensione, chiamati surge, che possono danneggiare i led o l'isolamento del circuito. Gli impulsi piu` energetici che si possono trovare hanno l'ampiezza di alcuni kilovolt (si`, proprio migliaia di volt!) e durata di qualche decina di microsecondi, e solitamente sono generati da temporali.

LED

Il LED e` un diodo il cui uso e proprieta` sono descritti in molti posti, alcuni articoli sono riportati in bibliografia [1][3][4][5]. In particolare [5] mostra molto chiaramente il comportamento non lineare del LED e [4] permette di calcolare il modello SPICE di un LED non presente in libreria.

In questo articolo, nei calcoli preliminari, non e` necessario arrivare questi livelli di dettaglio e il modello per tanti led collegati in serie sara` semplicemente un modello lineare valido intorno alla corrente media di funzionamento del led, o meglio della stringa di led: in pratica i led in conduzione saranno modellati da una resistenza in serie a una batteria, come mostrato in figura 3B:

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Se sono a disposizione le curve caratteristiche dei LED utilizzati e` possibile ricavare la tensione alla corrente nominale e la pendenza della caratteristica tensione/corrente intorno al valore della corrente nominale. Altrimenti se si conosce solo la tensione tipica del led alla corrente tipica (ad esempio $V_\text{led}=3.6\,\text{V}$ alla corrente $I_\text{led}=20\,\text{mA}$ ), si puo` assumere, per LED piccoli una resistenza interna di una decina di ohm.

Se il led viene usato con ampie escursioni di corrente, come nei circuiti a corrente pulsante, in cui la corrente istantanea va da corrente nulla al doppio o al triplo della corrente media, la resistenza serie del modello del led e` meglio sia un po' piu` piccola di una decina di ohm per led, ad esempio si possono considerare pochi ohm per ogni led di quelli normali da $20\,\text{mA}$ .

A questo punto per alimentazioni in continua si fa questo semplice calcolo: una corrente di $20\,\text{mA}$ (dato del diodo) attraverso una resistenza da $10\,\Omega$ (valore scelto a buon senso) da` una caduta di tensione di $200\,\text{mV}$ . Visto che vogliamo sul LED $3.6\,\text{V}$ a $20\,\text{mA}$ , e $200\,\text{mV}$ li fa di caduta la resistenza, attribuiamo al LED una tensione di soglia di $V_\text{s}=3.4\,\text{V}$

Se invece si fosse usato lo stesso led in un circuito a corrente pulsante, ma con valore medio sempre di $20\,\text{mA}$ , si puo` prendere una resistenza minore, ad esempio $5\,\Omega$ , e si ha una tensione di soglia di $V_\text{s}=3.5\,\text{V}$ .

La formula generale per trovare la tensione di soglia e` questa (da usarsi se non si hanno dati migliori):

$(1)\qquad V_\text{s}=V_\text{led}-R_\text{int}I_\text{led}\,$

Nella formula la resistenza interna $R_\text{int}\,$ , per diodi da qualche decina di milliampere, e` dalle parti di $3-10\,\Omega$ circa (mi sembra di averlo gia` detto :) ).

Quando si mettono in serie tanti led, basta sommare tutte le resistenze di tutti i led e sommare tutte le tensioni di soglia per trovare la resistenza interna complessiva e la tensione di soglia complessiva. Da notare che si possono anche mttere in serie LED di tipo diverso, basta che funzionino tutti alla stessa corrente.

Se si vogliono mettere in serie ad esempio 40 led bianchi con le caratteristiche indicate prima, e cerhiamo un modello per alimentazione in corrente continua, avremo una resistenza complessiva di $10\,\Omega\times 40=400\,\Omega$ e una tensione di soglia complessiva di $3.4\,\text{V}\times 40=136\,\text{V}$

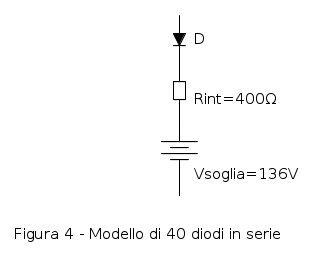
Il circuito equivalente e` quello in figura 4, a cui si e` aggiunto un diodo per ricordare (e ricordarci) che i LED conducono in un verso solo. In questo modo il nostro modello "primitivo" puo` anche essere usato dentro SPICE, e la caduta sul diodo e` assolutamente trascurabile.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Quando nel modello scorre la corrente di $20\,\text{mA}$ , la caduta complessiva e` di circa $3.6\,\text{V}\times 40=144\,\text{V}$

Da notare che questo e` un modello approssimato del led, il risultato nel circuito puo` essere diverso dal calcolato anche di un 10%, sia per le approssimazioni del modello (linearizzazione), sia per i valori nominali assunti rispetto a quelli reali dei led utilizzati.

La luce emessa da un led e` proporzionale alla corrente MEDIA che scorre nel led. In caso di alimentazione in continua, questa e` la corrente media. In caso di alimentazione a corrente pulsante, la luce dipende dalla corrente media che scorre nel led: in realta` la luce emessa pulsa come la corrente, ma l'occhio fa la media della luce vista.

Regolazione a resistenza - Corrente pulsante

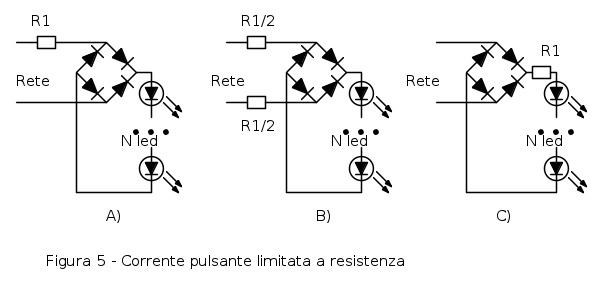
Lo schema piu` semplice per alimentare con una corrente media ragionevolmente regolata una stringa di led consiste nell'usare il circuito A) o meglio ancora il B) di figura 5, in cui la resistenza di limitazione $R_1\,$ e` stata suddivisa in due resistenze di valore dimezzato. Il circuito C), pur sembrando assolutamente identico dal punto di vista elettrico, non deve essere usato.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

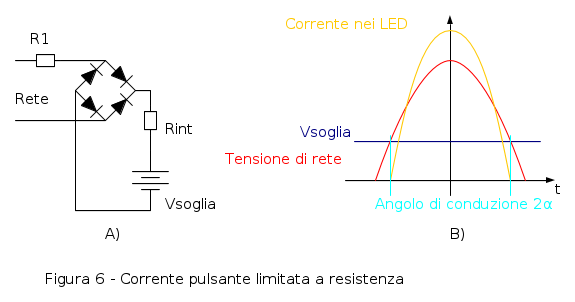
Il funzionamento di questo circuito e` semplice, se si immagina la serie dei diodi led sostituita dal suo circuito equivalente, come in figura 6A. Finche' la tensione di rete e` al di sotto della tensione di soglia, data dalla somma della soglia di tutti i diodi, non circola corrente e i diodi sono spenti.

Quando la tensione di rete arriva alla tensione di soglia, comincia a scorrere una corrente che e` data dalla differenza di tensione di rete meno la tensione di ingresso, divisa per la somma delle resistenze. In figura 6B sono rappresentate le varie tensioni e in giallo la corrente attraverso i led.

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

In pratica la resistenza piu` importante e` $R_1\,$ , e se si vuole essere pignoli si puo` anche aggiungere la resistenza interna dei led $R int$ ottenendo per la corrente, quando $V_\text{rete}>V_\text{s}\,$ ,

$(2)\qquad I_\text{led}=\frac{V_\text{rete}-V_\text{s}}{R_1+R_\text{int}}$

Il periodo lungo il quale scorre corrente nei diodi si chiama tempo di conduzione, che puo` anche essere visto come un angolo, dato che si parla di funzioni sinusoidali. Dall'inizio della conduzione alla fine della conduzione l'angolo, che si indica con $2\alpha_c\,$ vale

$(3)\qquad 2\alpha_c = 2 \arccos \left ( \frac{V_\text{s}}{V_\text{pk}} \right )$

Conviene, almeno per me nel fare i conti, definire il rapporto fra tensione di soglia e tensione di picco e chiamarlo ad esempio $k_s=\frac{V_\text{s}}{V_\text{pk}}$ . Questo semplifica un po' le espressioni e di parecchio i conti.

La corrente media che scorre attraverso i led, e che dipende dal valore di $R_1\,$ e` calcolata spalmando uniformemente la forma d'onda gialla su un semiperiodo e calcolando quanto viene lo spessore della spalmatura.

Il valore della resistenza $R_1\,$ per ottenere la corrente $I_\text{led}\,$ voluta e`

$(4)\qquad \begin{align} R_1&=\frac{2}{\pi I_\text{led}}\left (\sqrt{V_\text{pk}^2-V_\text{s}^2}-2V_\text{s}\arccos \left( \frac{V_\text{s}}{V_\text{pk}}\right ) \right )-R_\text{int}=\\ &=\frac{2V_\text{pk}}{\pi I_\text{led}}(\sqrt{1-k_s^2}-k_s\arccos(k_s))-R_\text{int} \end{align}$

(spiacente per la formula complicata, la si potrebbe approssimare, ma al giorno d'oggi le calcolatrici scientifiche si trovano ovunque, quindi la formula completa puo` starci. Bisogna solo fare attenzione e calcolare l'arcocoseno con la calcolatrice in radianti)

La corrente e` impulsiva, a 100Hz, il doppio della frequenza di rete. La corrente parte da 0 e sale fino a un valore di picco pari a

$(5)\qquad I_\text{pk}=\frac{V_\text{pk}-V_\text{s}}{R_1+R_\text{int}}=\frac{V_\text{pk}(1-k_s)}{R_1+R_\text{int}}=\frac{\pi}{2}\frac{1-k_s}{\sqrt{1-k_s^2}-k\arccos(k_s)}I_\text{led}$

Questo valore puo` essere significativamente piu` alto della corrente media. Purtroppo queste espressioni diventano difficili da scrivere e da interpretare, conviene fare un grafico in funzione di $k_s\,$ , ricordando che tipicamente si sta su $k_s<0.4-0.5\,$ . Il rapporto fra corrente di picco e corrente media e` in figura 7.

Per tensioni di soglia molto piu` basse della tensione di picco di rete, il rapporto e` circa 1.6. Con tensione di soglia dei led del $40\%\,$ della tensione di rete ( $k_s=0.4\,$ ), cioe` $130\,\text{V}$ , la corrente di picco e` di circa 2.1 volte la corrente media. Al $70\%\,$ il rapporto e` di 3 volte ma non conviene andare a lavorare con tensioni di stringa cosi` alta sia per lo stress di corrente che per altre ragioni che saranno discusse in seguito.

Figura 7 - Rapporto corrente di picco/corrente media

Una buona approssimazione del valore della corrente di picco quando $k_s\le 0.5\,$ e`

$(6)\qquad I_\text{pk}=I_\text{led}(1.57+1.45k_s)\,$

La corrente impulsiva che circola nei led e in $R_1\,$ ha un valore efficace abbastanza macchinoso da calcolare, anche qui un grafico da` una visione rapida dell'andamento della corrente efficace in funzione di $k_s\,$ e della corrente media nel led.

Figura 8 - Rapporto corrente di efficace/corrente media

Anche qui una approssimazione lineare da` una buona stima della corrente efficace quando $k_s\le 0.5\,$ :

$(7)\qquad I_\text{rms}=I_\text{led}(1.11+0.48k_s)\,$

La potenza dissipata dalla resistenza $R_1\,$ , che ha una espressione molto complicata, ha il buon gusto di avere una espressione approssimata molto semplice:

$(8)\qquad P_{R_1}=V_\text{pk}I_\text{led}\frac{\pi}{4}(1-k_s)$

Questa espressione e` una sovrastima dell'effettiva potenza dissipata poiche e` stata calcolata includendo in $R_1\,$ anche la potenza dissipata dalla resistenza interna $R_\text{int}\,$ , e poi e` stata fatta l'approssimazione lineare.

E con questa ci sono tutte le formule che servono per progettare questo circuito.

Rimangono due parametri da considerare: l'efficienza e la sensibilita` della corrente media al variare della tensione di picco.

Con i soliti lunghi e noiosi calcoli si ottiene una efficienza in funzione di $k_s\,$ mostrata nel grafico di figura 9. L'efficienza e` stata calcolata come rapporto fra potenza che va ai led diviso per la potenza di ingresso, includendo nelle perdite anche la potenza dissipata su $R_\text{int}\,$ (che, ricordiamo, e` solo un pezzo di un modello).

Figura 9 - Efficienza

Si vede che l'efficienza e` praticamente uguale al fattore $k_s\,$ . In realta` nell'intervallo $0.3<k_s<0.55\,$ l'efficienza e` almeno del $5\%\,$ maggiore dell'approssimazione lineare.

Infine la sensibilita` alle variazioni della tensione di picco e` un parametro importante perche' indica di quanto cambia la corrente media nei led, e quindi la luce emessa, al variare della tensione di rete.

Il calcolo della sensibilita` relativa [6] da` questo sconfortante risultato

$(9)\qquad S^{I_\text{led}}_{V_\text{pk}}=\frac{\sqrt{1-k_s^2}}{\sqrt{1-k_s^2}-k_s\arccos(k_s)}$

Il risultato e` sconfortante perche' mostra una rapida crescita per elevati valori di $k_s\,$ , come si vede dalla successiva figura 10:

Figura 10 - Sensibilita` di Iled al variare di Vpk

gia` con $k_s=0.5\,$ si ha una sensitivity di $2.6\,$ , il che significa che una variazione del $10\%\,$ della tensione di rete provoca una variazione del $26\%\,$ della corrente media, con ampi cambi di luminosita` e possibile overstress dei led.

Per questa ragione e` opportuno rimanere con stringhe di lunghezza limitata, in modo che la tensione non superi il $40\%-50\%\,$ circa della tensione di picco della rete, in pratica si possono alimentare stringhe fino a circa $130\text{V}-160\text{V}\,$ .

Esempio di progetto

Proviamo qui a sviluppare il calcolo per alimentare una stringa di 40 led bianchi, di tipo NSPW500BS [7] prodotto da Nichia. I dati nominali sono $V_F=3.6\,\text{V}$ a $I_\text{led}=20\,\text{mA}$ . Essendo un diodo a bassa corrente utilizzato pero` con correnti massime abbastanza maggiori di quella media, si puo` ipotizzare una resistenza interna di $5\,\Omega$ e quindi la tensione di soglia del singolo led vale (equazione (1)) $V_\text{s}=3.6\text{V}-5\Omega\times 20\text{mA}=3.5\text{V}$ .

Essendoci 40 led in serie si ha che la tensione di soglia totale e` di $V_\text{s}=140\,\text{V}$ e la resistenza interna complessiva e` di $R_\text{int}=200\,\Omega$ .

La prima cosa da calcolare e` $k_s=\frac{V_\text{s}}{V_\text{pk}}=\frac{140\text{V}}{325\text{V}}=0.4308$ . Volendo una corrente media di $I_\text{led}=20\,\text{mA}$ si ricava dall'equazione (4) il valore di $R_1\,$ :

$(10)\quad \begin{align} R_1&=\frac{2V_\text{pk}}{\pi I_\text{led}}(\sqrt{1-k_s^2}-k_s\arccos(k_s))-R_\text{int}=\\ &=\frac{2\times 325 \text{V}}{\pi \times 20\text{mA}}(\sqrt{1-0.4308^2}-0.4308\arccos(0.4308))-200\Omega=\\ &=4120\,\Omega \end{align}$

Come in tutte le formule di questi post, l'arco coseno deve essere calcolato con la calcolatrice in radianti, non in gradi.

Se si usano due resistenze di valore dimezzato, una per ogni ramo della rete, come in figura 5B), il valore di ciascuna resistenza e` la meta` di quanto calcolato sopra per $R_1\,$ intera.

La corrente di picco nei led, calcolato con l'equazione approssimata (6) oppure dalla figura 7, vale

$(11)\qquad I_\text{pk}=20\text{mA}(1.57+1.45\times.4308)=44\,\text{mA}$

circa, mentre la corrente efficace che circola nella maglia vale, sempre usando l'espressione approssimata (7), circa

$(12)\qquad I_\text{rms}=20\text{mA}(1.11+0.48\times.4308)=26\,\text{mA}$

La potenza dissipata dalla resistenza $R_1\,$ e` data da (8)

$(13)\qquad P_{R_1}=325\text{V}\times 20\text{mA}\times.785(1-.4305)=2.9\,\text{W}$ .

Se si usano due resistenze di valore dimezzato, una per ogni ramo della rete, come in figura 5B), la dissipazione di ciascuna resistenza e` la meta` di quanto calcolato per $R_1\,$ intera.

L'efficienza del circuito e` praticamente uguale a $k_s\,$ , circa il $5\%\,$ maggiore, cioe` si va dalle parti del $48\%\,$ , e la sensitivity (equazione (9) o figura 10) e` di $2.2\,$ : una variazione del $10\%\,$ nella tensione di rete fa cambiare la corrente dei led di poco piu` del $20\%\,$ .

Simulazione

Dato che LTspice ha nella libreria di base il led usato in questo esempio, si puo` utilizzare il simulatore per vedere che cosa capita nella "realta` virtuale" del simulatore.

Lo schema simulato e` nella figura 11:

Figura 11 - Circuito simulato

insieme con la versione in cui il carico e` effettivamente formato da 40 diodi led. La corrente che circola nel carico e` mostrato nella figura seguente

Figura 12 - Correnti nel carico, modello lineare e led

La curva rossa e` la corrente attraverso i led di LTSpice, mentre quella verde e` la curva attraverso il modello lineare. I valori nei due casi, come calcolati con il simulatore, sono i seguenti:

TABELLA 1
Parametro	Calcolo	Modello lineare	LED di LTSpice
I media	20mA	19.8mA	21.6mA
I picco	44mA	42.4mA	43.8mA
I rms	26mA	25.8mA	27.3mA
Pot su R1	2.9W	2.8W	3.1W
Efficienza	48%	49%	49%
Sensitivity	22%	21.7%	19.4%

La sensitivity e` stata calcolata aumentando la tensione di rete del $10\%\,$ e calcolando il corrispondente aumento percentuale della corrente media.

La differenza fra modello lineare e circuito con i 40 led in serie e` dovuto alla tensione di led data dal modello del simulatore: in LTSpice il led simulato ha una tensione piu` bassa di quanto dichiarato dal data sheet. La tensione su ogni diodo con $20\,\text{mA}$ di corrente e` di soli $3.3\,\text{V}$ al posto dei $3.6\,\text{V}$ dichiarati dal data sheet.

Il conclusione si puo` dire: CLOSE ENOUGH!

Considerazioni

Per realizzare questo circuito bisogna ancora scegliere la topologia, il resistore e i diodi.

Per i diodi la scelta e` facile: la corrente media nel carico e` di $20\,\text{mA}$ e quindi quella media in ciascun diodo e` la meta`, $\overline{I_D}=10\,\text{mA}$ , e la tensione inversa che ogni diodo deve poter sopportare, in condizioni normali, e` di $325\,\text{V}$ piu` la tolleranza della rete. In pratica serve almeno un diodo da $400\,\text{V}$ , e visto che i diodi da $1000\,\text{V}$ e $1\,\text{A}$ sono comunissimi, giusto per non fare nomi 1N4007, mi pare sia una buona scelta prendere questi diodi.

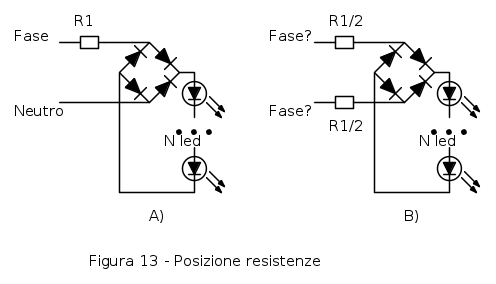
Il problema e` sulla scelta della resistenza e della topologia. Come gia` detto la variante di figura 5 C) e` da evitare. La ragione e` nella scarsa protezione dei diodi del ponte dalle sovratensioni di rete. Infatti in caso di sovratensione di rete la resistenza $R_1\,$ la assorbe, ma i diodi raddrizzatore la ricevono completamente, con possibili rotture.

Invece i circuiti A) e B) in caso di sovratensione di rete la assorbono sempre con la resistenza, ma la tensione sul ponte raddrizzatore e` limitata dalla resistenza posta in serie prima del ponte: in pratica i diodi vedono come tensione inversa solo quella dei led.

La scelta fra la versione A) e la versione B) riguarda la possibilita` di avere un contatto diretto della catena verso terra. Se fosse possibile garantire che la fase sia sempre collegata sul lato in cui c'e` la resistenza di protezione, come nella figura seguente A) la soluzione migliore sarebbe appunto la A).

Sorgente FidoCadJ | Ingrandisci | Cos'è Fidocad

Il questo modo si minimizzerebbe la corrente in caso di cortocircuito netto della stringa verso terra. Nel caso peggiore, dipendente da dove si verifica il guasto verso terra, la corrente di picco massima sarebbe di $80\,\text{mA}$ circa, con alcuni led piu` accesi di altri, ma tutti i led sopravviverebbero al guasto. In condizioni di guasto a terra, se non intervenisse una protezione differenziale, la resistenza $R_1\,$ dissiperebbe circa $8\,\text{W}$ .

In Italia (e molti altri stati) la distribuzione in alternata non ha prese e spine polarizzate per distinguere fase da neutro, e se si vuole proteggere il sistema da guasto diretto verso terra, e` necessario andare sullo schema di figura B), dove ciascuna delle due resistenze ha un valore dimezzato rispetto alla resistenza singola e dissipa anche meta` potenza del caso con una sola resistenza.

in questo caso a seconda di dove si localizza il guasto alcuni, led potrebbero subire uno stress di corrente media di circa $50\,\text{mA}$ , una delle due resistenze $\frac{R_1}{2}$ si troverebbe a dissipare oltre $15\,\text{W}$ , e potrebbe funzionare da protezione, aprendosi, sempre che non intervenga prima il differenziale.

In condizioni normali l'uso di due resistenze distribuisce anche la potenza dissipata: le due resistenze risultano essere da $2.2\,\text{k}\Omega$ oppure una da $2.2\,\text{k}\Omega$ e l'altra da $2\,\text{k}\Omega$ e dissippano ciascuna circa $1.6\,\text{W}$

Da notare che questi circuiti devono essere protetti da interruttore differenziale, far fuori Babbo Natale non mi pare una buona idea!

Surge

Infine e` di fondamentale importanza garantire la sopravvivenza del circuito a sovratensioni di rete, causate da manovre sulla rete o piu` spesso da fulmini. Le sovratensioni a cui puo` andare incontro il circuito sono normalizzate dalla IEC nella norma EN61000-5-4, e sono generate nelle prove di laboratorio con appositi strumenti, il cui circuito puo` essere usato in fase di simulazione per vedere come si comporta il circuito progettato.

Mentre la normativa prevede sia i test di tensione di modo differenziale che di modo comune, vengono simulati solo quelli di modo differenziale poiche' i voltage surge di modo comune interessano principalmente l'isolamento del circuito.

Il circuito che permette di simulare il surge differenziale con ampiezza di $1\,\text{kV}$ , tratto da [8] e` nella figura 14:

Figura 14 - Circuito per VOLTAGE SURGE

Il condensatore $C_2=18\,\mu\text{F}$ e l'induttore $L_5=1.5\,\text{mH}$ costituiscono la rete standard di accoppiamento del disturbo. La corrente attraverso i led e la tensione totale sulla catena di 40 led sono mostrate nella figura seguente:

Figura 15 - Simulazione VOLTAGE SURGE

Si vede che la corrente di picco sale fino a $270\,\text{mA}$ circa mentre la tensione su tutta la catena di led, e quindi anche la tensione inversa sui diodi, rimane limitata a circa $200\,\text{V}$ . La corrente di picco attraverso i led e` decisamente piu` elevata di quanto ammette il costruttore( $100\,\text{mA}$ ) e per avere un sistema affidabile e` necessario inserire all'ingresso un limitatore di sovratensioni: la scelta migliore e` un TVS (transient voltage suppressor) bidirezionale con una tensione di lavoro di $380\text{V}\,$ . Scelta meno buona potrebbe essere un varistore a ossidi metallici (MOV).