Indice |
La riduzione, o minimizzazione, delle funzioni booleane (quarta parte)
Era mia intenzione trattare il seguente argomento quando se ne fosse presentata l'opportunità durante l'illustrazione del funzionamento di alcuni circuiti di logica combinatoria (soprattutto nei decodificatori), ma poi ho ritenuto più opportuno, per non disperdere troppo la teoria, di inserire questo capitolo come "addendum" nella serie sulla riduzione delle funzioni booleane.
Le condizioni indifferenza (o don't care)
Negli ultimi tre articoli (LogicBignami (VI), LogicBignami (VII) e LogicBignami (VIII)) abbiamo visto tre metodi che ci permettono di attuare la riduzione di una funzione booleana in formato canonico.
Fino ad ora abbiamo considerato tabelle della verità in cui gli stati logici relativi alla funzione booleana d'uscita erano o a  logico (stato logico "falso") o a
logico (stato logico "falso") o a  logico (stato logico "vero").
logico (stato logico "vero").
Nella realtà vedremo che esistono dei casi che, per una o più combinazioni delle variabili booleane d'ingresso, lo stato logico della funzione booleana d'uscita non abbia importanza: essa potrebbe essere considerata indifferentemente a stato logico  o a stato logico
o a stato logico  , da cui il nome di condizione d'indifferenza o don't care condition.
, da cui il nome di condizione d'indifferenza o don't care condition.
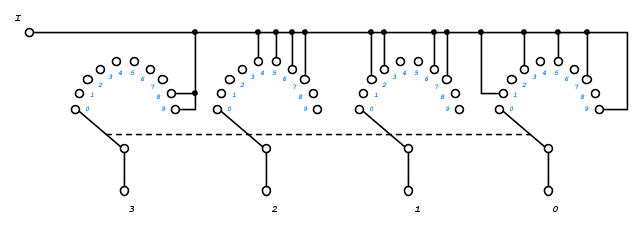
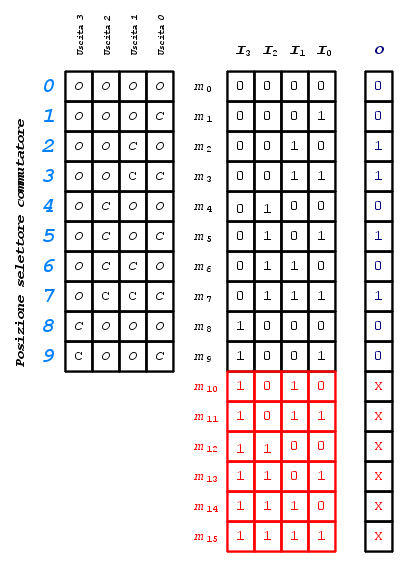
Supponiamo di avere un commutatore a dieci posizioni con  sezioni e
sezioni e  uscite, con interruttori che chiudono sull'ingresso
uscite, con interruttori che chiudono sull'ingresso  seguendo lo schema qui sotto riportato:
seguendo lo schema qui sotto riportato:
Questo tipo di commutatore, in pratica, permette la conversione delle cifre decimali da  a
a  , interpretate dalla posizione del contatto di commutazione, con le corrispondenti prime
, interpretate dalla posizione del contatto di commutazione, con le corrispondenti prime  combinazioni ottenibili con
combinazioni ottenibili con  variabili booleane (analizzeremo nei prossimi articoli i sistemi numerici e la conversione da uno all'altro sistema).
variabili booleane (analizzeremo nei prossimi articoli i sistemi numerici e la conversione da uno all'altro sistema).
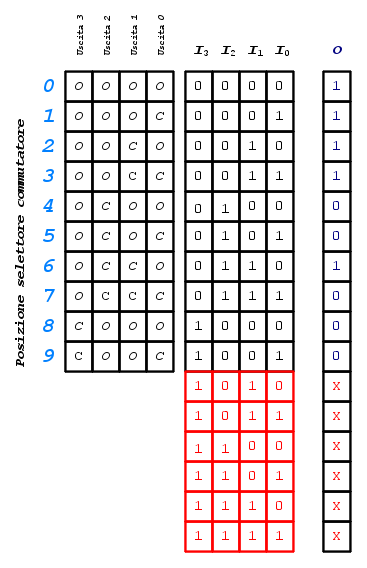
Se associassimo la lettera  per indicare il contatto aperto e la lettera
per indicare il contatto aperto e la lettera  per indicare il contatto chiuso, rispetto all'ingresso
per indicare il contatto chiuso, rispetto all'ingresso  , otterremo la seguente tabella (a sinistra) che, come si può notare, risulta identica alla prima parte della tabella della verità per
, otterremo la seguente tabella (a sinistra) che, come si può notare, risulta identica alla prima parte della tabella della verità per  variabili booleane (a destra) se considerassimo
variabili booleane (a destra) se considerassimo  come stato logico
come stato logico  e
e  come stato logico
come stato logico  :
:
Però sappiamo che, per  variabili booleane, si ottengono
variabili booleane, si ottengono  combinazioni diverse, quindi le prime
combinazioni diverse, quindi le prime  corrispondono alle posizioni del commutatore ma le restanti
corrispondono alle posizioni del commutatore ma le restanti  rimarrebbero inutilizzate (evidenziate in rosso nella tabella della verità qui sopra).
rimarrebbero inutilizzate (evidenziate in rosso nella tabella della verità qui sopra).
Quindi, in questo caso, in corrispondenza di queste combinazioni, non potendo mai capitare (gli stati di commutazione non le comprendono), lo stato logico assunto dalla funzione booleana d'uscita può essere, indifferentemente,  oppure
oppure  .
.
Per identificare lo stato logico di indifferenza, di norma, in corrispondenza di queste combinazioni delle variabili booleane d'ingresso, la funzione booleana d'uscita viene contrassegnata con la lettera  .
.
Questi stati logici indifferenza verranno considerati come stato logico  o come stato logico
o come stato logico  a seconda di come decideremo di esprimere la nostra funzione booleana d'uscita in formato canonico:
a seconda di come decideremo di esprimere la nostra funzione booleana d'uscita in formato canonico:
- Se intendiamo esprimerla come somma logica di prodotti logici, cioè come somma logica di mintermini, gli stati logici indifferenza saranno considerati come  logico e le relative combinazioni di variabili booleane d'ingresso, come mintermini.
logico e le relative combinazioni di variabili booleane d'ingresso, come mintermini.
- Se intendiamo, invece, esprimerla come prodotto logico di somme logiche, cioè come prodotto logico di maxtermini, gli stati logici indifferenza saranno considerati come  logico e le relative combinazioni di variabili booleane d'ingresso, come maxtermini .
logico e le relative combinazioni di variabili booleane d'ingresso, come maxtermini .
Da notare, però, che non è detto che tutti gli stati logici indifferenza presenti in una tabella della verità concorrano ad una maggior riduzione della funzione booleana d'uscita, quindi non è detto che tutti i mintermini (o maxitermini) ad essi corrispondenti debbano essere considerati durante il processo di riduzione.
Di seguito vedremo come utilizzare gli stati logici indifferenza nei tre sistemi di riduzione di una funzione booleana già analizzati: metodo algebrico, metodo delle mappe di Karnaugh e metodo Quine - McCluskey.
Gli stati logici indifferenza: il metodo "algebrico"
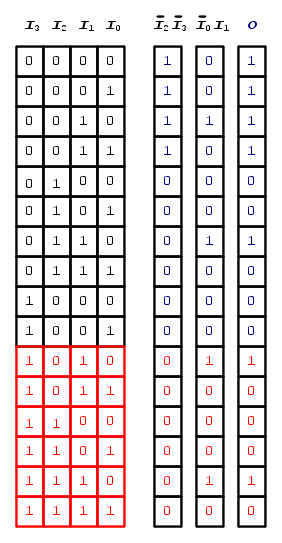
Consideriamo il caso in cui la nostra funzione booleana d'uscita  sia in stato logico
sia in stato logico  quando la posizione assunta dal selettore del commutatore appena visto si trova sui numeri
quando la posizione assunta dal selettore del commutatore appena visto si trova sui numeri  .
.
In tal caso otteniamo la seguente tabella della verità:
Consideriamo di realizzare la nostra funzione booleana d'uscita  come somma logica di prodotti logici, quindi come somma logica di mintermini e, per vedere quale vantaggio porta, alla riduzione della stessa, l'eventuale utilizzo delle condizioni di indifferenza come stato logico
come somma logica di prodotti logici, quindi come somma logica di mintermini e, per vedere quale vantaggio porta, alla riduzione della stessa, l'eventuale utilizzo delle condizioni di indifferenza come stato logico  , iniziamo a vedere come sarebbe se queste stesse condizioni indifferenti fossero ininfluenti per una funzione booleana somma logica di mintermini, quindi in stato logico
, iniziamo a vedere come sarebbe se queste stesse condizioni indifferenti fossero ininfluenti per una funzione booleana somma logica di mintermini, quindi in stato logico  :
:

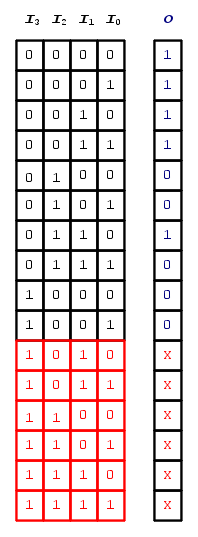
Procedendo come abbiamo già visto in LogicBignami (VI), passiamo alla riduzione per via algebrica, cercando il numero minimo di coppie di mintermini, che mi permettano di ridurre, se possibile, tutti i mintermini presenti, alle quali sia possibile applicare, in sequenza, la proprietà distributiva, la regola della complementarietà e la regola dell'elemento neutro (più la regola dell'idempotenza al mitermine  ): queste sono
): queste sono ![[m_0, \; m_1] \; \; [m_2, \; m_3] \; , \; [m_2, \; m_6] \;](/mediawiki/images/math/2/0/1/201572c030ce1f4250e92541d4ea9129.png) .
.
Stabilite le coppie di mintermini su cui agire si ottengono i seguenti implicanti:



si nota, altresì, che, i primi due imlòicanti trovati, sono ulteriormente riducibili:

Quindi, la nostra funzione booleana ridotta, senza considerare i termini di indifferenza, equivale a:

Siamo quindi passati dalla funzione booleana, in formato canonico, costituita dalla somma logica di  mintermini, ad una funzione booleana, in formato ridotto, costituita dalla somma logica di
mintermini, ad una funzione booleana, in formato ridotto, costituita dalla somma logica di  implicanti, uno costituito dal prodotto logico di
implicanti, uno costituito dal prodotto logico di  variabili booleane d'ingresso e l'altro dal prodotto logico di
variabili booleane d'ingresso e l'altro dal prodotto logico di  .
.
Vediamo allora se, l'inserimento, nella funzione booleana in formato canonico, delle condizioni di indifferenza come stato logico  , ci permette di ottenere una funzione booleana maggiormente ridotta.
, ci permette di ottenere una funzione booleana maggiormente ridotta.
Iniziamo considerando tutte le condizioni di indifferenza allo stato logico  e ricaviamo la nuova funzione booleana in formato canonico (di seguito il mintermine sottolineato indicherà che lo stesso deriva da una condizione di indifferenza):
e ricaviamo la nuova funzione booleana in formato canonico (di seguito il mintermine sottolineato indicherà che lo stesso deriva da una condizione di indifferenza):



Ora dobbiamo cercare, se esistono, quali mintermini, tra quelli risultanti dalle condizioni di indifferenza, ci permettono di ridurre ulteriormente i due implicanti  e
e  trovati in precedenza.
trovati in precedenza.
Innanzi tutto notiamo che nessuno dei mintermini derivati dalle condizioni di indifferenza permette di ricavare un implicante che possa ridurre  tipo
tipo  o
o  : infatti solo
: infatti solo  (la coppia
(la coppia ![[m_{10}, \; m_{11}] \;](/mediawiki/images/math/c/0/f/c0fd122f85be711ae6e9fd1d4bdf1609.png) ) contengono il gruppo di variabili
) contengono il gruppo di variabili  , da cui si otterrebbe l'unico implicante:
, da cui si otterrebbe l'unico implicante:

di nessuna utilità.
Vediamo, allora, se esiste la possibilità di ridurre l'implicante  .
.
Nessuno dei  mintermini derivati dalle condizioni di indifferenza contiene la variabile booleana
mintermini derivati dalle condizioni di indifferenza contiene la variabile booleana  quindi è logico suppore che, se sarà possibile, la riduzione porterà proprio all'eliminazione di questa variabile booleana.
quindi è logico suppore che, se sarà possibile, la riduzione porterà proprio all'eliminazione di questa variabile booleana.
Elenchiamo, allora, tutti i mintermini che contengono il gruppo di variabili booleane  , evidenziando sempre con una sottolineatura quelli derivanti dalle condizioni di indifferenza:
, evidenziando sempre con una sottolineatura quelli derivanti dalle condizioni di indifferenza:




Come sappiamo la riduzione della coppia ![[m_2, \; m_6] \;](/mediawiki/images/math/f/4/a/f4aa86e778480e40d2ebbb0ba4aa1f55.png) da limplicante
da limplicante  , mentre dalla coppia
, mentre dalla coppia ![[m_{10}, \; m_{14}] \;](/mediawiki/images/math/5/1/0/51003dd090fb7139bf5ada9f97434116.png) risulta limplicante:
risulta limplicante:

a loro volta, questi due implicanti sono, tra loro, riducibili

Anche per questo implicante non esiste possibilità di ulteriori riduzioni, con i mintermini a disposizione, quindi, di tutti quelli derivati dalle condizioni di indifferenza, gli unici utili per ridurre ulteriormente la nostra funzione booleana sono esclusivamente  e
e  :
:


Come riprova ricaviamoci la relativa tabella della verità:
Come si vede gli stati logici assunti dalla funzione booleana  sono identici a quelli presenti nella tabella della verità di inizio paragrafo, le condizioni di indifferenza hanno, ovviamente assunto gli stati logici coerenti con le scelte fatte in fase di riduzione ma, come tali, non sono di alcuna importanza per la funzionalità richiesta.
sono identici a quelli presenti nella tabella della verità di inizio paragrafo, le condizioni di indifferenza hanno, ovviamente assunto gli stati logici coerenti con le scelte fatte in fase di riduzione ma, come tali, non sono di alcuna importanza per la funzionalità richiesta.
Gli stati logici indifferenza: il metodo delle "mappe di Karnaugh"
Abbiamo appena visto che l'analisi per la scelta di quanti e quali condizioni indifferenza utilizzare mediante la riduzione con il metodo algebrico può risultare relativamente lunga e complessa, cosa soprattutto vera all'aumentare del numero di variabili booleane manipolate.
Con il metodo delle mappe di Karnaugh, invece, l'operazione di selezione e scelta delle condizioni di indifferenza risulta la più semplice e immediata, con il limite, però, come già detto in articoli precedenti, che, di fatto, è praticabile solo per sistemi che utilizzano, al massimo,  variabili booleane.
variabili booleane.
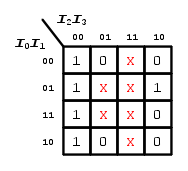
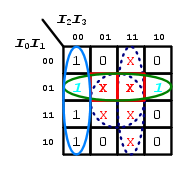
Vediamo, allora, come sarebbe stata più veloce la semplificazione della funzione booleana relativa all'uscita  della tabella della verità usata nel paragrafo precedente:
della tabella della verità usata nel paragrafo precedente:
Da questa si ricava, come abbiamo visto nell'articolo LogicBignami (VII), la seguente mappa di Karnaugh:
Consideriamo, anche qui, di voler ottenere una funzione booleana come somma logica di prodotti logici, quindi utilizzaremo i mintermini in stato logico  escludendo, per il momento, le condizioni di indifferenza per meglio esplicitare il loro contributo alla riduzione della funzione booleana d'uscita.
escludendo, per il momento, le condizioni di indifferenza per meglio esplicitare il loro contributo alla riduzione della funzione booleana d'uscita.
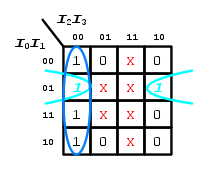
Vediamo, allora, che sono possibili due soli raggruppamenti: uno da  mintermini (indicato in blu) e uno da
mintermini (indicato in blu) e uno da  (indicato in azzurro).
(indicato in azzurro).
Da questi due raggruppamenti, considerando in ognuno le variabili booleane che non cambiano di stato logico, si ricava la fuznione booleana:

Dobbiamo ora vedere se, tra le condizioni di indifferenza, ci sono dei termini che, considerati in stato logico  , permetterebbero di eseguire dei raggruppamenti con un meggior numero di mintermini rispetto ai precedenti inglobando i termini già in stato logico
, permetterebbero di eseguire dei raggruppamenti con un meggior numero di mintermini rispetto ai precedenti inglobando i termini già in stato logico  .
.
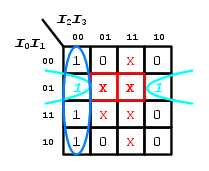
Dalla disposizione delle  sulla mappa di Karnaugh si nota che solo due di queste, evidenziate con riquadri in rosso, permetterebbero di avere un raggruppamento da
sulla mappa di Karnaugh si nota che solo due di queste, evidenziate con riquadri in rosso, permetterebbero di avere un raggruppamento da  mintermini (evidenziato in verde), andando ad inglobare il raggruppamento da
mintermini (evidenziato in verde), andando ad inglobare il raggruppamento da  precedente:
precedente:
Quindi, la funzione booleana definitivamente ridotta, con il contributo delle condizioni di indifferenza, risulterà essere:

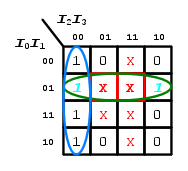
E' da tener presente che, quando, in una mappa di Karnaugh, sono presenti delle condizioni di indifferenza queste vanno considerate solo se sono utili, cioè solo se permettono di incorporare mintermini già in stato logico  (quelli, cioè, che sono già in uno stato logico prestabilito dalla funzione booleana richiesta) in raggruppamenti più grossi di quelli realizzabili senza condizioni di indifferenza.
(quelli, cioè, che sono già in uno stato logico prestabilito dalla funzione booleana richiesta) in raggruppamenti più grossi di quelli realizzabili senza condizioni di indifferenza.
Nella nostra mappa di Karnaugh, ad esempio, si nota che sarebbero possibili altri due raggruppamenti da  mintermini, segnati con il tratteggio: questi sono inutili perchè incorporano esclusivamente delle condizioni di indifferenza non portando, quindi, a nessuna ulteriore semplificazione alla nostra funzione booleana.
mintermini, segnati con il tratteggio: questi sono inutili perchè incorporano esclusivamente delle condizioni di indifferenza non portando, quindi, a nessuna ulteriore semplificazione alla nostra funzione booleana.
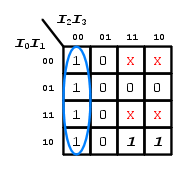
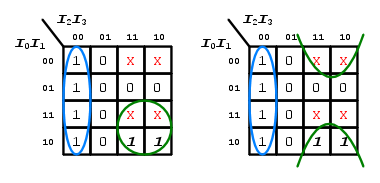
Come abbiamo già visto nell'articolo dedicato alla semplificazione tramite le mappe di Karnaugh, anche in presenza di condizioni di indifferenza potrebbe capitare una situazione che ammette più soluzioni equivalenti.
Consideriamo, ad esempio, la seguente mappa di Karnaugh:
Come si può notare i due mintermini evidenziati in grassetto potrebbero essere raggruppati in due modi con altrettante due condizioni di indifferenza:
Queste, ai fini della semplificazione, sono identiche, per tanto se ne sceglierà una delle due a prorpia discrezione.
Vista l'applicazione delle condizioni di indifferenza anche al metodo delle mappe di Karnaugh, passiamo adesso ad analizzare il loro impiego con il metodo di riduzione Quine-McCluskey
Gli stati logici indifferenza: il metodo "Quine-McCluskey"
Per vedere come utilizzare le condizioni di indifferenza nella riduzione delle funzioni booleane con il metodo Quine-McCluskey, partiamo sempre da un esempio con il nostro commutatore di inizio articolo.
Questa volta supponiamo che la funzione booleana dell'uscita  , di nostro interesse, sia a livello logico
, di nostro interesse, sia a livello logico  quando il selettore del commutatore sia posizionato in corrispondenza di un numero primo, quindi in corrispondenza dei numeri
quando il selettore del commutatore sia posizionato in corrispondenza di un numero primo, quindi in corrispondenza dei numeri  , per cui ricaviamo la seguente tabella della verità:
, per cui ricaviamo la seguente tabella della verità:
A questo punto dobbiamo procedere come abbiamo visto nell'articolo LogicBignami (VIII) per eseguire riduzione secondo il metodo Quine-McCluskey.
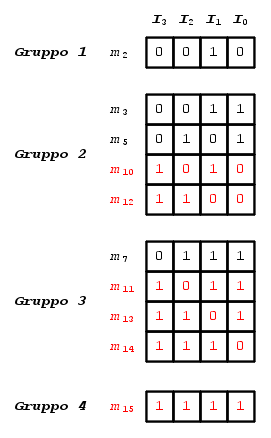
Innanzi tutto ricaviamo la tabella dove raggruppiamo i mintermini relaitivi allo stato logico  della funzione booleana d'uscita, suddivisi secondo il numero delle corrispondenti variabili booleane d'ingresso settate a livello logico
della funzione booleana d'uscita, suddivisi secondo il numero delle corrispondenti variabili booleane d'ingresso settate a livello logico  (gruppo 1, una sola variabile booleana a livello logico
(gruppo 1, una sola variabile booleana a livello logico  - gruppo 2, due variabili booleane a livello logico
- gruppo 2, due variabili booleane a livello logico  , ... ) : in questi gruppi inseriremo anche tutti i mintermini relativi alle condizioni di indifferenza
, ... ) : in questi gruppi inseriremo anche tutti i mintermini relativi alle condizioni di indifferenza  che, di conseguenza, considereremo allo stato logico
che, di conseguenza, considereremo allo stato logico  :
:
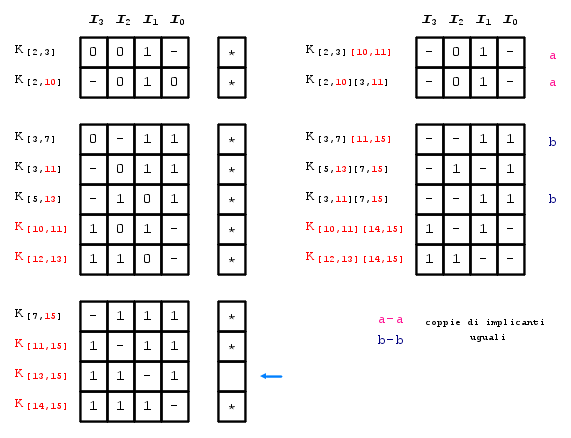
Iniziamo, quindi, a cercare gli implicanti primi ![K_{[n, \; m] \; [p, \; q]...} \;](/mediawiki/images/math/0/f/0/0f0660d442d862c0f64bc1652bfe15fd.png) , ricavando la tabella, innanzi tutto, degli implicanti che derivano dalla riduzione dei mintermini (ricordo che la colonna con il carattere "*" ci serve per vedere se non è stato possibile ridurre qualche termine):
, ricavando la tabella, innanzi tutto, degli implicanti che derivano dalla riduzione dei mintermini (ricordo che la colonna con il carattere "*" ci serve per vedere se non è stato possibile ridurre qualche termine):
Proseguiamo, cercando ulteriori riduzioni tra gli implicanti appena trovati, ricavando questa utletriore tabella:
Notiamo che nella tabella di sinistra l'implicante ![K_{[13, \; 15]} \;](/mediawiki/images/math/a/1/f/a1f89e25a09a2d802e73126dce4c8099.png) , indicato con la freccia blu, non è stato possibile sommarlo logicamente con nessuno del gruppo precedente al fine di ridurlo, quindi sarebbe un implicante primo: in realtà, essendo il risultato, a sua volta, della somma logica di due mintermini derivati da condizioni di indifferenza, questo non rientrerà nel grafico degli implicanti primi.
, indicato con la freccia blu, non è stato possibile sommarlo logicamente con nessuno del gruppo precedente al fine di ridurlo, quindi sarebbe un implicante primo: in realtà, essendo il risultato, a sua volta, della somma logica di due mintermini derivati da condizioni di indifferenza, questo non rientrerà nel grafico degli implicanti primi.
Nella tabella di destra, invece, si nota che:
1) La presenza di due coppie di implicanti uguali, la coppia indicata dalla lettera "a" e quella indicata dalla lettera "b": di ognuna di queste si utilizzerà un unico implicante.
2) Nessun implicante del gruppo superiore può essere accoppiato (sommato logicamente al fine di ridurlo) con un implicante del gruppo inferiore, quindi, ogni implicante, è un implicante primo, però, anche in questa tabella sono presenti due implicanti, ![K_{[10, \; 11] \; [14, \; 15]} \;](/mediawiki/images/math/c/c/e/cce5cd828a392d2f279df580ddad80f1.png) e
e ![K_{[12, \; 13] \; [14, \; 15]} \;](/mediawiki/images/math/a/6/7/a679e6e14c4dc9ace604ffd5c8bdb640.png) , che sono il risultato della riduzione di mintermini derivati da condizioni di indifferenza che, pertanto, non saranno inseriti, neanche loro, nel grafico degli implicanti primi.
, che sono il risultato della riduzione di mintermini derivati da condizioni di indifferenza che, pertanto, non saranno inseriti, neanche loro, nel grafico degli implicanti primi.
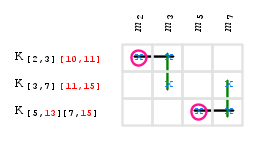
Fatte queste considerazioni possiamo costruire il grafico degli implicanti primi dove non compariranno, come indicizzazione delle colonne, i mintermini derivati dalle condizioni di indifferenza:
Come possiamo vedere sono presenti due colonne, rispettivamente indicizzate da  e
e  , che contengono un unico carattere "x" (evidenziato in un cerchio): come sappiamo, gli implicanti primi in corispondenza di questi diventano implicanti primi essenziali e finiscono direttamente nella funzione booleana ridotta.
, che contengono un unico carattere "x" (evidenziato in un cerchio): come sappiamo, gli implicanti primi in corispondenza di questi diventano implicanti primi essenziali e finiscono direttamente nella funzione booleana ridotta.
Tutti i caratteri "x" sulla medesima riga degli implicanti primi essenziali vanno cancellati, così come tutti i caratteri "x" presenti nelle colonne corrispondenti a tutte le precedenti "x" cancellate, ricavando il seguente grafico:
Come si vede i soli due implicanti primi essenziali bastano a coprire tutti gli stati logici  dei mintermini realtivi alla funzione booleana richiesta, pertanto la stessa equivarrà alla somma logica dei due:
dei mintermini realtivi alla funzione booleana richiesta, pertanto la stessa equivarrà alla somma logica dei due:
![O = K_{[2, \; 3] \; [10, \; 11]} + K_{[5, \; 13] \; [7, \; 15]} = I_1 \; \overline {I_2} + I_0 \; I_2](/mediawiki/images/math/e/6/2/e620743e834eaeef4ad07088c0d05913.png)
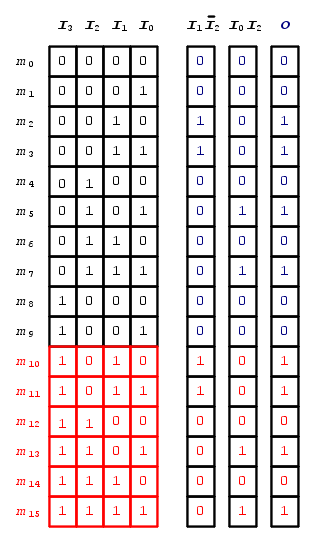
A riprova che sia la funzione booleana richiesta, possiamo ricavarci la relativa tabella della verità:
Come volevasi dimostrare gli stati logici della funzione booleana d'uscita  sono identici a quelli della tabella della verità di inizio paragrafo.
sono identici a quelli della tabella della verità di inizio paragrafo.
Da questa tabella della verità si nota anche che le uniche condizioni di indifferenza, che vanno considerate a stato logico  , necessarie per la riduzione della funzione booleana, sono quelle relative ai mintermini
, necessarie per la riduzione della funzione booleana, sono quelle relative ai mintermini  ,
,  ,
,  e m15 che sono poi quelli "manipolati" nei due implicanti primi essenziali.
e m15 che sono poi quelli "manipolati" nei due implicanti primi essenziali.
Con questo abbiamo terminato questo addendum relativo all'utilizzo delle condizioni di indifferenza nella riduzione delle funzioni booleane, questo, come abbiamo detto ad inizio articolo, ci tornerà sicuramente utile in prossimi quando analizzeremo la realizzazione dei circuiti digitali di decodifica.

 Elettrotecnica e non solo (admin)
Elettrotecnica e non solo (admin) Un gatto tra gli elettroni (IsidoroKZ)
Un gatto tra gli elettroni (IsidoroKZ) Esperienza e simulazioni (g.schgor)
Esperienza e simulazioni (g.schgor) Moleskine di un idraulico (RenzoDF)
Moleskine di un idraulico (RenzoDF) Il Blog di ElectroYou (webmaster)
Il Blog di ElectroYou (webmaster) Idee microcontrollate (TardoFreak)
Idee microcontrollate (TardoFreak) PICcoli grandi PICMicro (Paolino)
PICcoli grandi PICMicro (Paolino) Il blog elettrico di carloc (carloc)
Il blog elettrico di carloc (carloc) DirtEYblooog (dirtydeeds)
DirtEYblooog (dirtydeeds) Di tutto... un po' (jordan20)
Di tutto... un po' (jordan20) AK47 (lillo)
AK47 (lillo) Esperienze elettroniche (marco438)
Esperienze elettroniche (marco438) Telecomunicazioni musicali (clavicordo)
Telecomunicazioni musicali (clavicordo) Automazione ed Elettronica (gustavo)
Automazione ed Elettronica (gustavo) Direttive per la sicurezza (ErnestoCappelletti)
Direttive per la sicurezza (ErnestoCappelletti) EYnfo dall'Alaska (mir)
EYnfo dall'Alaska (mir) Apriamo il quadro! (attilio)
Apriamo il quadro! (attilio) H7-25 (asdf)
H7-25 (asdf) Passione Elettrica (massimob)
Passione Elettrica (massimob) Elettroni a spasso (guidob)
Elettroni a spasso (guidob) Bloguerra (guerra)
Bloguerra (guerra)




 ..
..  ..
..